Статья опубликована в авторской редакции. Мнение редакции не всегда совпадает с авторской линией. Но редакция всегда открыта к диалогу и предоставляет специалистам возможность донести свою идею до читательской аудитории журнала. Специализированный журнал – это информационная площадка, на которой порой встречаются самые невероятные инженерные решения и проявления творческой мысли.
Хроническое увлечение воспроизводством зарубежных технологий в электронике и радиофизике с точки зрения национальной безопасности, в конечном счёте, может привести к национальной катастрофе [1]. В ближайшие 2–3 года ведущие мировые технологические площадки в США (как минимум, две), в Бельгии и Корее преодолеют своего рода «сверхзвуковой барьер» в энергетике на твёрдых кристаллах, связанный с освоением топологической наноразмерности в 4–5 нм. Основанием для такого утверждения служит то, что недавно компания IBM объявила о создании первых рабочих образцов процессоров с транзисторами размером 7 нм [2]. Тогда что можно говорить о чипах отечественного производства с размерностью в 95 нанометров?
К 2025 г. западные компании вплотную приблизятся к молекулярной субнано-твёрдотельной электронике и, в недалёком будущем, к атомной электронике. Это приведёт к созданию сверхтехнологий, позволяющих осуществлять модуляцию и управление энергиями в кристалле последовательно от единиц кэВ до сотен кэВ и выше (МэВ), что является предварительным шагом к сопоставимым величинам энергий (неуправляемых!) ядерного расщепления и термоядерного синтеза (зонная теория оперирует на практике энергиями от 0,17 эВ (InSb) до 5,5 эВ (Diamond), а плотность энергии формируется флюенсом проводящих электронов/дырок или фотонов).
Следует ожидать, что к 2020 г. будут освоены «транзисторно-диодные» операции усиления, генерации, модуляции (ЧМ, АМ, ФМ), Булевой логики в диапазоне частот 1012–1018 Гц. Следовательно, интеллектуальная планка любой нации определяется скоростью обработки информации, а также частотной энергоплотностью оперируемой электромагнитной массы.
При хроническом технологическом отставании от ведущих держав в области электроники, что мы можем противопоставить процессу брожения опасной идеи «безответного удара»? Тем более в условиях сверхвысокой технологической оснащённости для операций генерации и управления энергиями, близкими или сопоставимыми с ядерными?
Отсюда вывод: чтобы не пропустить момент, когда гром действительно грянет, необходимо практически в аварийном порядке изыскивать внутренние интеллектуальные ресурсы, которые в России – неисчерпаемы. Нужно твёрдо усвоить слова немецкого физика Роберта Кирхгофа: «Нет ничего практичнее хорошей теории».
В очередной публикации авторы вновь заостряют внимание на достоинствах своего проекта «Новая мировая электронная индустрия на основе LPE i-GaAs-монокристаллов опережающего уровня», тезисы которой были ими разосланы в ведущие концерны, РАН, ведущие вузы и другие организации.
Далее вкратце интерпретированы дополнительные возможности новых кристаллов в области релятивистской и фотонной сверхпроводимости.
Проводимость твёрдых тел
Исходя из свойств электрической проводимости в физике, принято делить твёрдые тела на проводники (ρ < 10–5 Ом × см), полупроводники (ρ = 109¼10–4 Ом × см) и диэлектрики (ρ > 109 Ом × см). О корректности такой трактовки проводимости в твёрдых телах можно судить хотя бы по тому, что:
- чистые, беспримесные, совершенные по своей структуре кристаллы алмаза и арсенида галлия являются ди-электриками с удельным сопротивлением гораздо выше, чем 109 Ом × см (количество свободных электронов – один на 10 000 триллионов атомов или меньше);
- легированные монокристаллы алмаза и арсенида галлия (GaAs) – это полупроводники со всеми вытекающими свойствами;
- финскими учёными продемонстрированы на практике GaAs-структуры с проводимостью на порядок и более высокой, чем в металлах (Ag, Au, Cu, Al и др.) [3];
- в статье «Новая экстремальная электроника на основе LPE i-GaAs-моно-кристаллов» [4] показано 5 последовательно-переходных типов проводимости в монокристаллах LPE i-GaAs – от диэлектрика до полупроводника/проводника и, в перспективе, сверхпроводника.
Естественно, возникает вопрос: в чем же, с физической точки зрения, заключается качественная разница проводимости, как характеристики передачи электромагнитной энергии в твёрдых телах?
Ответ заключается в скорости и способах переноса электромагнитной энергии. В области электроники, как правило, перенос или преобразование электромагнитной энергии связывают с зонной теорией проводимости (полупроводники) и релятивистским переносом энергии посредством заряженных частиц (вакуумные ускорители, циклотроны, изотопы и так далее, вплоть до термоядерного генератора – Солнца). Уместно и такое существенное замечание: в металлах подвижность электронов, которая характеризует дрейфовую скорость переноса электромагнитной энергии (при нормальных условиях), имеет сверхмалые величины, например, Ag – 56 cм2/В × с, Cu – 35 cм2/В × с, Al – 10 cм2/В × с, при практической напряжённости поля, не превышающей 0,001 В/см, то есть скорость потока электронов не выше, чем полмиллиметра в секунду (0,5 × 10–1 см/с), к примеру, в GaAs v = 2 × 107 см/с. Как же тогда понимать в отношении металлов выражение, что электрический ток – это направленное движение заряженных частиц? Направленного движения электрически заряженных частиц, тех же электронов, концентрация которых, допустим, в меди » 8 × 1022 см–3, практически нет. Есть дрейфово-тепловой, слегка упорядоченный хаос движения таких частиц. А вот такая характеристика проводимости, как скорость передачи/переноса электрической энергии, очень высока и достигает субзначений скорости света в вакууме С ≈ 3 × 1010 см/с. В металлах проводимость (передача/перенос) электромагнитной энергии обусловлена волновыми свойствами поляризованного взаимодействия атомов кристаллической решётки. В данном случае мы имеем дело с фотонной проводимостью.
Фотонная проводимость наиболее ярко проявляется в диэлектрической среде (вакуум, ионосфера, стратосфера, тропосфера, диэлектрические материалы с очень малыми значениями ε – диэлектрической проницаемости), менее удачно – в металлах, и совсем неплохо – в твёрдых телах, совмещающих в себе свойства изолятора, полупроводника, проводника, сверхпровод-ника (на примере того же алмаза или арсенида галлия).
Классическая зонная теория проводимости – это не что иное, как физическое явление ионизации атома или группы атомов полупроводника, связанное с процессом либо присоединения, либо отторжения заряженной частицы атома.
Рассматривая электрон как продукт ионизации, необходимо констатировать, что энергия ионизации атомов идеальной решётки известных полупроводников (Si, Ge, GaAs и других) колеблется в пределах 6–8 эВ, а точнее, у кремния (Si) – 8,1517 эВ, у германия (Ge) – 7,8995 эВ, мышьяка (As) – 9,789 эВ, галлия (Ga) – 5,999 эВ [6]. То есть энергия ионизации GaAs, вероятно, находится в пределах от 6,0 эВ.
Тем не менее, на практике мы оперируем оптической шириной запрещённой зоны в кремнии – 1,12 эВ или в GaAs – 1,43 эВ. Фактическое преобразование энергии ионизации GaAs в оптическую ширину запрещённой зоны с потерей ≈ 5 эВ так просто объяснить невозможно. К примеру, температурным фактором (тепловыми квантами – kT) здесь никакая экспонента
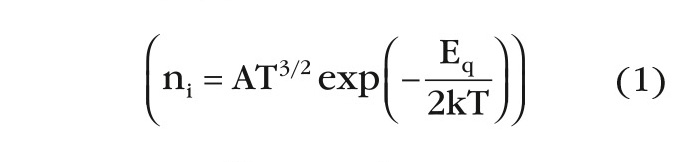
не поможет. Как в собственном полупроводнике кристалла GaAs «набрать» таким способом концентрацию свободных носителей ni = n = p → < 106 cм–3?
Очевидно, что снижению «термической» запрещённой зоны от 6–8 эВ до уровня «оптической» 1,12 эВ (Si) или 1,43 эВ (GaAs) способствуют структурные несовершенства кристалла и атмосфера (атомная среда), в которой выращиваются полупроводниковые кристаллы. Для изменения энергосостояния решётки кардинальным образом достаточно структурных несовершенств атомной решётки на уровне 10–9–10–10% атомной плотности кристалла.
Наряду со структурными методами влияния на энергию ионизации в кристаллической решётке полупроводника, практическим способом создания количества ионизированных состояний в решётке полупроводника является примесное легирование, которое, как известно, на практике используется в пределах 1013–1020 атомов/см3 (в кремнии, германии, арсениде галлия) или 10–4–10–11% плотности атомной упаковки. Полупроводниковые кристаллы, как правило, ионизированы уже при комнатной температуре из-за наличия в узлах кристаллической решётки донорной или акцепторной примесей. К примеру, энергия ионизации донорной примеси в Si, Ge, GaAs определяется по формуле:
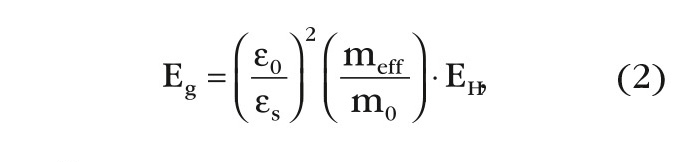
где EH – энергия ионизации атома водорода, равная 13,6 эВ, ε0 – диэлектрическая проницаемость вакуума, m0 и meff – масса покоя электрона и эффективная масса электрона (в зоне проводимости).
Энергия ионизации донорной примеси [6] в GaAs составляет 5–6 мэВ, акцепторной – 26–35 мэВ.
Формула (2) справедлива в общем случае, но есть полупроводниковые кристаллы AIIIBV, которые в случае легирования амфотерной примесью элементами IV группы таблицы Менделеева, например, при LPE-выращивании, могут противоречить формуле (1), и энергия ионизации может отличаться более чем на полтора порядка. Вследствие этого у LPE i-GaAs-кристалла, легированного кремнием в кварцевой среде («кварцевый» LPE i-GaAs), проявляются новые уникальные свойства по электропрочности, подвижности носителей заряда и политипу проводимости (от r > 109 Ом × см до идеальной, близкой к металлической, проводимости с r << 10–6 Ом × см).
Данный материал открывает новую страницу в современной электронике, на нём можно выполнить более широкий спектр приборов, чем на всех остальных полупроводниковых материалах вместе взятых.
Рассмотрим некоторые вопросы, связанные с электронной и релятивистской проводимостями в кристаллах LPE i-GaAs (Si/SiO2), но вначале рассмотрим энергетику LPE i-GaAs-монокристалла.
Энергетика GaAs монокристалла
Процессы и методы ионизации кристаллической структуры монокристаллов GaAs, то есть процессы, связанные с модуляцией проводимости GaAs, следующие:
1) технологические (ростовые, эпитаксиальные процессы, термообработка, легирование донорной или акцепторной примесью);Идеальный, беспримесный, бездефектный GaAs монокристалл в равновесном состоянии представляет собой чистый диэлектрик, в котором концентрация собственных носителей заряда находится на ничтожном вероятностном уровне меньше, чем 10–18% от плотности атомной упаковки.
2) полевые, то есть электромагнитные методы;
3) релятивистские (фотонные, электронные, протонные, нейтронные, гамма-лучевые и другие).
Энергетика реального «кварцевого» LPE i-GaAs-монокристалла, легированного амфотерными атомами кремния, резко отличается от классической интерпретации энергетики GaAs-монокристаллов [7], легированных акцепторной и донорной примесью, хотя бы из-за того, что атомы кремния в арсениде галлия во втором случае имеют энергию ионизации 0,035 и 0,005 эВ соответственно (мелкие уровни у краёв энергозон), а в LPE i-GaAs-амфотерный кремний образует глубокие, одновременно акцепторные и донорные уровни вблизи собственного электрохимического потенциала (EF). Механизм образования таких уровней находится в стадии исследования, но он связан с замещением атомами Si атомов Ga с дальнейшим атомным туннелированием в подрешётку мышьяка (As). На практике Войтовичем В.Е. и Ашкинази Г.А. [8, 9] получены практически «нулевые» разницы донорной и акцепторных примесей на уровне » 1011 см–3 при растворимости атомов Si в решётке GaAs в пределах осязаемости измерений от 1013 до 5 × 1016 см–3 атомов кремния в GaAs. Но необходимо также подчеркнуть, что легирование решётки GaAs атомами Si из фазы SiO происходит в результате образования как минимум четырёх глубоких центров:
- двух энергетически почти симметричных глубоких донорных и акцепторных центров;
- глубоких центров, образованных атомами кислорода (ниже середины запрещённой зоны);
- очень глубоких, с большой вероятностью, в валентной зоне акцепторных центров SiO в GaAs.
Исследования температурной зависимости параметров накопления и релаксации инжекционного заряда в p–i–n-структурах указывают на возрастание температурного фактора активации глубоких центров, начиная с температуры кристалла ≈ 220–250°С (высвобождение электронно-дырочных пар, вероятно, водородоподобного типа (экситонного типа) с образованием уровней в запрещённой зоне GaAs). Этим объясняется то обстоятельство, что глубокие центры усиливают свою электроактивность в виде скоростных рекомбинационных центров (постоянная решётки кремния всего на 4% отличается от постоянной решётки GaAs). В связи с этим, очевидно, происходит скоростной рекомбинационный процесс с туннельным обменом зарядов на симметричных глубоких центрах Si с решёткой GaAs. Одновременно параллельно происходит прямозонный переход электронов в валентную зону с квантовым инфраизлучением. На это косвенно указывает снижение объёмного p–i–n инжекционного заряда на 5–10% при температуре Tj ≥ 250°C (снижение времени восстановления обратного сопротивления p–i–n-структур), что не обнаружено в Si, SiC p–i–n и SBD-структурах (в Si p–i–n-структуре с ростом температуры заряд обратного восстановления утраивается (при Tj = 125–150°C)).
Возбуждение (некритическая ионизация) по водородоподобному типу фотонными импульсами со значениями меньше порога энергии ионизации амфотерных атомов кремния в решётке GaAs неизбежно приведёт к изменению диэлектрической проницаемости решётки LPE i-GaAs, легированного кремнием, с очень медленным ростом e до определённого критического уровня (≈ ≥1017 см–3 атомов кремния в GaAs), с дальнейшим резким значительным ростом e (см. рис. 1) предположительно в несколько раз, при инвертировании i-проводимости в n-тип, или, что более вероятно, при понижении температуры – в p-тип.
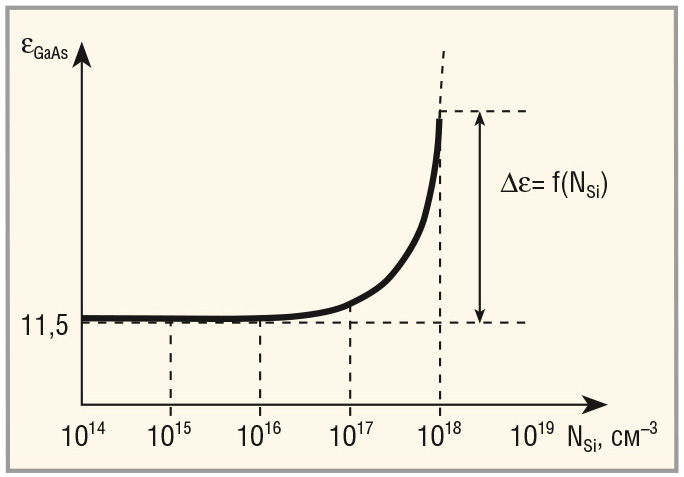
Таким образом, как приведённые практические данные, так и теоретические предположения совершенно очевидно ведут к новым качественным дополнениям в зонной теории проводимости полупроводников AIIIBV, легированных амфотерными примесями IV группы таблицы Менделеева в процессе LPE-выращивания.
Впервые эффект инвертирования собственной i-проводимости LPE GaAs («графитовый» метод выращивания), легированного амфотерными атомами германия, описан лауреатами Ленинской премии В.М. Андреевым, Л.М. Долгиновым и Д.Н. Третьяковым в монографии под редакцией лауреата Нобелевской премии Ж.И. Алфёрова «Жидкостная эпитаксия в технологии полупроводниковых приборов» [10]. В монографии показано инвертирование по типу i → n-тип на уровне ≥ 3 × 1017 см–3 атомов Ge в GaAs.
Амфотерность в GaAs также присутствует и при легировании атомами олова (в LPE-процессе выращивания). Амфотерность атомов IV группы Таблицы Менделеева проявляется и в таких соединениях AIIIBV, как InSb, GaSb, InAs и другие.
Энергетика реального монокристалла, выращенного методом жидкофазной (LPE) эпитаксии, легированного амфотерными атомами кремния (Si), синхронно замещающими атомы Ga и As в кристаллической решётке GaAs, показана на рисунке 2.
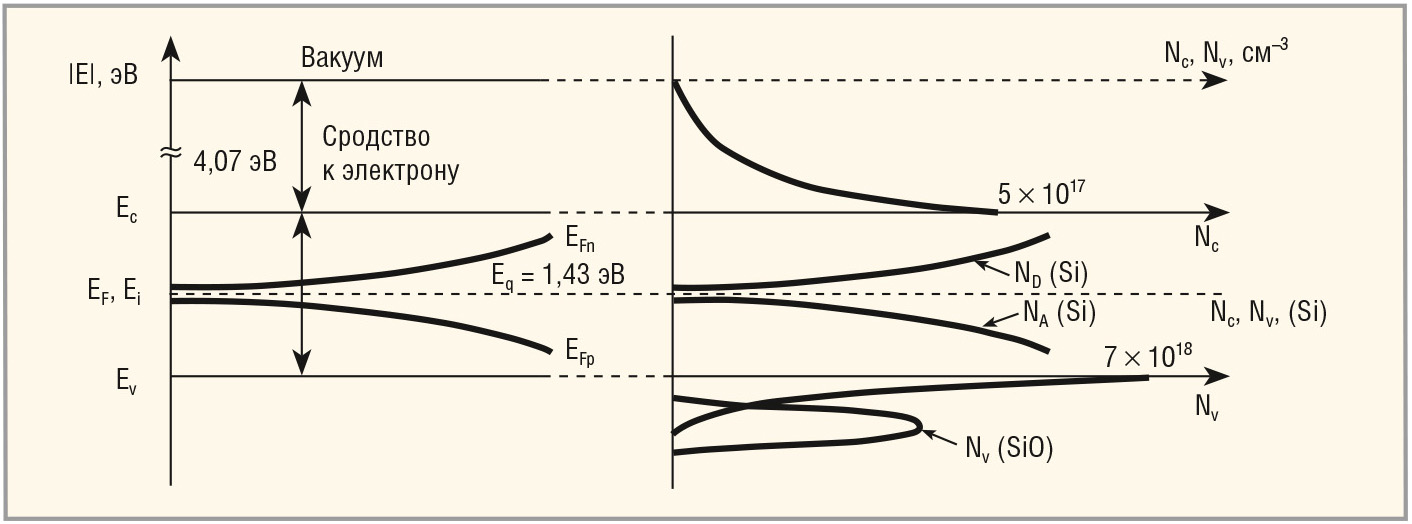
На рисунках 3 и 4 показана существенная качественная разница свойств полупроводниковых монокристаллов Si и LPE i-GaAs (Si – кварц).
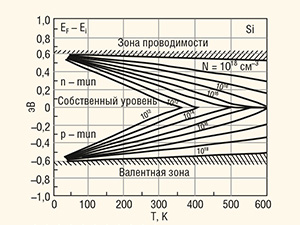
![Рис. 3. Зависимость уровня Ферми в кремнии от температуры и концентрации примесей и процесса сужения запрещённой зоны [7]](/images_soel/publications/2015/2015-7/СоЭл_2015-7pr_page15_pic3.jpg)
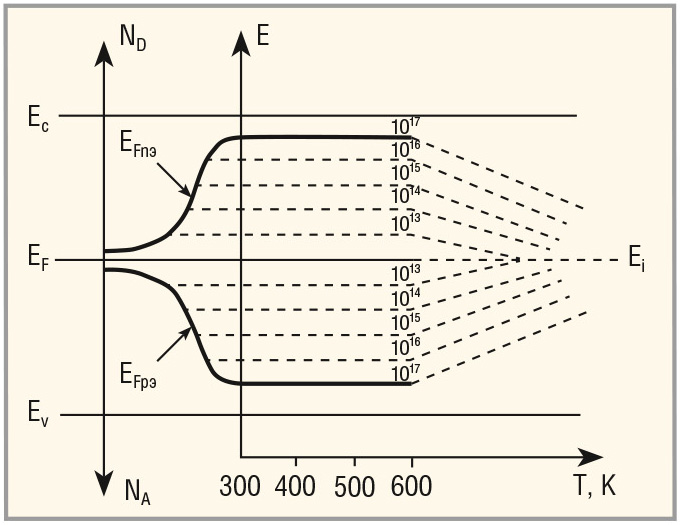
На основании оценки новых физических свойств LPE i-GaAs, показанных на рисунках 1, 2, 3 и 4, следует, что на основе свойств инвертирования i-проводимости в классическую примесную проводимость, практической независимости уровня Ферми от температуры в диапазоне 300–600 К, а также фактора зависимости ε = f(NA, ND)Si и резкого снижения энергии ионизации с ростом концентрации амфотерных атомов, возможно построение принципиально новых фотонных приборов с динамической проводимостью электромагнитной энергии со скоростями на 2–2,5 порядка выше, чем в классических полупроводниковых приборах и с более высокой энергоплотностью.
Электронная модель релятивистской проводимости
Такие фирмы, как IBM, а также Intel и Samsung, примерно к 2018 г. подготовят условия, когда зонную теорию проводимости ждёт участь «динозавров».
При длине дрейфового пролёта электрона в кристаллической решётке ионно-связанных материалов AIIIBV, таких как GaAs, InP, InSb, GaSb и другие, не более чем 45 Å или 4,5 нм, при приложении внешнего электрического поля носители заряда не будут испытывать рассеяния (то есть пролёт электронов не будет сопровождаться выделением джоулева тепла). Что это значит? Ток в теле GaAs не будет подчиняться основополагающей формуле зонной проводимости j = qnmE (где q – заряд электрона, n – концентрация электронов в единице объёма, µ – параметр, который связывает скорость с приложенным полем и является характеристикой рассеяния свободных носителей при дрейфовом пролёте в решётке, Е – сила поля).
В условиях безрассеянного (беспрепятственного) дрейфового пролёта электронов логично, что электрон в пролётном пространстве не генерирует (не продуцирует) процесс лавинизации электронной массы (классическое рассеяние электронов на фононах, электронах, примесных центрах и других), и, следовательно, такое понятие, как критическая напряжённость поля, теряет всякий смысл. То есть напряжённость поля в кристалле может быть сколь угодно большой, на порядки превосходя критическую напряжённость поля по зонной теории в полупроводниках, которая колеблется в пределах 105–2 × 106 В/см (в зависимости от ширины запрещённой зоны полупроводника и уровня легирующей примеси в переходных областях, в частности, в GaAs Ecrit = 2 × 105–4 × 105 В/см, в алмазе величина Ecrit – на порядок выше, чем в GaAs).
Безрассеянный пролёт электронов в мега-субтеравольтовых полях в кристаллической решётке GaAs c дипольной (ионной) поляризацией атомной структуры решётки будет в наномасштабе напоминать твёрдовакуумный ускоритель или тот же самый циклотрон (наноколлайдер), где скорость электрона будет определяться по «стандартной» релятивистской формуле:
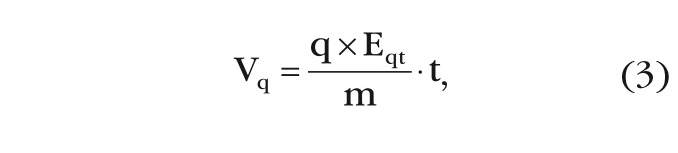
где q – заряд электрона, m – его циклотронная масса, t – время ускорения, а Eqt – внешнее электрическое поле, а точнее – разница между приложенным полем внешнего источника и полем внутренней поляризации ионно-связанного кристалла (Eqt = Евн – Eпол).
В классической физике принято, что начальная скорость электрона при нулевой напряжённости внешнего электрического поля равна нулю (v = µE). В данном случае следует предположить, что к моменту приложения поля к дрейфовому каналу электроны не обладают нулевой температурой по шкале Кельвина (kT = 0), то есть их скорость на длинах меньших, чем 4,5 нм в ионно-связанной решётке GaAs, в момент приложения электрического поля будет сходной с «ньютоновской», то есть:
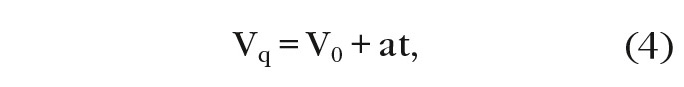
где
.jpg)
Из вышеприведённого следует, что электрон с циклотронной массой 9,11 × 10–28 г (1/1836 массы протона) и зарядом q = 1,60 × 10–19 к в сильных полях в дрейфовом канале с l ≤ 4,5 нм твердотельного вакуума в GaAs будет иметь все присущие релятивистскому кванту характеристики:
- энергию электрического поля (Wэ = qU/2 при U = 1,0 В) ≈ 0,8 × 10–19 Дж;
- энергию магнитного потока из условия ε0εE = µ0µE, то есть WM = 0,8 × 10–19 Дж;
- электромагнитную массу в твердотельном вакууме M = εε0µµ0W (кг);
- электромагнитный импульс p = (εε0µµ0)1/2 W (кг × м/с), магнитный момент MM = q/εεε0µµ02πV;
- спин О = qФ0π (Дж × с);
- волну де Бройля.
Возникает вопрос – можно ли разогнать электрон в баллистическом канале до уровня световой скорости в вакууме? Исходя из рассуждений, что:
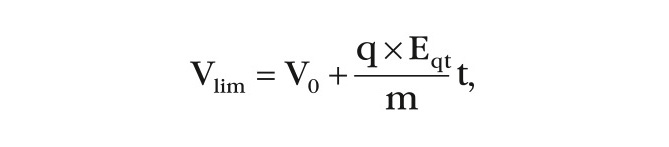
предельная скорость Vlim будет определяться не только начальной контактной скоростью, но и величиной напряжённости поля и временем пролёта. Хотя здесь мы можем столкнуться с логическим противоречием, что при L = 4,5 нм можно набрать гораздо большую энергию, чем на длине постоянной решётки GaAs L = a = 0,56 нм. На самом деле ожидается, что этого противоречия нет вследствие того, что будет возрастать роль эффекта сверхполевого туннелирования (свободное перемещение валентно-связанного электрона на внешней орбите атома в проводящее состояние). Другими словами, релятивистская валентная орбитальная энергия электрона переводится в энергию дрейфовой релятивистской проводимости со скоростью (V = V0 + аt). Неприкосновенность теории относительности Эйнштейна мы в данном случае не затрагиваем.
При безрассеянном дрейфе (пролёте) в сверхполях, допустим, при U = 10 В (то есть на два порядка выше классической критической напряжённости поля) мы предполагаем, что будут наблюдаться два явления проводимости в канале GaAs c L = 4,0 нм, как это было качественно показано в статье «Новая экстремальная электроника на основе LPE i-GaAs-монокристаллов» [4].
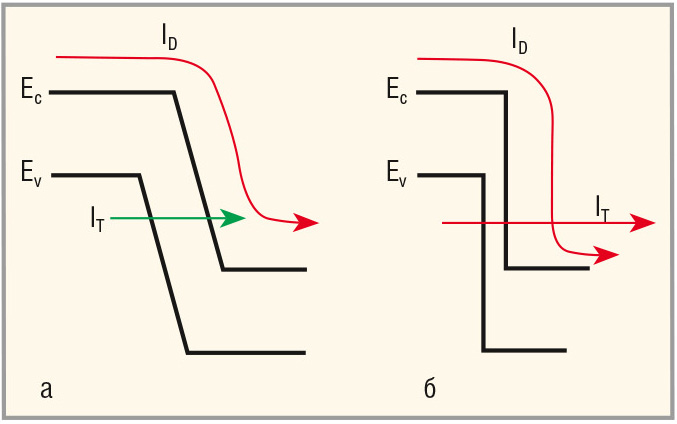
Из анализа диаграмм на рисунках 5а и 5б следует, что вероятность туннелирования электронов во втором случае гораздо выше, чем в первом, и она оценивается как:
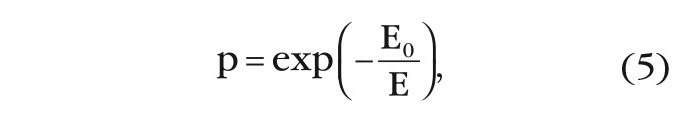
где:
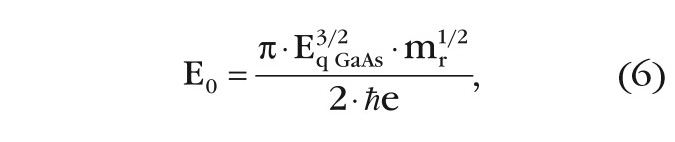
где:
EqGaAs = 1,43 эВ;
h – круговая постоянная Планка;
е – заряд электрона;
mr=mn×mp/mn×mp – приведённая эффективная масса электронов и дырок.
В случае, показанном на рисунке 5а, I = ID + IT, где IT << ID, то есть I = ID.
В случае, показанном на рисунке 5б, I = ID + IT, где IT » или > ID.
В итоге в первом случае (см. рис. 5а) ток обусловлен безрассеянным механизмом переноса, то есть идеальным проводником. Во втором случае (см. рис. 5б) – это классический пример сверхпроводника, то есть явления коллективного переноса электрического заряда.
Известно, что высокоэнергетичный электрон (допустим, бета-излучение изотопов, РЭМ – электроны, циклотронные пучки) обладает волной де Бройля λ = 1,22/E1/2, где [λ] = нм, а [E] = эВ, энергия электрона. При наличии потенциального барьера энергия электрона трансформируется в энергию гамма-рентгеновского излучения (X-rays). Следовательно, путём модуляции 2D-параметров сечения канала мы гипотетически можем набрать суммарную плотность потока электронов с огромными энергиями с последующим сверхплотным излучением гамма-квантов (гамма-лазер).
В вышеописанном случае приведён пример релятивистской проводимости, на базе которой можно реализовать исключительные энергетические возможности, абсолютно немыслимые на базе зонной проводимости. Например, сверхэффективный холодный катод (наноаналог РЭМ) или невероятно мощные лазеры с импульсным эквивалентом совокупности мощности Солнца (1023 Вт/см2) и другие. То есть это – гиперэнергия.
Приведём в кратком виде несколько моделей (из множества других вариантов) фотонной проводимости на основе взаимодействия фотонов (электромагнитных квантов) и зонных свойств ионно-связанного LPE i-GaAs-монокристалла.
Квантовый вентиль, или квантово-динамический варикап
В данном случае, при демонстрации модели квантово-динамического релятивистского вентиля (см. рис. 6) мы не демонстрируем «материнскую» модель квантового фото-FET вентиля, выполненного на основе глубокой физической и качественной переработки эффекта Франца–Келдыша, необходимого для СВЧ и терагерцового применения (усиление, генерация или функции волнореза (предохранителя) сверхмощных входных СВЧ ЭМИ) – это уже в прошлом. Здесь следует сосредоточить внимание на конструкции квантово-динамического вентиля, или, упрощённо, релятивистского варикапа.
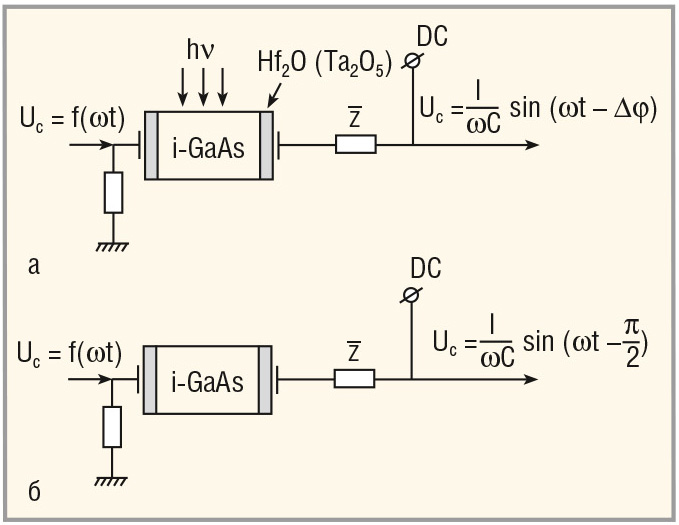
Сущность моделей заключается в модуляции зарядовой ёмкости системы на основе двух параметров из i-GaAs (e ≈ 12) и Hf2O (e ≈ 120). В случае (б) на рисунке 6 общая последовательная ёмкость очень незначительная, то есть Сб0 = Сi-GaAs.
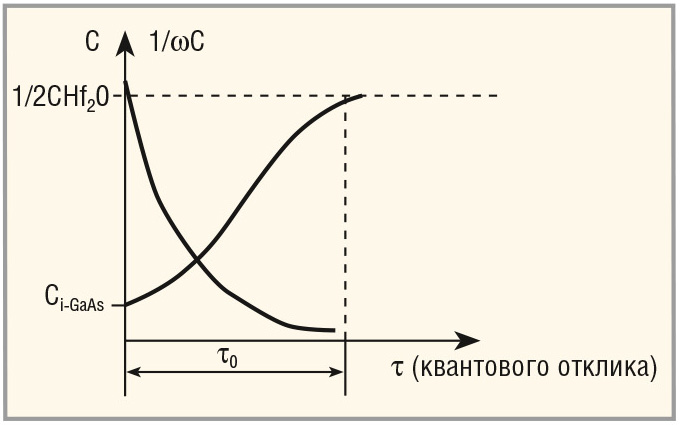
В случае (а) на рисунке 6 из-за резкого сброса квантовой ионизацией сопротивления изолятора i-GaAs с r > 109 Ом × см на десять порядков и более, что вытекает из взаимодействия энергетики LPE i-GaAs c внешними квантами hn и приложенного поля E (VDC) (см. диаграмму на рисунке 7). Тогда следует, что в случае (б) ёмкость системы i-GaAs/Hf2O на фиксированной частоте будет постоянной и равна Ci-GaAs. В случае (а) ёмкость сведётся к общей ёмкости ≈1/2, С СHf2O, при этом СHf2O >> Ci-GaAs.
Графически реактивный отклик квантово-релятивистского вентиля будет выглядеть так, как показано на рис. 7.
Приведённая конструкция фотонного вентиля (релятивистского варикапа), вероятно, будет пригодна для «фазо-укладки» в СВЧ-цепях АФАР, а также, в сочетании с нагрузкой Z, можно усиливать, делить, умножать и смешивать частоты.
«Диэлектрическая» релятивистская проводимость на основе монокристаллов LPE i-GaAs
Если LPE i-GaAS-диэлектрик поместить в постоянное внешнее поле, то физические процессы, связанные с механизмами поляризации, будут мало отличаться от аналогичных процессов в изоляторах, таких как Al2O3, SiO2, Si3N4, Ta2O5, Hf2O и других.
То есть при приложении статического поля токи утечки в i-GaAs-изоляторе будут иметь очень низкие, микроскопические значения, что показано на рисунке 8.
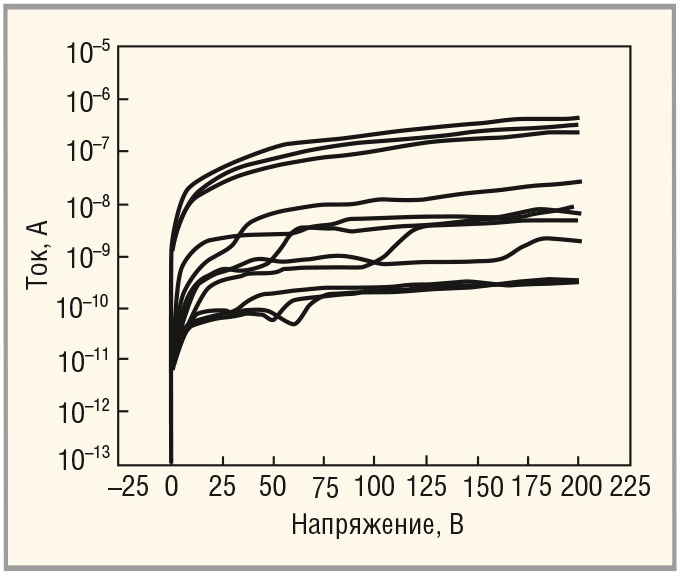
В данном конкретном случае приводится демонстрация токов утечки в i-GaAs-слое p–i–n GaAs-структуры с ALD пассивацией поверхности i-GaAs-структур ALD-изолятором Al2O3 толщиной » 15 нм, полученной в Мордовском государственном университете им. Н.П. Огарёва, г. Саранск (д.т.н. К.Н. Нищев). Для информации: замеры произведены в Институте физики в Эстонии, г. Тарту.
Несмотря на приличную наноамперную составляющую обратного тока p–i–n GaAs-конденсатора, которая обусловлена, в основном, не самой пока лучшей или отработанной ALD-технологией пассивации на установках фирмы Beneq (Финляндия), тем не менее, можно говорить о свойствах готового к применению i-GaAs-изолятора. Повышение рабочей температуры i-GaAs-кристалла не приводило к катастрофическому росту тока и, в целом, был достигнут блестящий обнадёживающий результат: ток утечки p–i–n GaAs-конденсатора составил при температуре кристалла Tj = 300°C не более 10–6 А/мм2, что при параметре удельной ёмкости в 1,5–1,8 пФ/мм2 вполне допустимо для построения сверхдобротных (до 10 000) СВЧ-GaAs варикапов, как полевых, так и релятивистских.
При приложении переменного электрического поля к ионно-связанному LPE i-GaAs-диэлектрику с увеличением частоты СВЧ-сигнала w поляризуемость ионно-связанной молекулы GaAs будет постепенно запаздывать относительно частоты сигнала, что приведёт к изменению диэлектрической проницаемости (или к дисперсии e).
На рисунке 9 приведена классическая зависимость диэлектрической проницаемости от частоты проходящего через тело диэлектрика высокочастотного сигнала [11].
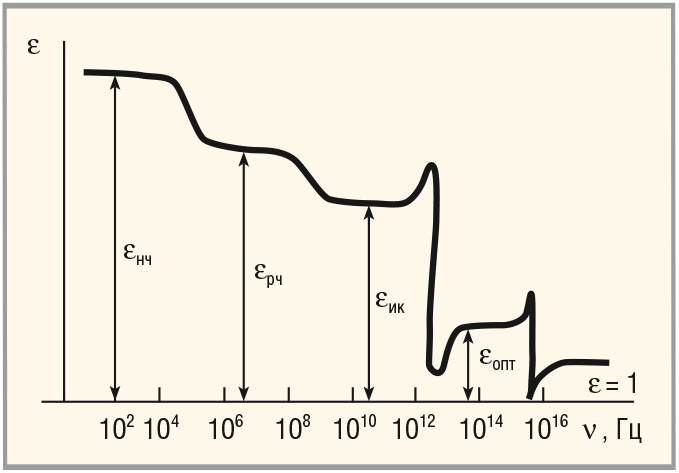
В работе Павлова и Хохлова [11] показано, что на частотах 104–105 Гц гасятся разновидности объёмно-зарядовой поляризации (электроны, ионы). При повышении частоты волны, проходящей через диэлектрик, до 105–1011 Гц диэлектрическая проницаемость уменьшается вследствие ослабления тепловых механизмов поляризации (электронная, ионная, дипольная). «При частотах, соответствующих инфракрасной области спектра (1012–1015 Гц) происходит запаздывание ионной упругой и дипольной упругой поляризации. В области оптических частот (1015 → 1017 Гц) диэлектрическая проницаемость обусловлена только электронной упругой поляризуемостью. В полях с частотами выше 1017–1018 Гц поляризация уже невозможна и ε = 1» [11].
Далее, исходя из уравнений Максвелла, показатель преломления
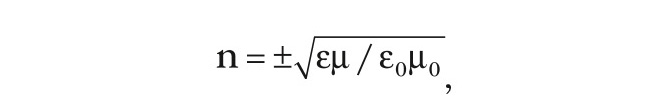
где µ – относительная магнитная проницаемость диэлектрика. Тогда, с учётом того, что на оптических частотах µ ≈ 1, следует, что εopt = n2.
Необходимо отметить, что электронная упругая поляризуемость в LPE i-GaAs ожидается значительно ранее, то есть в более ближнем частотном диапазоне, точнее, в среднем инфракрасном диапазоне длин волн.
Вышеперечисленные законы поведения ε = f(ω) позволяют реализовать совершенно новые конструкции LPE i-GaAs-приборов на основе уже не зонной, а фотонной проводимости.
Приведём простейший пример такой конструкции триодного типа.
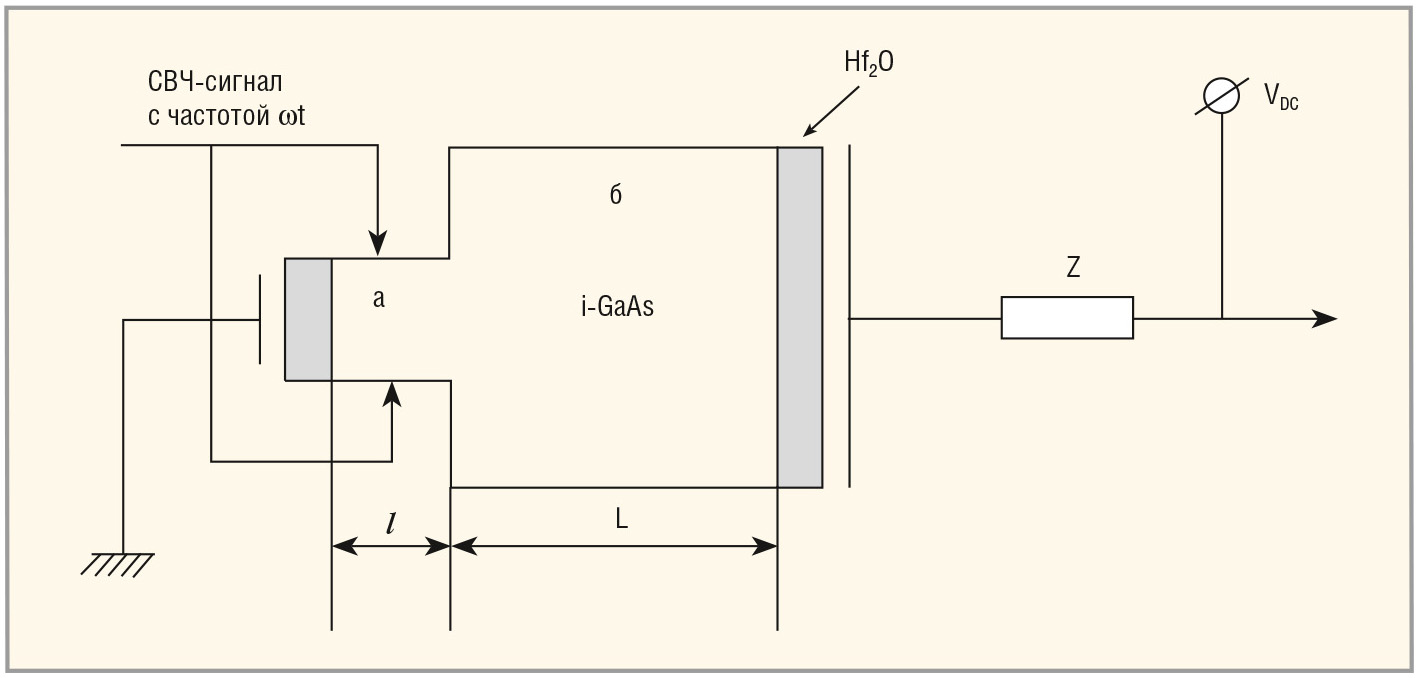
Структуру изолятора, показанную на рисунке 10, можно представить в виде комбинации ёмкостей (конденсаторов) на основе Hf2O (ε > 120) и i-GaAs (e ≈ 12). Общая ёмкость такой последовательной комбинации ёмкостей будет обусловлена в основном ёмкостями областей (а) и (б) i-GaAs-структуры. Предположим, что l + L » 50 мкм, тогда напряжение пробоя такой структуры составит не менее 1200 В. Электромагнитная волна пройдёт это расстояние за:
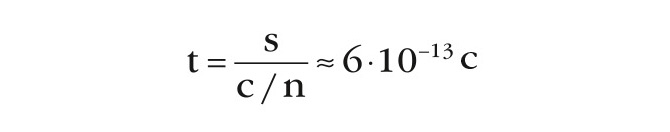
(или ω ≈ →300 ГГц).
Другими словами, при VDC = 1000 В можно оперировать частотами в субтерагерцовом диапазоне 100–500 ГГц (!) при очень приличных уровнях мощ-ности.
Для справки: GaAs MHEMT D0071H ф. OMMIC (Франция) с предельной частотой в 300 ГГц (длина канала 70 нм) функционируют при предельном напряжении питания VDC ≤ 3,0В.
При приложении СВЧ-сигнала к (а)-области i-GaAs структуры диэлектрическая проницаемость (а)-области изменится в сторону уменьшения, что вызовет в целом изменение реактивного сопротивления при фиксированном значении VDC в цепи системы i-GaAs/Hf2O, как это показано в общем виде на рисунке 11.
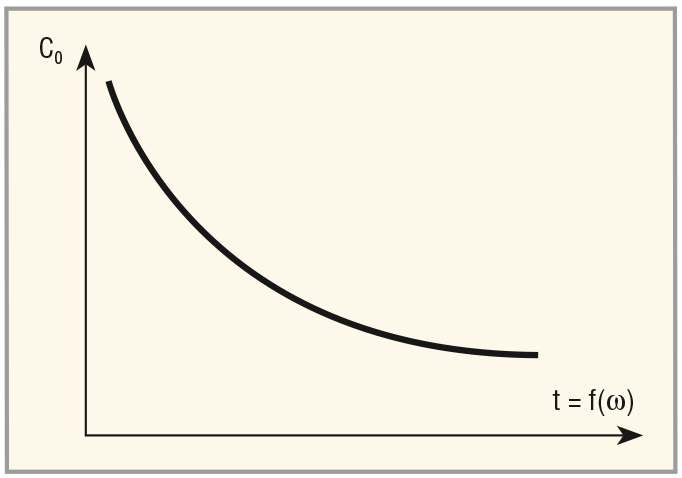
Следовательно, мы будем иметь эффект динамической электромагнитной генерации в системе i-GaAs/Hf2O, который будет пропорционален изменению ε(а)i-GaAs и далее e(б) i-GaAs, и, соответственно, общей релятивистской составляющей 1/ωобщ. i-GaAs. Меняя частоты, мы будем иметь разные импедансы Z системы i-GaAs/Hf2O:
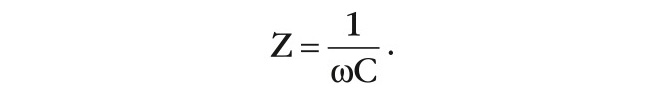
Расчётные параметры триодного терагерцового генератора показаны на рисунке 12.
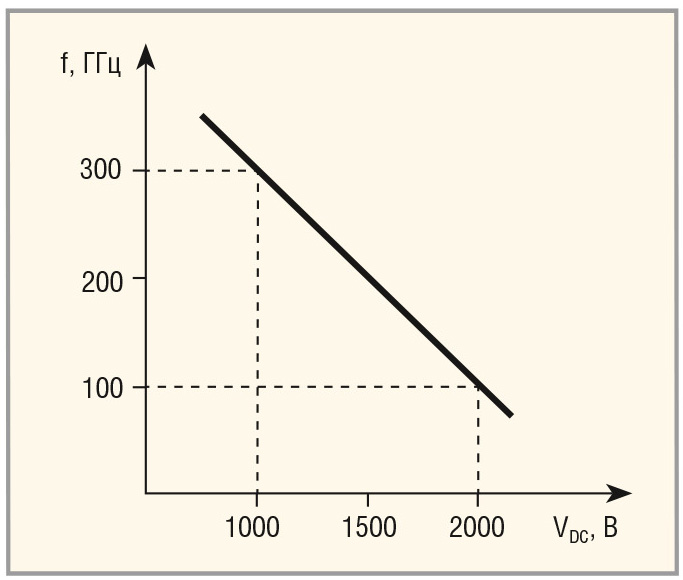
Таким образом, получается, что на базе приведённой триодной структуры можно построить:
- генератор СВЧ-частот;
- усилитель;
- смеситель;
- умножитель;
- фазовращатель.
При этом необходимо учесть, что данный триод не имеет статических потерь, связанных с потерями постоянной остаточной мощности в типичных транзисторах или диодах, которая усиливается с ростом частоты сигнала. Очевидно, что и коэффициент шума на СВЧ-частотах в таком релятивистском генераторе будет на сверхмалом уровне.
Оптический модулятор для ВОЛС цифроаналогового СВЧ-применения
Как известно, скорость светового кванта в прозрачной среде определяется по формуле:
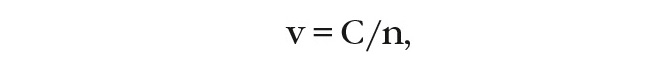
где n – показатель оптического преломления среды, C – скорость электромагнитной волны фотона в вакууме.
Показатель преломления зависит от электромагнитных свойств среды, а точнее, от диэлектрической и магнитной проницаемостей. Закон изменения коэффициента преломления n определяется формулой, с помощью которой советский физик В.Г. Веселаго показал теоретическую возможность отрицательного коэффициента преломления:
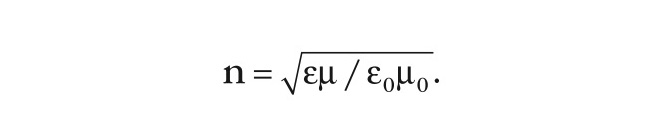
На практике при рассмотрении анизотропии прохождения световой волны в кристалле, например, при расчёте показателей коэффициента преломления по кристаллографическим осям, используют упрощённое значение формулы показателя преломления:
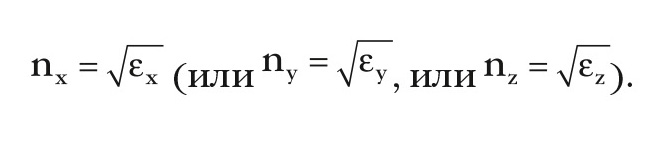
С учётом зависимости диэлектрической проницаемости e от частоты волны в изоляторе, показанной на рисунке 9, совершенно очевидно, что можно манипулировать световой волной с созданием эффективного i-GaAs-модулятора Маха-Цандера, показанного на рисунке 13.
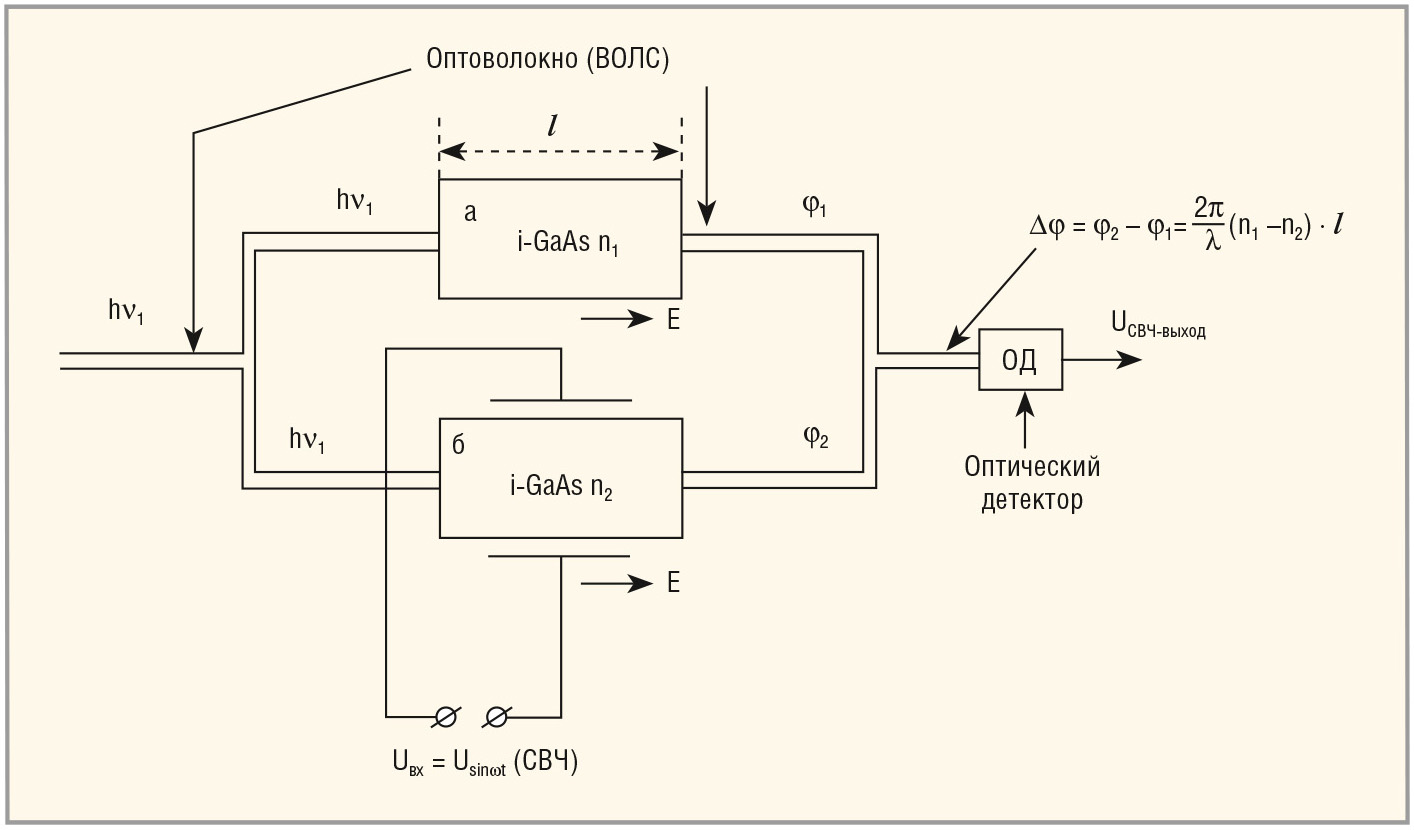
Конструкция оптического модулятора Маха-Цандера работает следующим образом:
- световая волна в канале (а) движется со скоростью v1 = C/n1, где n1 – показатель преломления GaAs;
- в канале (б) световая волна движется ускоренно из-за эффекта n≈√ε, то есть v2 = C/n2;
- разница фазовых скоростей световой волны Δφ = φ2 – φ1 считывается и демодулируется фотодетектором, который воспроизводит колебания входного СВЧ-сигнала Uвх. = Usinωt.
Показанный модулятор Маха-Цандера на основе LPE i-GaAs-монокристалла гораздо эффективнее зарубежных аналогов на основе MOCVD i-GaAs-полуизолятора, что связано с резко отличающейся дефектностью эпитаксиальных слоёв GaAs (MOCVD и LPE) в пользу исключительно качественных LPE-слоёв i-GaAs. Описанная модель физически качественно новая, более ёмкая и гораздо более эффективная по сравнению с линейным электрооптическим эффектом Поккельса.
Заключение о перспективности LPE i-GaAs-электроники и фотоники
В настоящей статье, как и в предыдущих публикациях, показана физическая интерпретация сверхэнергетических возможностей релятивистской наноэлектроники, высокая вероятность реализации электронной и фотонной «комнатной» сверхпроводимости и влияние вышеуказанных сверхтехнологий на геополитический ландшафт планеты.
В статье раскрываются новые возможности LPE i-GaAs-электроники и фотоники на платформе новых физических открытий, явлений, физических моделей и конструкций, таких как COOL-инжекция [12], одновременная биполярная модуляция собственного электрохимического потенциала EF, модуляция типа проводимости концентрацией одной и той же амфотерной примеси, усовершенствованный эффект Франца–Келдыша, абсолютно новый эффект квантового вентиля, новый эффект СВЧ и терагерцовой «диэлектрической» фотонной проводимости, новый эффект оптической модуляции взамен линейного электрооптического эффекта Поккельса и других. Можно долго перечислять абсолютно новые физические модели конструкций силовых и СВЧ-приборов, например, интегрального MOS-SIT-FET или чисто электронного GaAs – аналога биполярных кремниевых IGBT с частотами на два порядка выше, или «беспяточного» (прямая ВАХ) GaAs высоковольтного диода и так далее.
Подчеркнём также, что из данной статьи исключён раздел «Оптические DRAM», что, вероятно, будет являться предметом очередной публикации.
Коммерциализация Flash-NAND, 3D-XPoint энергонезависимой памяти фактически грозит превратить современные цифровые системы в крупногабаритные арифмометры. В связи с этим исследования по созданию i-GaAs фотонной памяти, а также i-GaAs JHMOS-Flash SRAM с пета-циклом перезаписи и, комплектно, JHMOSFET DRAM (по единой, универсальной технологии) приобретают большую ценность для отечественной цифровой спец-техники.
Кристаллографическое совершенство LPE i-GaAs-кристаллов (на 2–3 по-рядка более низкая дефектность по сравнению с западными MOCVD/MLE i-GaAs-полуизоляторами) позволяет создавать как высокотемпературные радиационно-стойкие системы на кристалле (AlGaAs/GaAs, ZnSe/GaAs c Tj = 350–400°C), так и системы на кристалле субтерагерцового диапазона (100–800 ГГц) на основе GaAs/Ge с активными областями до 1,0 см2 (ТКР и постоянные решёток Ge и GaAs – идеально идентичны, но при этом подвижность дырок в Ge очень высока, точнее, гораздо выше подвижности электронов в GaN; подвижность электронов в Ge и GaAs по сравнению с GaN выше в 3,5 раза и в 7 раз соответственно).
Приведённые в данной публикации идеи и модели находятся на стадии патентования.3
Литература
- www.so-l.ru/news/show/ibm_predstavila_processor_budushego_s_7_nanometro.
- Гордеев А.И. Электроника как одна из основ национального суверенитета. Силовая электроника. 2014. №6.
- Vainshtein S.N., Yuferev V.S., Kostamovaara J.T., Kulagina M.M., Moilanen H.T. Significant Effect of Emitter Area on the Efficiency, Stability and Reliability of Picosecond Switching in a GaAs Bipolar Transistor Structure. Transactions on Electron Devices. 2010. Vol. 57. №4.
- Войтович В.Е., Гордеев А.И., Думаневич А.Н. Новая экстремальная электроника на основе LPE i-GaAs-монокристаллов. Современная электроника. 2014. №6.
- Физические величины. Справочник под ред. Григорьева И.С. Мейлихова Е.З. М. Энергоатомиздат. 1991.
- Алёшкин В.Я. Курс лекций «Современная физика полупроводников». Н. Новгород. 2013.
- Зи С.М. Физика полупроводниковых приборов. Пер. с англ. под ред. Трутко А.Ф. М. Энергия. 1973.
- Ashkinazi German et al. Process for Fabricating Intrinsic Layer and Applications. US Patent 5,733,815. 1998. 31 Mar.
- Ашкинази Г.А. и др. Описание изобретения к авторскому свидетельству SU 1072686.
- Андреев В.М., Долгинов Л.М., Третьяков Д.Н., ред. Алфёров Ж.И. Жидкостная эпитаксия в технологии полупроводниковых приборов. М. Сов. радио. 1975.
- Павлов П.В., Хохлов А.Ф. Физика твёрдого тела. М. Высшая школа. 2000.
- Войтович В.Е., Гордеев А.И., Думаневич А.Н. Новые возможности GaAs силовой электроники. Силовая электроника. 2014. №2.
Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!