Мостовые схемы как основа измерительных модулей Dataforth

Сэмюэл Хантер Кристи (1784–1865) родился в Лондоне в семье Джеймса Кристи, основателя аукционов изобразительного искусства Christie’s Fine Art Auctioneers. Сэмюэл изучал математику в Тринити-колледже и после его окончания почти 50 лет преподавал в Королевской военной академии. Кристи внёс большой вклад в развитие учений о магнетизме, например, в изучение зависимости магнитных сил от температуры и воздействия солнечных лучей на земной магнетизм. В 1833 году он опубликовал статью о магнитоэлектрической проводимости различных металлов, показав, как проводимость провода изменяется обратно пропорционально длине и прямо пропорционально квадрату диаметра провода. К сожалению, работы Кристи стали известны лишь после публикаций Уитстона. Хотя Чарльз Уитстон (английский физик и изобретатель) и признал ценность работ Кристи; он был первым, кто широко использовал схему, носящую его имя, и разработал для неё множество важных приложений. По сей день (162 года спустя) мост Уитстона остаётся наиболее чувствительным и точным методом измерения значений сопротивления. Сэмюэл Кристи так и не получил признания за свою схему с мостом. Представьте себе, какой доход принесла бы сегодня оригинальная схема, изобретённая Кристи, при гонораре всего в пять центов за каждую использованную мостовую схему.

Как уже было сказано выше, мостовые схемы используются уже более 150 лет. На сегодняшний день мост по-прежнему является наиболее экономичной схемой для точного измерения различных видов электрических величин, в том числе и сопротивления. Первоначальная топология мостовой схемы претерпела множество модификаций и применялась в таких приложениях, как измерение переменного тока, автоматическая балансировка, в различных генераторах и усилителях. Возможно, наиболее известным применением схемы Сэмюэля Хантера Кристи является мостовое включение тензорезисторов для измерения типа деформации в механических узлах и строительных конструкциях. Как один из мировых лидеров в области разработки и производства модулей согласования и нормализации сигналов, компания Dataforth с успехом использует мостовые схемы в своих разработках.
А технические специалисты компании поделились основными принципами работы, но больше внимания уделили тонкостям возбуждения мостовой схемы и связанным с ней характеристикам.

Базовые мостовые схемы

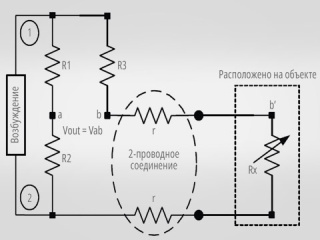
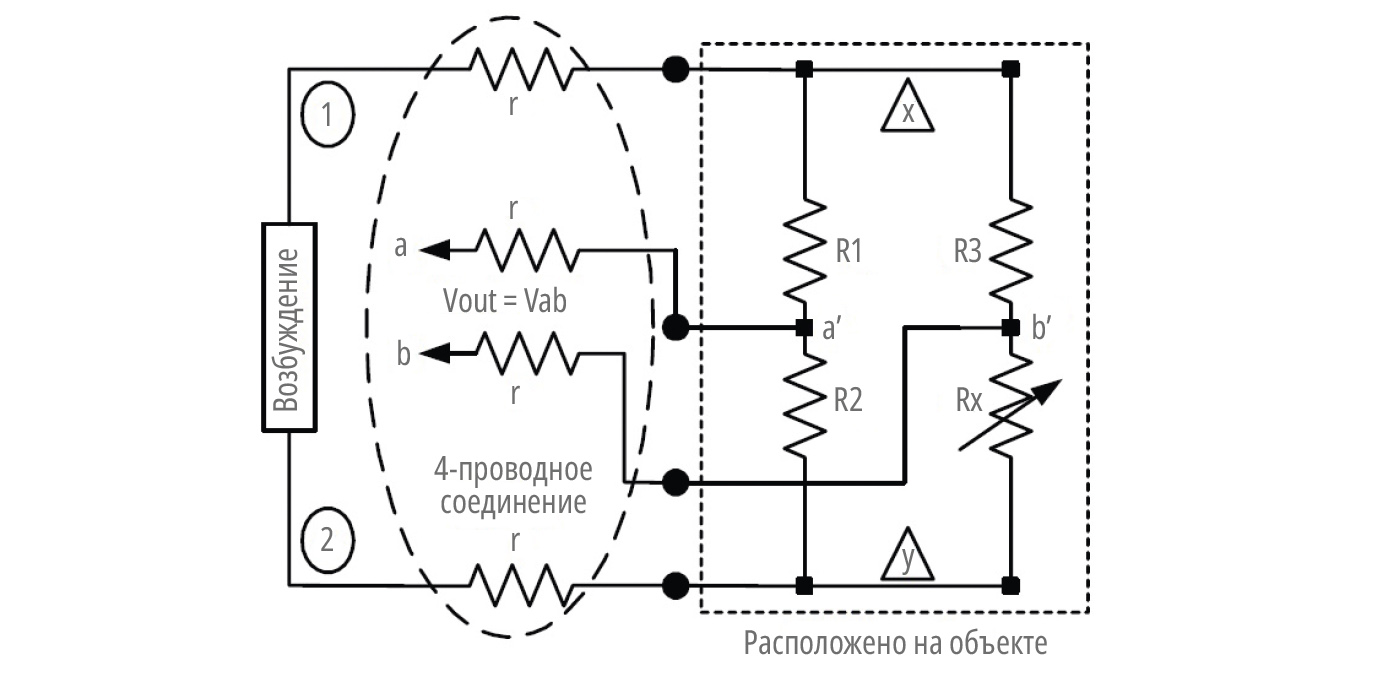
В приведённых ниже примерах основное внимание уделяется топологиям мостовой схемы, показанной на рис. 1, с одним резистивным переменным элементом. Исследуются выходные характеристики, в том числе влияние сопротивления цепи на мостовое возбуждение как по напряжению, так и по току, а также линейность моста. Погрешностями из-за сопротивлений плохо выполненных контактов и коррозии из-за контакта разнородных металлов пренебрегают. Более того, сопротивлением выходной линии также пренебрегают, поскольку стандартной практикой является измерение выходного напряжения моста устройствами с высоким импедансом (обычно > 1 МОм).

Аналитические исследования в этом документе сосредоточены на мостовом сопротивлении, что означает, что все резисторы моста имеют сопротивление «R», когда они не подвергаются воздействию переменных процесса возбуждения. На рис. 1 показан датчик поля R-омного мостового типа со всеми мостовыми резисторами (R₁, R₂, R₃, R_x), расположенными в точке измерения поля; однако, поскольку резистор R_x является резистивным сенсорным элементом моста, его сопротивление изменяется в зависимости от параметров контролируемого процесса, таких как температура, расход, давление, уровень, влажность, деформация и т.д. Во всех топологиях резистивного моста R₁, R₂, R₃ равны R, а R_x = (R+ΔR), где ΔR – функция переменных процесса.

Примеры

В дальнейшем будут рассмотрены топологии двух категорий резистивного моста. Резистивные мосты, относящиеся к категории 1, определяются как топология, в которой все резисторы расположены на объекте, а один или несколько элементов подвергаются воздействию переменной процесса. Мосты категории 2 определяются как имеющие один или несколько резистивных сенсорных элементов моста, расположенных на объекте и подверженных воздействию переменных процесса, и остальных резисторов, расположенных в точке электрического возбуждения. Мосты с одним или двумя элементами переменной процесса часто называют четверть- и полумостами соответственно.

Мост категории 1 с возбуждением по напряжению

Этот пример иллюстрируется рис. 1, где источником возбуждения является напряжение V12. Фактическое напряже­ние возбуждения моста V_xy непостоян­но из-за падения напряжения на сопро­тивлении цепи возбуждения. Выходное напряжение моста V_out = (V_a – V_b) = V_ab. Если V_ab всегда измеряется с помощью вольтметра с высоким импедансом (обычно > 1 МОм), то сопротивлением измерительной линии можно прене­бречь, и V_ab = V_a´b´. 

В качестве примера влияния сопротивлений измерительных линий предположим сопротивление линии 10 Ом, вольтметр с входным сопротивлением 1 МОм и мост 120 Ом. Ошибка, вноси­мая вольтмет­ром на клеммы a´–b´, составляет приблизительно 0,99988, тогда как на клеммы a–b она составляет приблизительно 0,99987, или разница составляет –0,001%.

Уравнение 1 иллюстрирует выходное напряжение V_out = V_ab на рис. 1 без учёта всех сопротивлений цепи.

Уравнение 1 является классическим уравнением баланса моста, определяющим набор номиналов резисторов, уравновешивающих мост, в результате чего выходное напряжение моста равно нулю, V_ab = 0. Это условие возникает, когда R₁×R_x = R₂×R₃. Также стоит отметить, что классическое условие баланса моста действует независимо от сопротивления цепи и значения напряжения возбуждения.

В статье Кристи (1833 г.) показано, что если R_x неизвестно, а R₂ = R₁, то выходное напряжение моста будет равно нулю, когда R₃ настроено равным переменному сопротивлению R_x. Во многих промышленных преобразователях используются мостовые схемы с одним или несколькими мостовыми сопротивлениями, которые зависят от переменных процесса, таких как температура, давление, деформация, влажность и т.д. В этих ситуациях преобразователи на основе мостовой топологии не могут быть идеально сбалансированы в полевых условиях; поэтому измеряются ненулевые выходные мостовые напряжения. В отличие от балансных измерений, возбуждение моста и сопротивление цепи будут вносить свой вклад в ошибки измерения.

Промышленные преобразователи с топологией мостовой схемы имеют наборы резисторов, которые уравновешивают мост в каком-то состоянии, определяемом конкретным входным параметрическим полем. Когда эти параметры устойчивого состояния изменяются, мост становится несбалансированным, и выходной сигнал становится ненулевым. 

Измерение этого напряжения разбаланса с применением соответствующего коэффициента является косвенным измерением переменной поля. Полезный диапазон этих напряжений определяется в промежутке от микровольт до милливольт; следовательно, необходимо использовать методы измерения низкого напряжения.

Уравнение 2 представляет собой выходное напряжение топологии мостовой схемы R-ом, показанной на рис. 1, с возбуждением по напряжению, вклю­чая сопротивление цепи возбуждения.

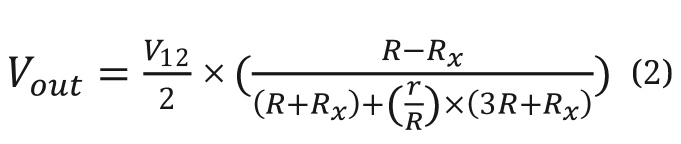
Если пренебречь сопротивлением цепи возбуждения, это уравнение сво­дится к:

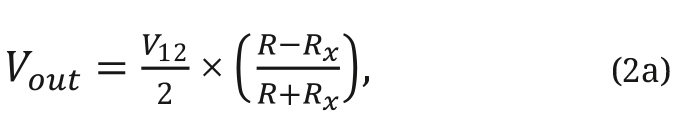
где сопротивление цепи r = 0.

На рис. 2 представлен график выходных характеристик моста с типовым значением 120 Ом, схема которого была показана на рис. 1 (с переменным сопротивлением R_x). В этой модели возбуждение составляет 5 В постоянного тока, R_x находится в диапазоне от 20 Ом до 220 Ом, и используются три различных сопротивления линии возбуждения – ноль, 5 Ом и 20 Ом (нижняя кривая 1: сопротивление линии 0 Ω; средняя кри­вая 2: сопротивление линии 5 Ω; верхняя кривая 3: сопротивление линии 10 Ω). Сопротивлением выходной линии пренебрегают.

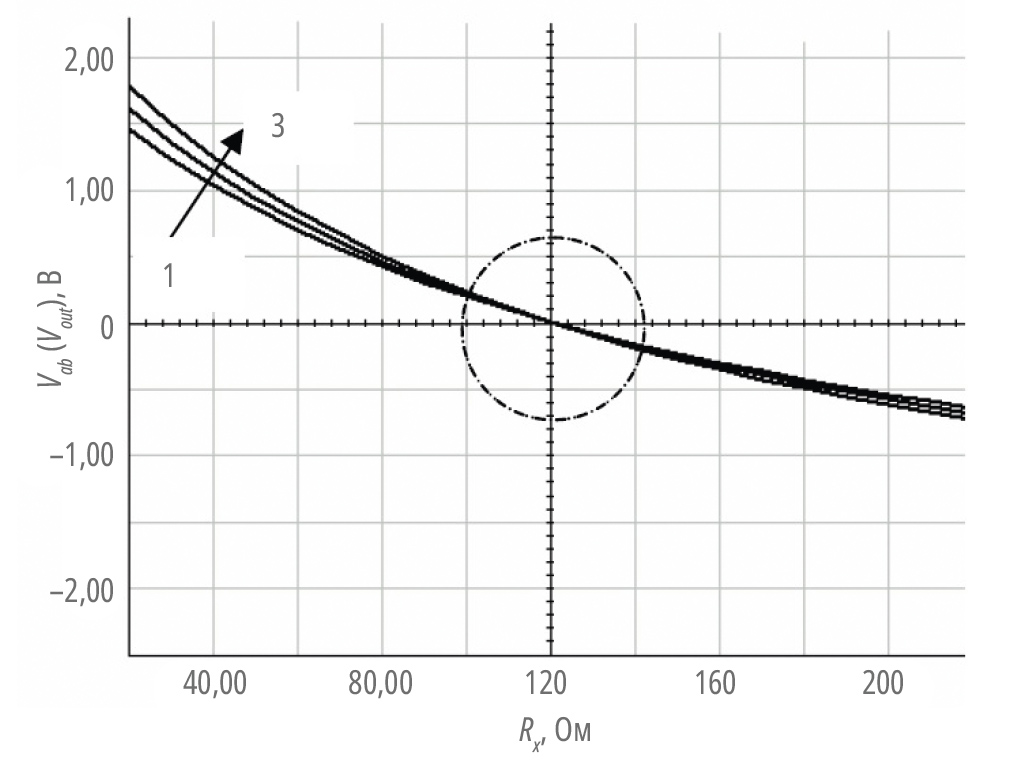
На основании данного графика и уравнения 2 можно сделать некоторые важные выводы о мостах, относящихся к категории 1:

1. выходные характеристики схемы чувствительны к сопротивлению линии возбуждения, а также к напряжению возбуждения – V₁₂;
2. выходное напряжение моста является нелинейным для номинальных изменений Rx независимо от сопротивления линии возбуждения и напряжения возбуждения;
3. по мере уменьшения диапазона изменения R_x выходное напряжение моста начинает приближаться к нулю и становится более линейным. 

На рис. 2а показано, что выходное напряжение моста по-прежнему остаётся линейным при очень небольших изменениях R_x и чувствительным к сопротивлению линии возбуждения.

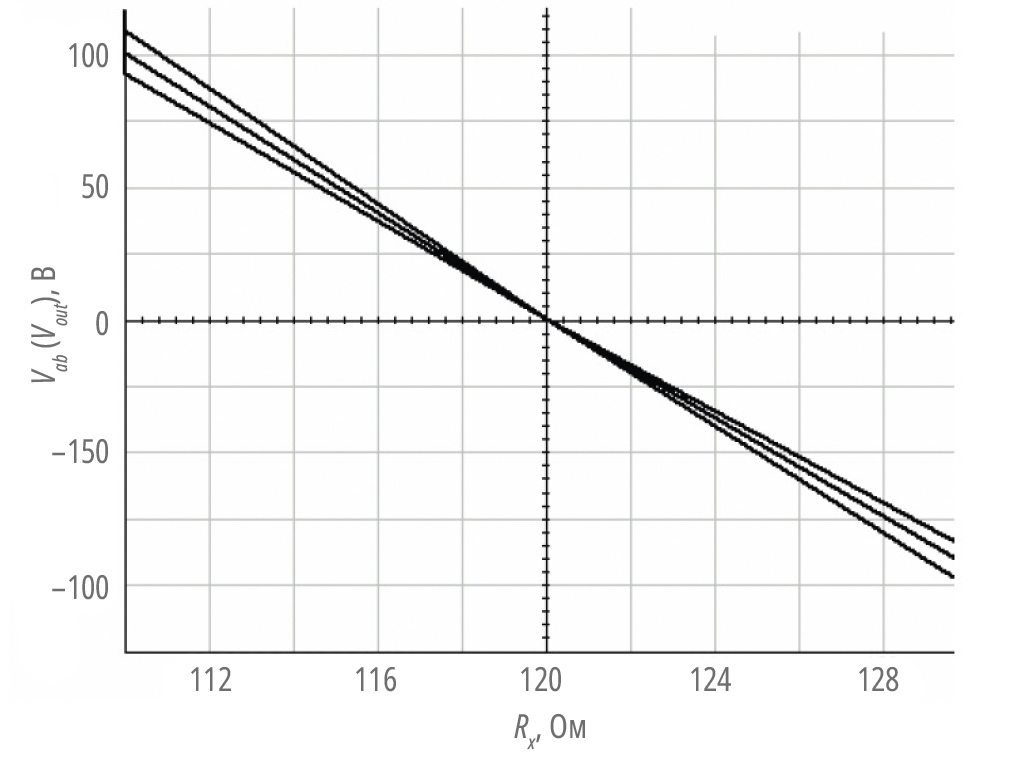
Но может ли выходное напряжение мостовой схемы, показанной на рис. 1, стать линейным? Чтобы ответить на этот вопрос, уравнение 3 представляет собой частную производную выходного напряжения резистивного моста V_out в уравнении 2a по отношению к R_x (изменение V_out  при изменении R_x), при этом все остальные переменные считаются постоянными и сопротивление линии возбуждения отсутствует.

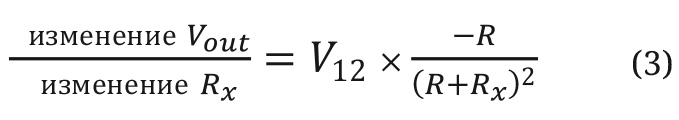
Ясно, что уравнение 3 является нелинейной функцией и непостоянной, что является условием, необходимым для того, чтобы Vout был линейной функцией от R_x. Таким образом, мостовые схемы, показанные на рис. 1, не могут иметь выходной сигнал, линейно зависящий от R_x (см. рис. 3).

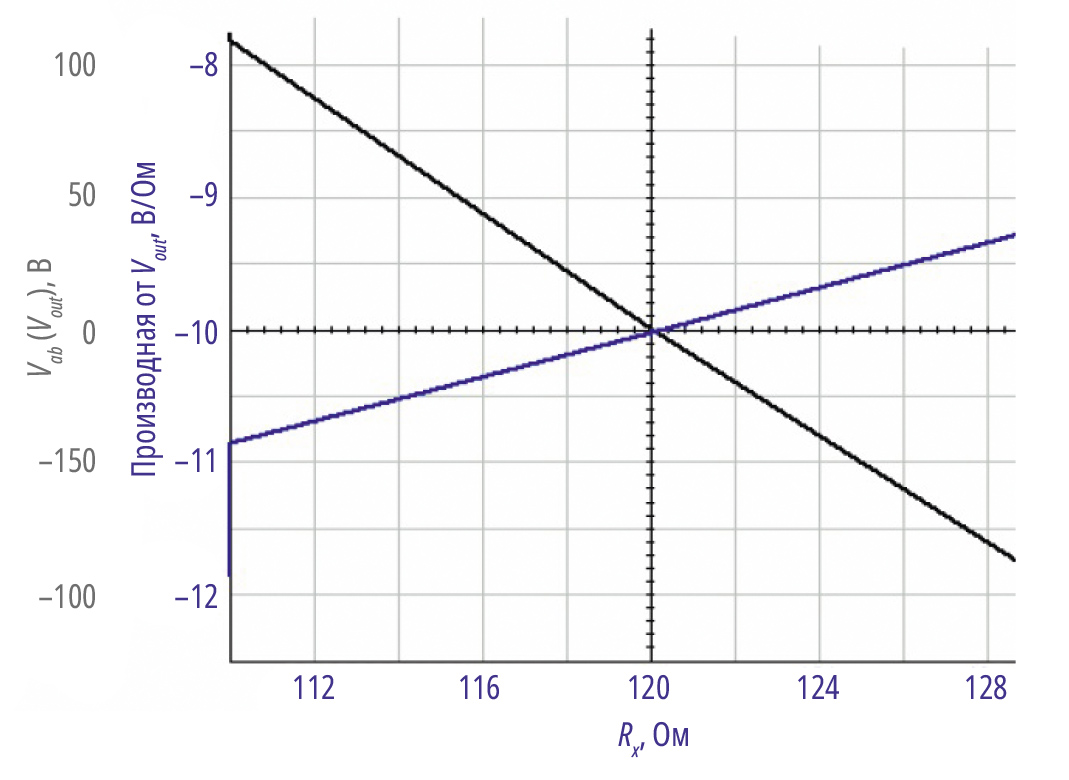
Для R_x в диапазоне от 110 до 130 Ом изменения V_out с изменениями R_x (урав­нение 3 и рис. 3) находятся в диапазоне от –11,3 до –9,6 мВ на Ом при среднем значении –10,5 мВ.

Однако использовать частные производные при расчёте выходных сигналов моста нецелесообразно. Общепринятой практикой является признание того, что мостовые схемы имеют нелинейные выходы, на которые влияет сопротивление линии возбуждения, и использование данных передаточной функции и инструкций по установке мостовых датчиков, указываемых непосредственно производителями.

Резистивный мост с токовым возбуждением

Уже более века используются мостовые схемы с возбуждением напряжением. На сегодняшний день, благода­ря современным полупроводниковым технологиям, возможно также возбуждение от источника тока. 

Уравнение 4 описывает выходной сигнал токового возбуждённого резистивного моста с пренебрежением сопротивлением линии выходного напряжения и при отсутствии сопротивления линии возбуждения.

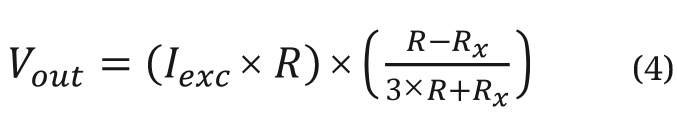
Уравнение 4 становится уравнением 4a, когда ток возбуждения устанавливается равным I_exc = (V₁₂ / R).

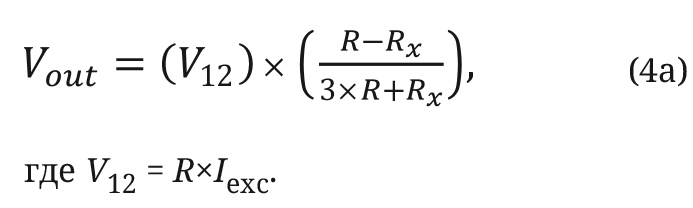
где V₁₂ = R×I_exc.

Здесь следует обратить внимание на сходство уравнений 2a и 4a.

Уравнение 5 представляет собой частную производную резистивного моста Vout в уравнении 4a по отношению к Rx (изменение Vout при изменении Rx), при этом все остальные переменные считаются постоянными.

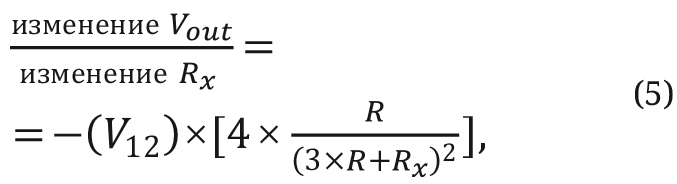
где V₁₂ = R×I_exc.

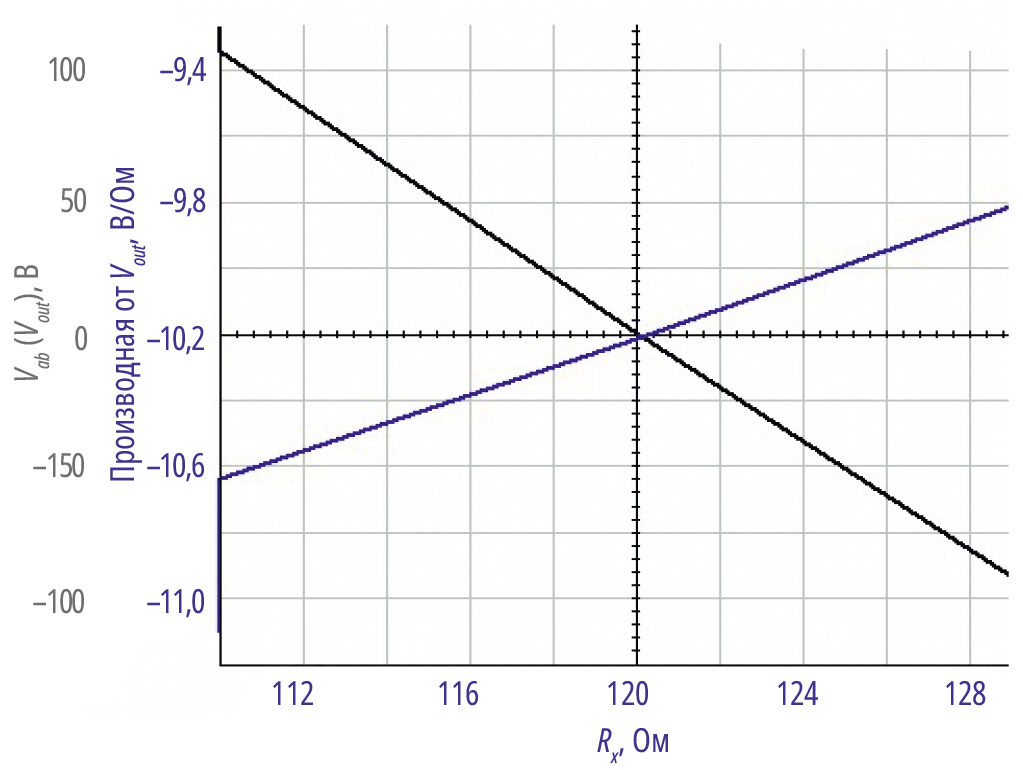
На рис. 4 и 5 показано визуальное сравнение выходных напряжений резистивного моста категории 1 при возбуждении как по напряжению, так и по току.


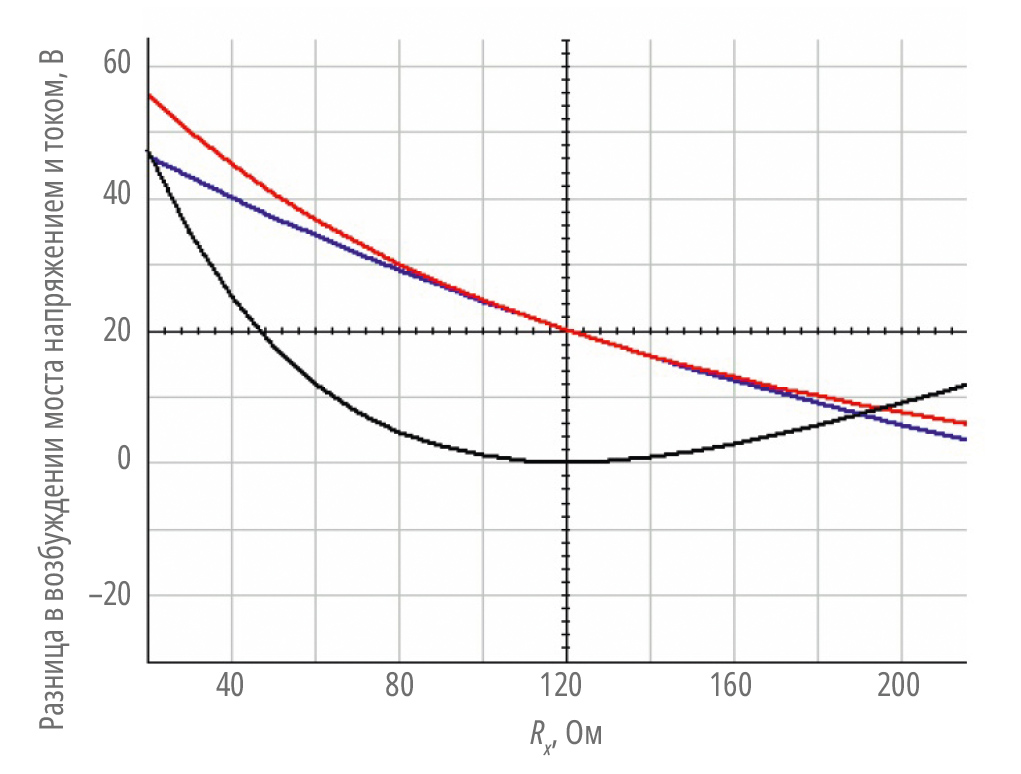
На рис. 4 показаны характеристики мостовой схемы с сопротивлением 120 Ом, с возбуждением от источника тока на клеммах 1 и 2, где сопротивление линии равно нулю. Значение этого источника тока было выбрано равным 41,667 мА, что составляет 5 В постоянного тока / 120 Ом. Это значение тока обеспечивает возбуждение 5 В постоянного тока на клеммах моста, когда сопротивление R_x равно 120 Ом, что соответствует состоянию отсутствия параметрических входов поля.

На рис. 5 показано, что поведение выходного сигнала для моста сопротивлением 120 Ом, с током возбуждения, включающим различные сопротивления линии, равные нулю, 5 и 10 Ом, не зависит от сопротивлений линии возбуждения. При этом изменение Vвых при изменении Rx варьируется от –10 до –10,8 мВ/Ом при среднем значении –10,4 мВ/Ом, примерно такое же, как и при возбуждении напряжением, но явно всё же не постоянное.

Сравнение возбуждений резистивного моста категории 1

Выводы, приведённые ниже, основаны на схеме моста сопротивлением 120 Ом, показанной на рис. 1, с возбуждением напряжением 5 В постоянного тока или возбуждением током 41,67 мА, с включёнными сопротивлениями линии возбуждения 0, 5 и 10 Ом и пренебрежением сопротивлением линии выходного напряжения.

1. Уравнения 4, 4a и рис. 5 (чёрная кривая) показывают, что для токового возбуждения выход резистивного моста, не зависит от сопротивления линии возбуждения.
2. На рис. 4 показано, что если пренебречь сопротивлением линии, то выходной сигнал 4-проводного моста более линейный в широком диапазоне R_x для возбуждения по току (синяя кривая), чем для возбуждения по напряжению (красная кривая).
3. Уравнение 6 и рис. 4 (чёрная кривая) показывают, что выходные сигналы моста, проиллюстрированные возбуждением по напряжению (уравнение 2a) и возбуждением по току (уравнение 4a), по существу идентичны вблизи баланса. Вблизи баланса можно предположить, что R >> ΔR. Обратите внимание, что R_x = (R + ΔR), а Iexc определяется как V₁₂ / R.

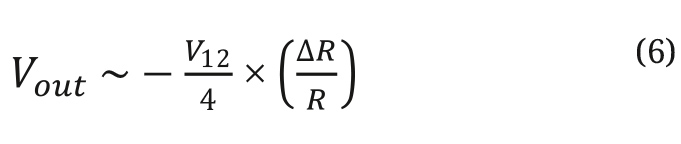
В типовых решениях тензодатчиков, где изменения R₁, R_x равны положительному значению, а изменения R₂, R₃ равны отрицательному значению, уравнение 6 принимает вид:

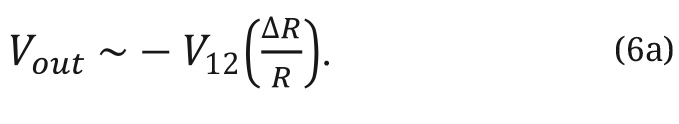
Выбор схемы возбуждения

Сопротивления линий возбуждения по-разному влияют на выходные напряжения моста в зависимости от категории, к которой он относится (категория 1 или 2), и используемого источника возбуждения (ток или напряжение). На рис. 6 и 7 показано выходное поведение резистивных мостов категории 2 с одним резистором, расположенным в поле, подключённым к остальной части моста двумя и тремя проводами соответственно. Ниже приведены выражения выходного напряжения моста при условиях R₁ = R₂ = R₃ = R и R_x = (R+ΔR).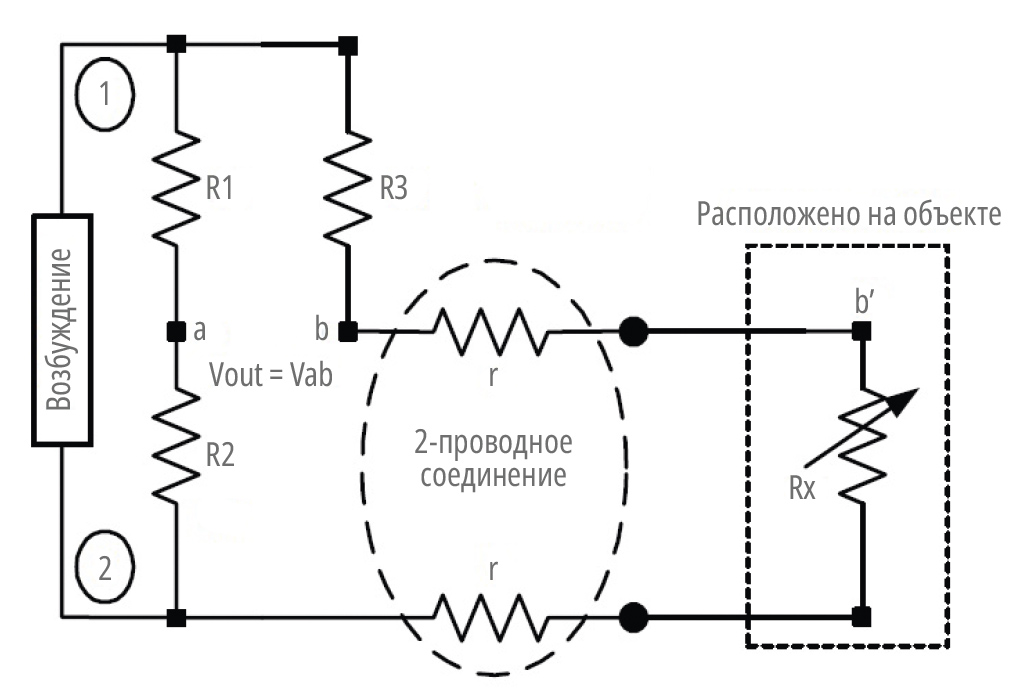


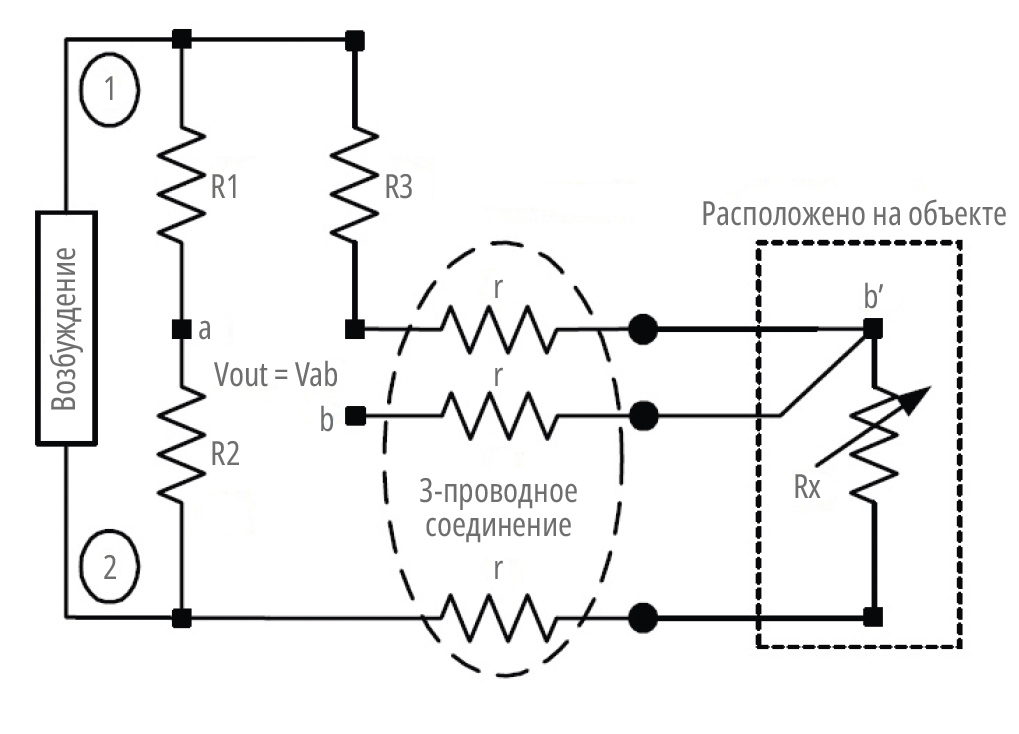
Возбуждение по напряжению равно V₁₂, а возбуждение по току Iexc, протекающему на клемму 1. Схема моста рассматривается всё та же, что на рис. 1, при этом не учитываются сопротивления линий выходного напряжения, а R_x = (R + ΔR).

Рис. 1. Уравнения (4-проводная схема категории 1)

Напряжение возбуждения V₁₂: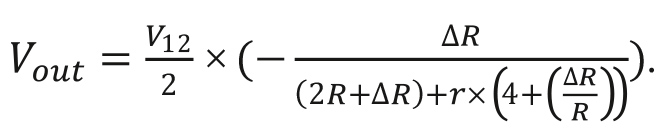

Ток возбуждения, при I_exc = V₁₂/R:

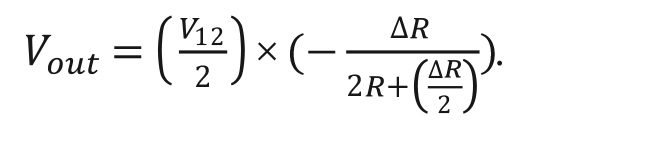
Рисунок 6. Уравнения (2-проводная схема категории 2)

Напряжение возбуждения V₁₂: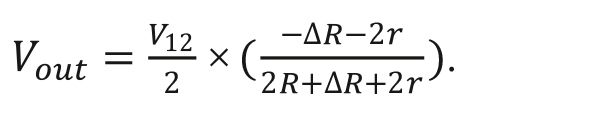



Ток возбуждения, при I_exc = V₁₂/R:

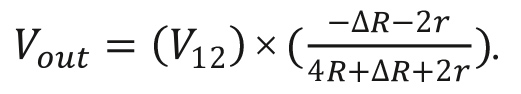
Рисунок 7. Уравнения (3-проводная схема категории 2)

Напряжение возбуждения V12: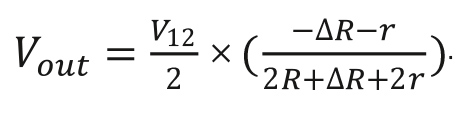



Ток возбуждения, при I_exc = V₁₂/R:

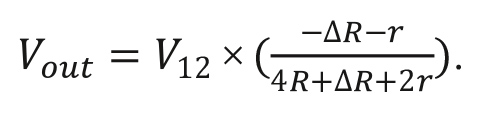
Выводы

На основе схем, приведённых на рис. 6 и 7, можно сделать следующие заклю­чения: 

1. выходное напряжение моста является нелинейной функцией от измеряемого параметра независимо от того, используется ли возбуждение током или напряжением;
2. при использовании токового возбуждения мостовая схема, относящаяся к категории 1, имеет выходные напряжения, которые не зависят от сопротивления линии;
3. выходные напряжения мостовой схемы категории 2 всегда зависят от сопротивления линии, независимо от того, используется ли возбуждение током или напряжением;
4. если (r << ∆R << R), т.е. сопротивлением линии всегда можно пренебречь, и если изменения сопротивления R_x очень малы по сравнению с R, то выход моста одинаков как для возбуждения по напряжению, так и по току.

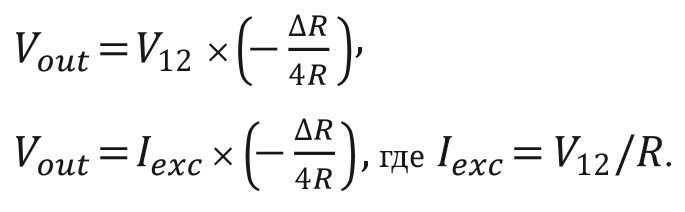
Ситуация, когда мостовая схема содержит более одного резистивного элемента с переменным сопротивлением при одинаковых по значению, но противоположных по знаку воздействиях, является обычной в мостовых измерениях.

Эти случаи обсуждаются в примечаниях по применению Dataforth для тензорезисторов.

На рис. 8 представлена блок-схема мостового модуля формирования сигнала Dataforth серии SCM5B38. Эти модули предназначены для взаимодействия с полными мостовыми схемами категории 1 с возможными опциями полумостовой и четвертьмостовой топологии категории 2. Преимущественное применение этого модуля приходится на промышленные тензоизмерительные приборы; тем не менее он хорошо подходит для любого контрольно-измерительного оборудования мостового типа.

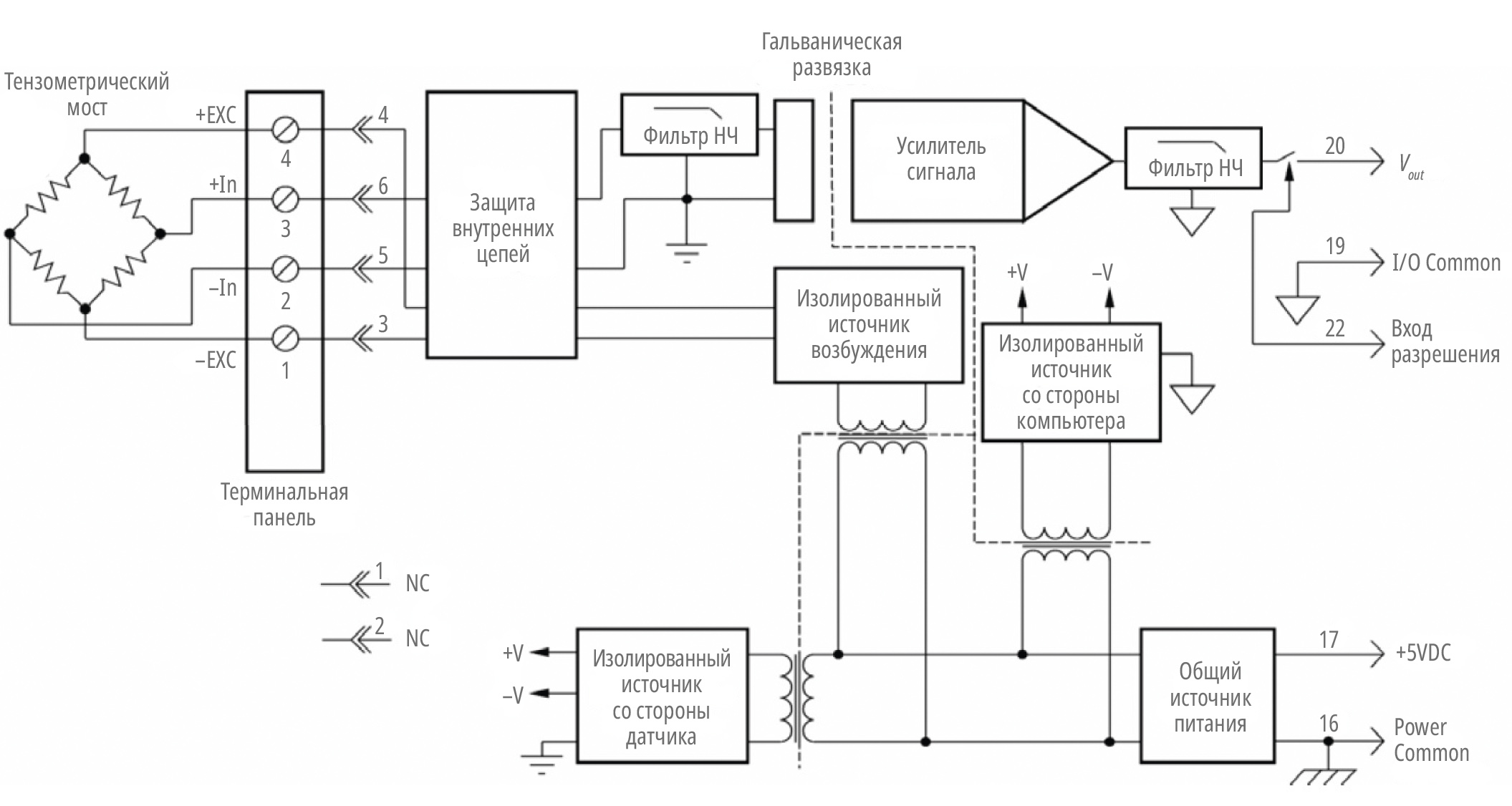
Модули серии SCM, такие как SCM5B38, SCM5B38, имеют несколько (обычно 5–7) полюсных фильтров с фильтрацией помех на стороне поля. Кроме того, эти модули имеют четырёхстороннюю изоляцию, которая включает прецизионную развязку питания для возбуждения поля, изолированное питание со стороны поля, изолированное питание со стороны системы и непосредственно изоляцию самого сигнала. Также модули имеют как узкополосные, так и широкополосные встроенные фильтры, что, в свою очередь, позволяет использовать их в различных сферах автоматизации и измерения. Кроме того, серия DSCA38 имеет регулировку нуля и настроек диапазона в пределах +/–5%. Регулировка нуля особенно полезна для балансировки мостовых схем. ● 

Автор – сотрудник фирмы ПРОСОФТ
Телефон: (495) 234-0636
E-mail: info@prosoft.ru

© СТА-ПРЕСС, 2024