Часть 2
Регулятор отношений
Задача регулировки отношений возникает, когда важно поддерживать не абсолютные значения параметров, а соотношение между ними. Например, если решается задача смешивания компонентов в заданных пропорциях, поддерживается горение с заданным процентным содержанием кислорода в горючей смеси и т.п.
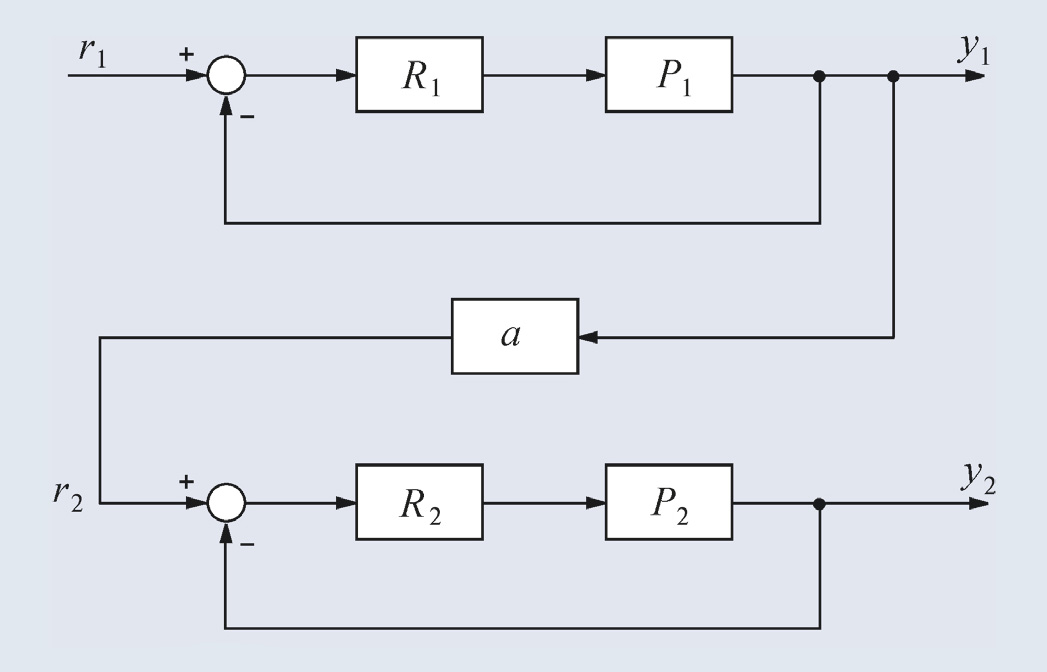
Пример решения данной задачи представлен на рис. 18 [5]. Первый регулятор поддерживает выходную величину y1 равной значению уставки r1. Значение уставки второго регулятора пропорционально регулируемой величине первого регулятора: r2(t) = ay1(t). Величина отношения устанавливается блоком a и может изменяться в соответствии с алгоритмом работы системы. Сигнал желательно брать именно с выхода системы y1 – это повышает точность, поскольку y1(t) отличается от r1(t) на величину погрешности, которая в динамике может быть значительной.
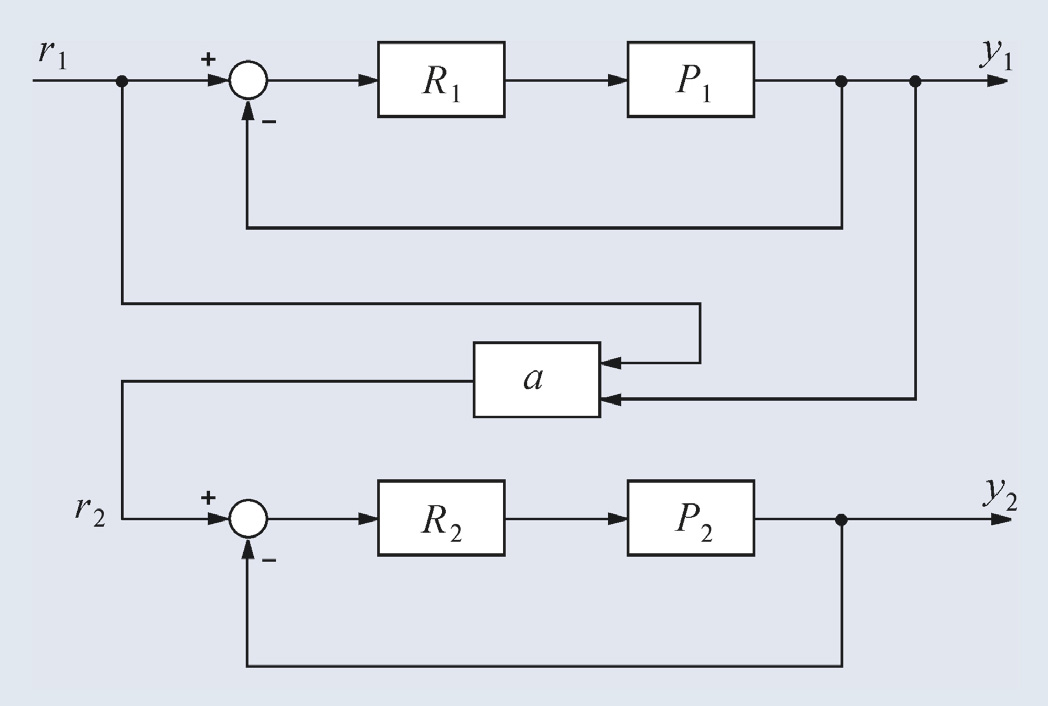
Кроме того, величина y1(t) всегда изменяется с некоторой задержкой относительно r1(t). Поэтому величина y2(t) будет отставать по времени от желаемого значения ay1(t). Смягчить данную проблему позволяет структура, показанная на рис. 19. Здесь блок a имеет два входа и описывается выражением:
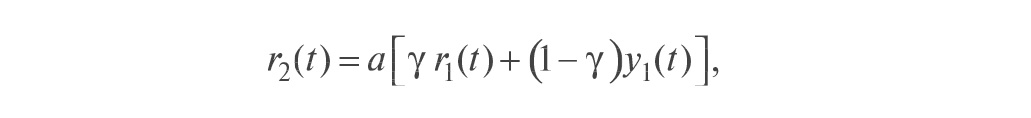
где γ – параметр, определяющий вклад r1(t) или y1(t) в величину r2(t). При γ = 0 эта структура идентична структуре, показанной на рис. 18.
Регулятор с внутренней моделью
Если модель М(s) объекта P(s) идентифицирована, то можно не рассчитывать параметры ПИД-регулятора, а использовать регулятор с показанной на рис. 20 структурой [9].
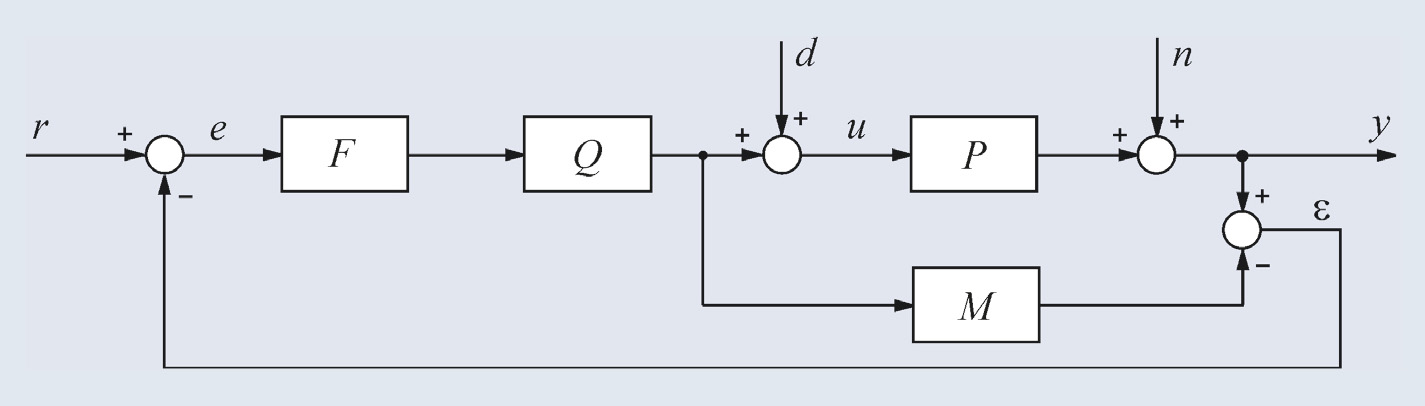
Здесь F(s) – фильтр, обычно выбираемый с передаточной функцией
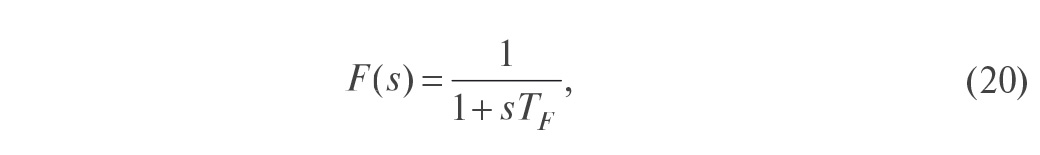
а Q – обращённая модель объекта, то есть Q(s) ≈ M–1(s). Знак приближённого равенства стоит потому, что обращение модели редко можно выполнить точно (см. раздел «Нахождение обратной динамики объекта»).
Для описания принципа действия регулятора, представленного на рис. 20, предположим сначала, что возмущения n и шумы измерений d отсутствуют, а модель объекта управления и обращённая модель являются точными, то есть
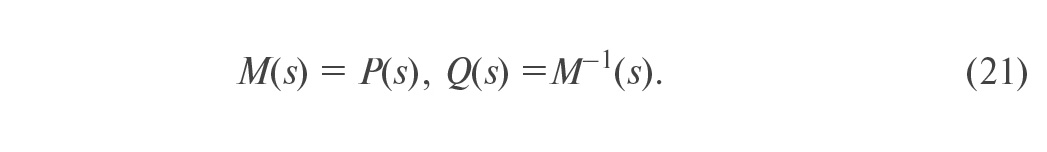
Тогда разность между сигналами на выходах процесса и модели равна нулю: ε = 0. Но в таком случае y = PQFr, и учитывая, что QP = 1 в силу (21), получим

Поскольку согласно (20) в установившемся режиме F(s) = 1, то в результате имеем y = r. Таким образом, регулятор с внутренней моделью точно поддерживает значение уставки в статическом режиме.
Фильтр нижних частот F(s) в такой структуре с помощью настройки граничной частоты 1/TF позволяет выбрать компромисс между запасом устойчивости и быстродействием замкнутой системы.
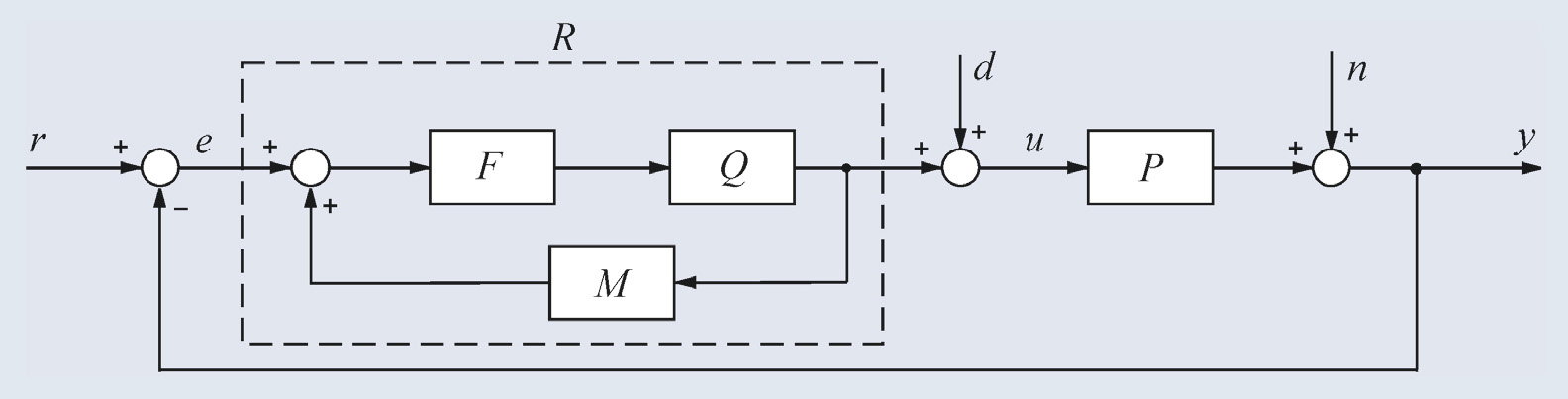
Регулятор, представленный на рис. 20, путём переноса блока вычисления разности ε может быть преобразован в эквивалентную классическую форму ПИД-регулятора (рис. 3, рис. 21), где
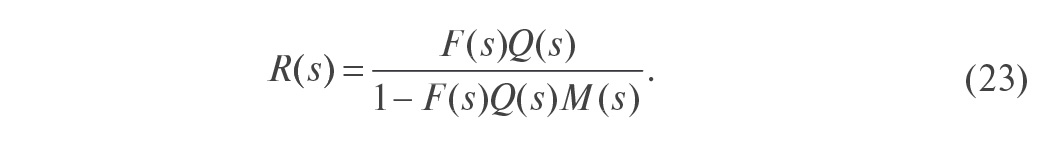
В общем случае регулятор (23) может иметь высокий порядок, который определяется порядком объекта.
Для объектов управления первого порядка регулятор с внутренней моделью полностью эквивалентен ПИД-регулятору, если задержку e–sL заменить Паде-аппроксимацией первого порядка [5].
Важной особенностью регулятора с внутренней моделью является возможность настройки робастности независимо от выбора остальных параметров регулятора. Для этого выбирают соответствующий фильтр F или параметр TF для фильтра первого порядка (20). Регулятор с внутренней моделью может дать очень хорошую реакцию на изменение уставки, однако реакция на внешние возмущения может быть слишком замедленной, поскольку в выражении (23) сокращаются нули и полюса передаточной функции [10].
Проектирование регулятора с внутренней моделью происходит следующим образом [9]. Сначала находят и оптимизируют обратную модель Q(s), исходя из требований к качеству переходного процесса при изменении уставки и не обращая внимания на робастность. Для получения начального приближения Q(s) предполагают, что M(s) = P(s), и используют методы обращения динамического оператора, описанные в разделе «Нахождение обратной динамики объекта». Единственным ограничением при оптимизации передаточной функции Q(s) является требование её асимптотической устойчивости. После этого выбирают структуру и параметры фильтра F(s), добиваясь требуемой робастности системы при заданном быстродействии. Поскольку в идеальном случае (22) свойства замкнутой системы определяются характеристикой выбранного фильтра, его граничная частота в этом случае определяет быстродействие всей замкнутой системы.
Для объектов, у которых транспортная задержка L составляет менее 0,25 от доминирующей постоянной времени объекта T, постоянную времени фильтра приближённо можно выбрать из диапазона 0,1T < TF < 0,5T [9]. Если 0,25 < L < 0,75, то TF ≈ 1,5(L +T). Если транспортная задержка ещё больше, то постоянную времени фильтра увеличивают далее, выбирая в качестве начального приближения TF = 3(L+T) [9].
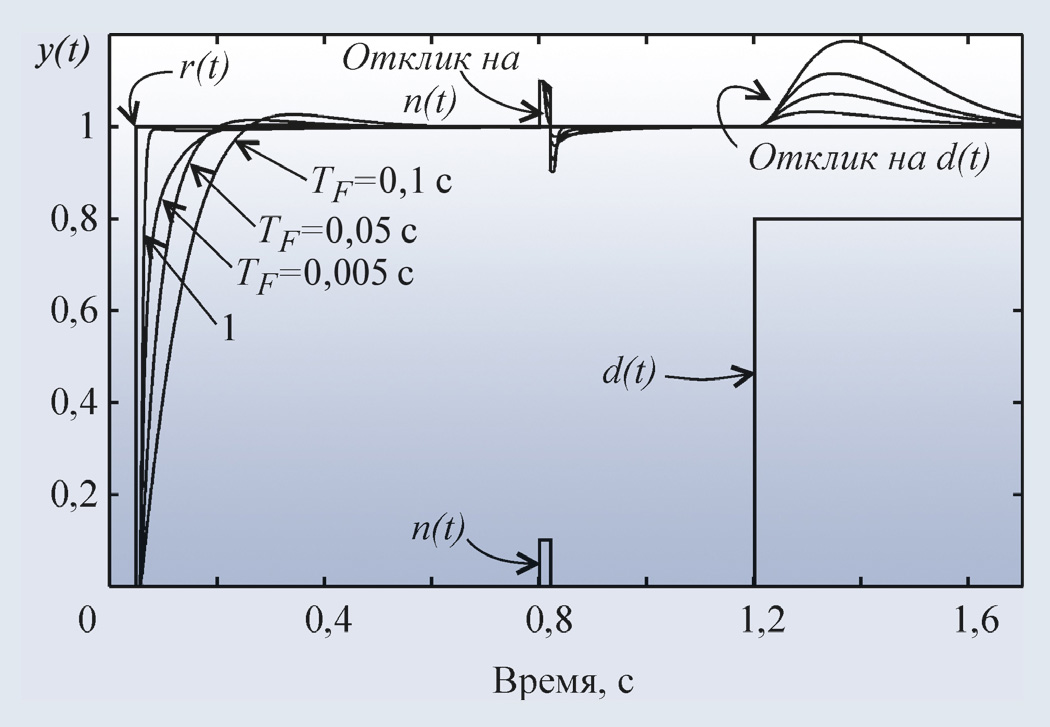
Пример реакции системы со встроенной моделью на изменение уставки r(t), импульс помехи n(t) и возмущение d(t) приведён на рис. 22. Объект описывается передаточной функцией вида
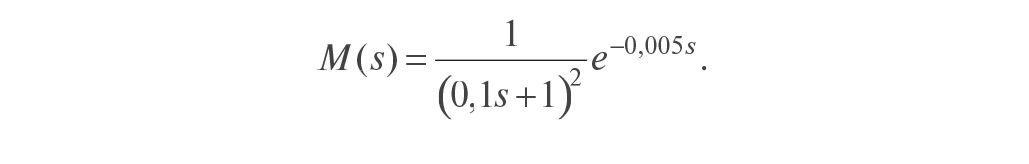
Модель описывается передаточной функцией
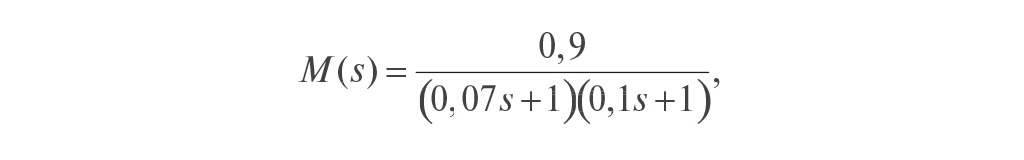
то есть модель не точно соответствует объекту. Обратный оператор
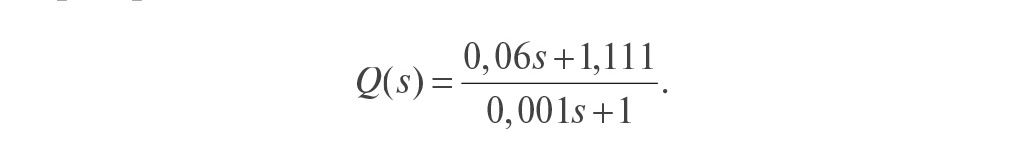
Отметим, что для обеспечения точности в установившемся режиме должно выполняться соотношение Q(0)M(0) = 1, поскольку коэффициент передачи регулятора в установившемся режиме должен стремиться к бесконечности (23). На рис. 22 кривая 1 соответствует случаю, когда модель точно соответствует объекту, а постоянная времени фильтра TF = 0,05 мс. Как видим, повышение точности модели и уменьшение постоянной времени фильтра позволяют существенно увеличить быстродействие системы, однако реакция на возмущающие воздействия при этом изменяется слабо.
ПИД-регуляторы для систем с транспортной задержкой. Предиктор Смита
Типовая переходная характеристика объекта управления, в котором происходит перенос тепла, показана на рис. 23. После задержки длительностью L происходит плавное нарастание температуры.
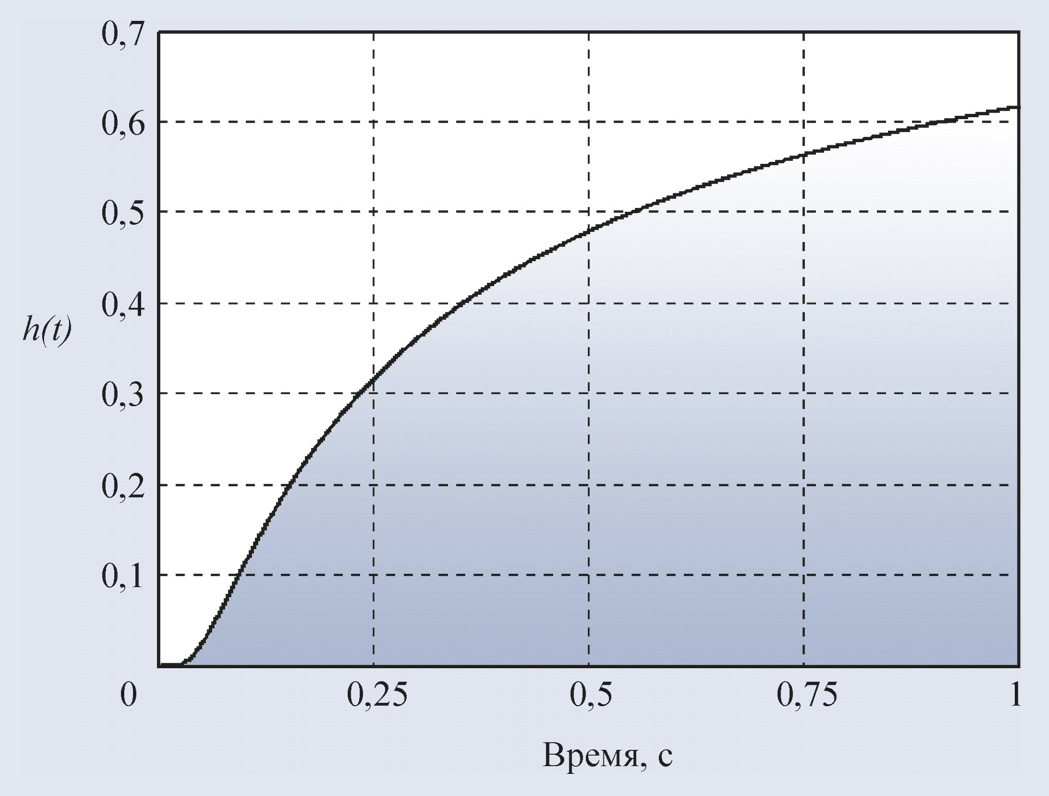
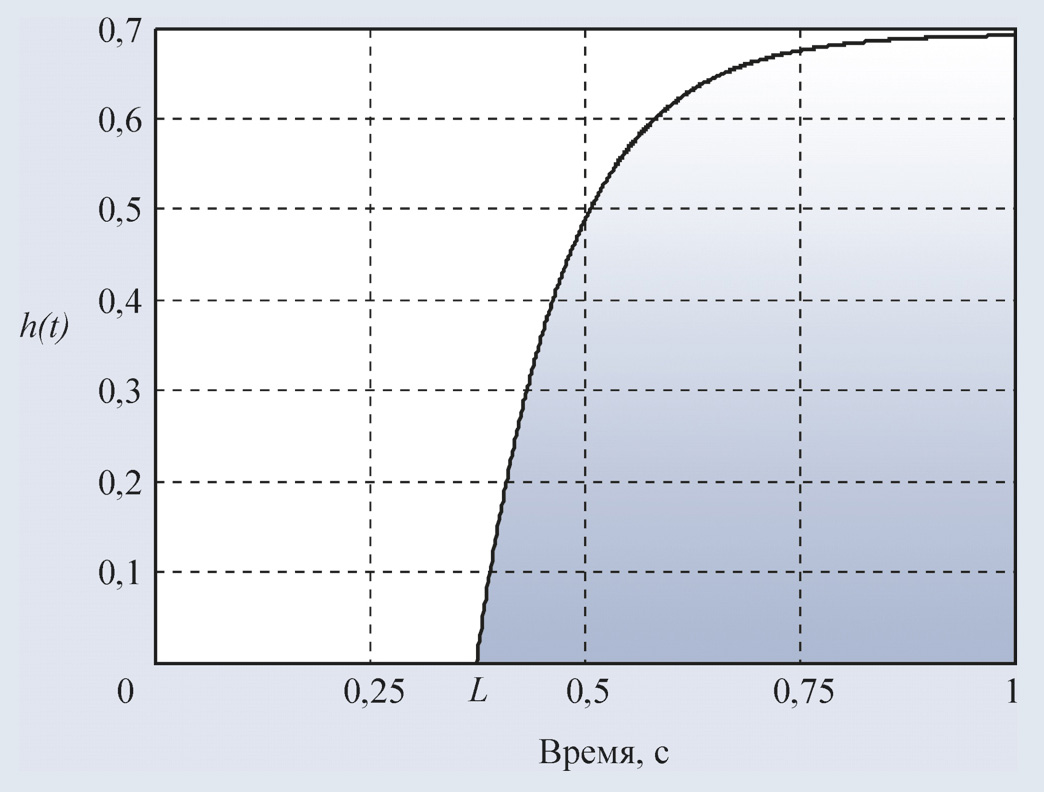
Существуют также объекты, в которых транспортная задержка может быть как угодно большой по сравнению с длительностью переходного процесса (рис. 24). Примером могут служить процессы, связанные с перемещением тел в пространстве, обычно с транспортировкой по трубам и транспортёрным лентам.
Поскольку у звена с транспортной задержкой сдвиг фаз ϕ = –ωL увеличивается с ростом величины задержки L, а частота ω180 увеличивается с уменьшением длительности переходного процесса L+T, то отношение L/(L+T) характеризует сложность управления объектом.
Предиктор Смита
Для управления объектами с большой транспортной задержкой, обычно при
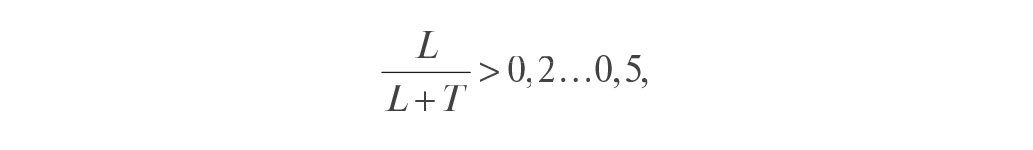
используют специальные структуры ПИД-регуляторов, содержащие блоки для предсказания поведения объекта через время L (предикторы, от английского слова “prediction”). Структура такого регулятора была предложена Смитом в 1957 году [11] и иногда называется предиктором Смита. Предиктор Смита включён в некоторые промышленные ПИД-регуляторы.
Цель предиктора Смита – предсказать, какой сигнал должен появиться на выходе объекта до того, как он там появится на самом деле. Для предсказания можно использовать модель объекта управления, состоящую из дробно-рациональной части Mo и транспортной задержки e–sL. Благодаря тому что из модели можно исключить задержку, появляется принципиальная возможность предсказания поведения объекта до появления сигнала на его выходе.
Реализуется эта возможность системой со структурой, показанной на рис. 25. Здесь R – обычный ПИД-регулятор, Poe–sL – передаточная характеристика объекта управления.
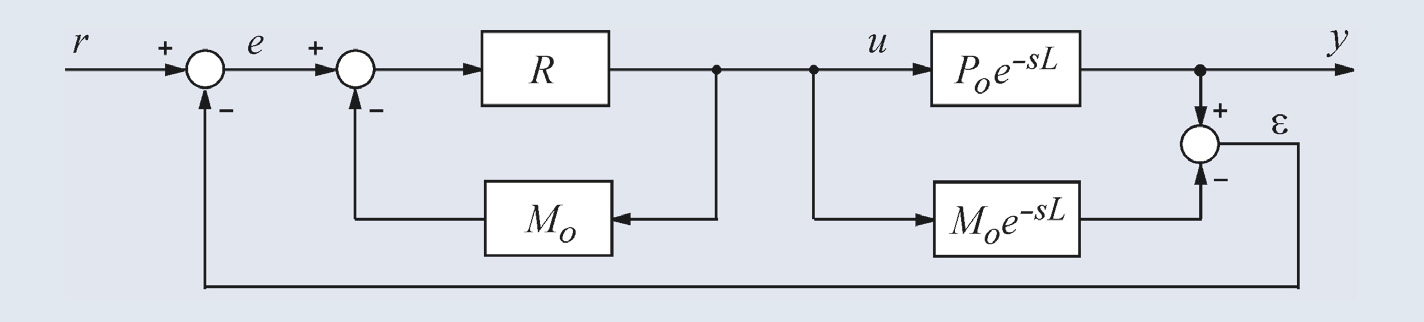
Принцип работы системы состоит в следующем. Предположим, что модель абсолютна точна. Тогда разность сигналов на выходах модели и объекта будет равна нулю (ε = 0). Но в таком случае непосредственно из схемы на рис. 25 можно получить:
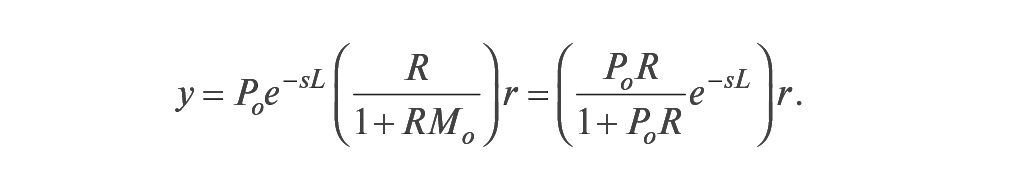
В этом выражении член PoR/(1+PoR) представляет собой передаточную функцию системы без транспортной задержки. А это значит, что звено с транспортной задержкой не входит в контур обратной связи и не влияет на устойчивость и быстродействие системы, то есть происходит регулирование в контуре с моделью без задержки, а транспортная задержка только добавляется к полученному результату.
Рассмотрим теперь работу предиктора Смита без предположения ε = 0. В этом случае схему на рис. 25 можно описать следующими уравнениями:
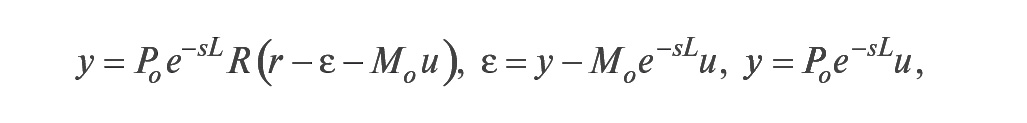
откуда можно найти
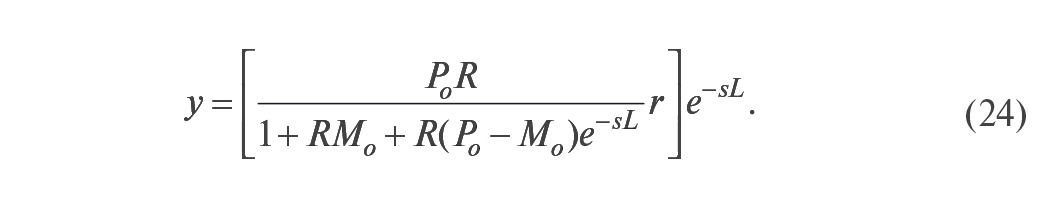
Как видим, с ростом точности модели разность (Po – Mo) в знаменателе стремится к нулю и из передаточной функции системы исключается транспортная задержка, которая только добавляется к уже полученному результату регулирования (в квадратных скобках (24)).
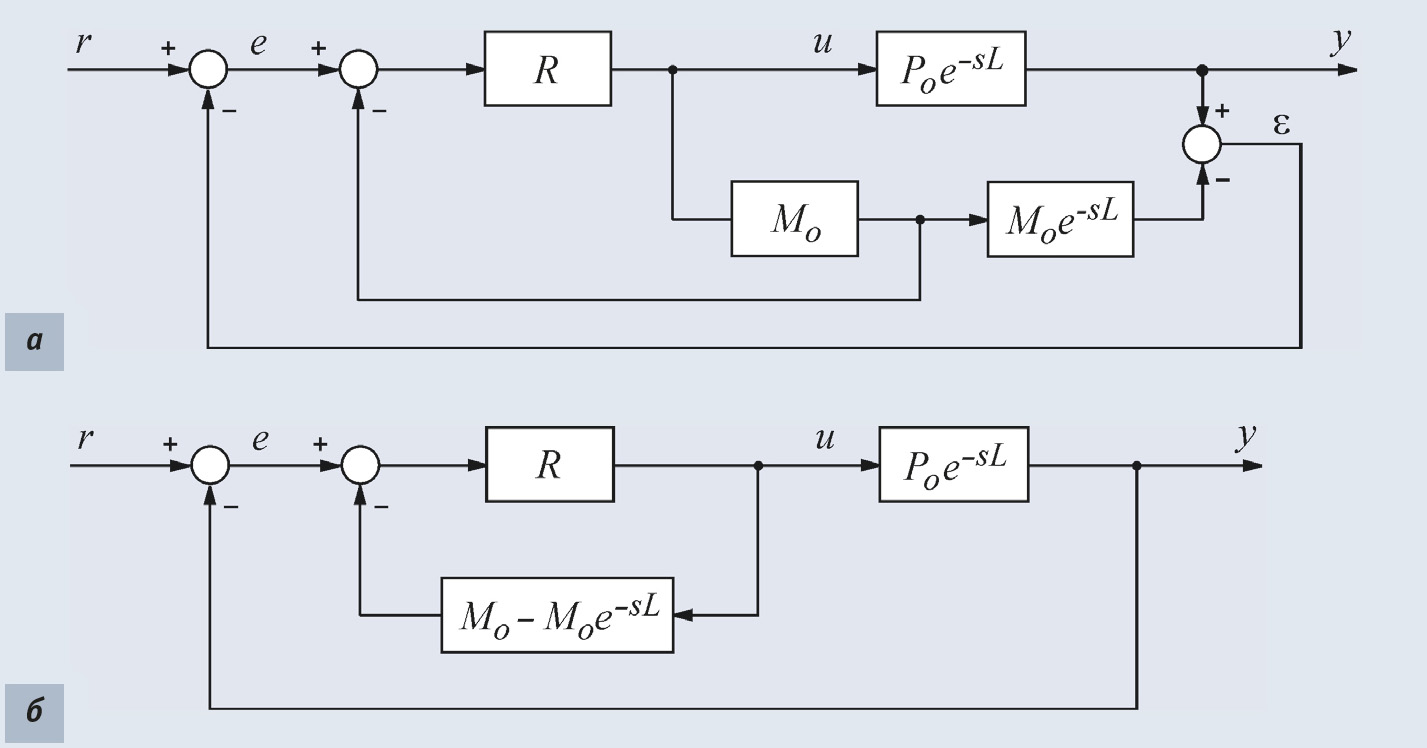
С помощью топологических преобразований структурных схем можно получить много эквивалентных между собой структур систем с предиктором Смита. Две из них представлены на рис. 26. Можно показать, что они описываются тем же уравнением (24).
ППИ-регуляторы
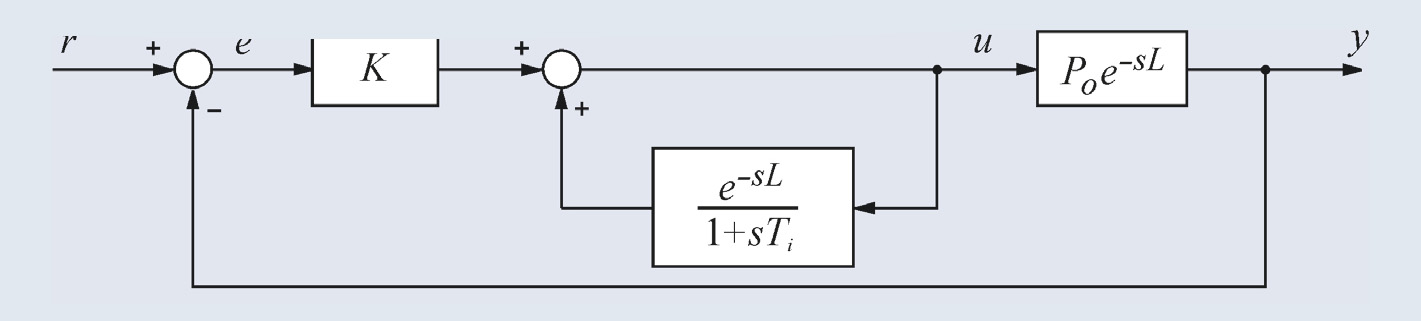
ППИ-регулятор (сокращение от «Предиктивный ПИ») является модификацией предиктора Смита, которая распространена в АСУ ТП более широко, чем сам предиктор Смита. Один из вариантов ППИ-регулятора представлен на рис. 27 [9]. Существует много модификаций структуры, изображённой на рис. 27, например, см. [5].
Нечёткая логика, нейронные сети и генетические алгоритмы
ПИД-регуляторы, описанные в предыдущих разделах, имеют плохие показатели качества при управлении нелинейными и сложными системами, а также при недостаточной информации об объекте управления. Характеристики регуляторов в этих случаях можно улучшить с помощью методов нечёткой (фаззи-) логики, нейронных сетей и генетических алгоритмов. Перечисленные методы за рубежом называют “soft-computing”, подчеркивая их отличие от “hard-computing”, состоящее в возможности оперировать с неполными и неточными данными. В одном контроллере могут применяться комбинации перечисленных методов (фаззи-ПИД, нейро-ПИД, нейро-фаззи-ПИД-регуляторы с генетическими алгоритмами).
Основным недостатком нечётких и нейросетевых контроллеров является сложность их настройки (составления базы правил и обучения нейронной сети).
Нечёткая логика в ПИД-регуляторах
Нечёткое управление (управление на основе методов теории нечётких множеств) [12] используется при недостаточном знании объекта управления, но наличии опыта управления им, в нелинейных системах, идентификация которых слишком трудоёмка, а также в случаях, когда по условию задачи необходимо использовать знания эксперта. Примером может быть доменная печь или ректификационная колонна, математическая модель которых содержит много эмпирических коэффициентов, изменяющихся в широком диапазоне и вызывающих большие затруднения при идентификации [12]. В то же время квалифицированный оператор достаточно хорошо управляет такими объектами, пользуясь показаниями приборов и накопленным опытом.
ПИД-регуляторы с нечёткой логикой в настоящее время используются в коммерческих системах для наведения телекамер при трансляции спортивных событий, в системах кондиционирования воздуха, при управлении автомобильными двигателями, для автоматического управления двигателем пылесоса и в других областях.
Поскольку информация, полученная от оператора, выражена словесно, для её использования в ПИД-регуляторах применяют лингвистические переменные и аппарат теории нечётких множеств, который был разработан Л. Заде в 1965 году [13]. Основная идея этой теории состоит в следующем. Если в теории чётких множеств некоторый элемент (например, температура 50 градусов) может принадлежать множеству (например, множеству «температура горячей воды Тгор.») или не принадлежать ему, то в теории нечётких множеств вводится понятие функции принадлежности, которая характеризует степень принадлежности элемента множеству. При этом говорят, например, «температура 50 градусов принадлежит множеству Тгор. со степенью принадлежности 0,264». Функцию принадлежности можно приближённо трактовать как вероятность того, что данный элемент принадлежит множеству [14], однако такая интерпретация, хотя и является для инженеров более понятной, не является математически строгой, поскольку существующая теория нечётких множеств не оперирует понятием вероятности.
В 1974 году Мамдани [15] показал возможность применения идей нечёткой логики для построения системы управления динамическим объектом, а годом позже вышла публикация Мамдани (Mamdani) и Assilian, в которой описывался нечёткий ПИ-регулятор и его применение для управления парогенератором. С тех пор область применения нечётких регуляторов постоянно расширяется, увеличивается разнообразие их структур и выполняемых функций.
Нечёткая логика в ПИД-регуляторах используется преимущественно двумя путями: для построения самого регулятора и для организации подстройки коэффициентов ПИД-регулятора. Оба пути могут использоваться в ПИД-контроллере одновременно.
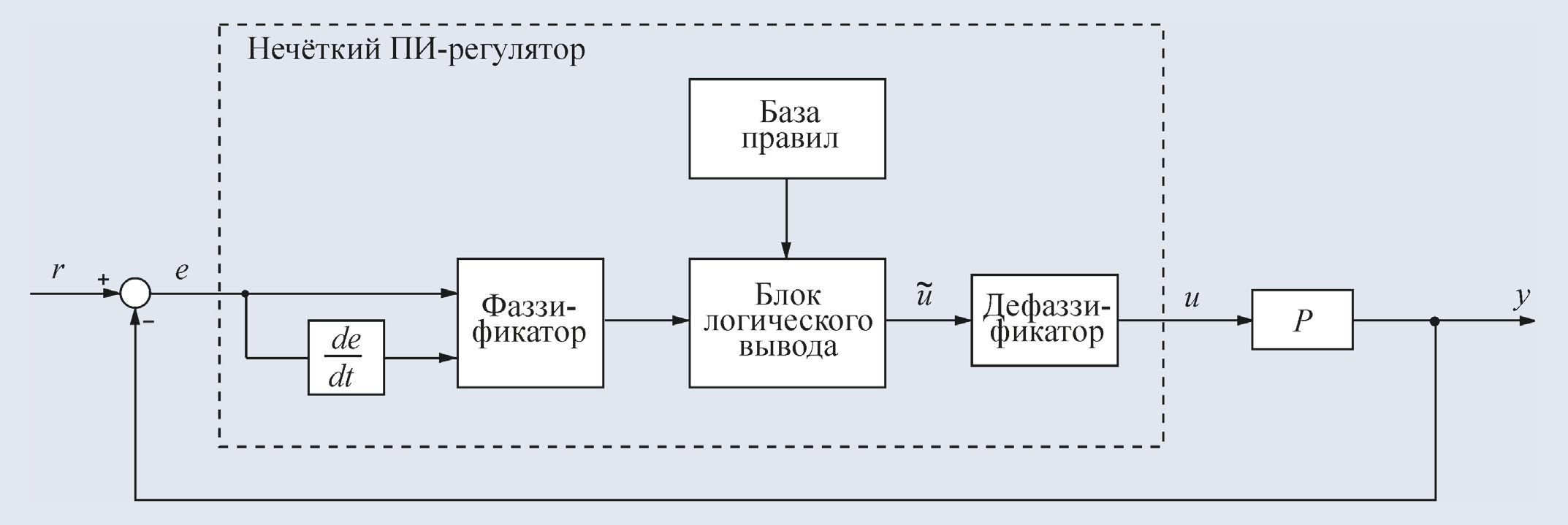
Одна из наиболее распространённых структур нечёткого регулятора (нечёткого ПИ-регулятора) показана на рис. 28. На вход регулятора поступает ошибка e, которая используется для вычисления производной по времени de/dt. Обе величины сначала подвергаются операции фаззификации (преобразования в нечёткие переменные, от английского слова fuzzy – нечёткий), затем полученные нечёткие переменные используются в блоке нечёткого логического вывода для получения управляющего воздействия на объект, которое после выполнения операции дефаззификации (обратного преобразования нечётких переменных в чёткие) поступает на выход регулятора в виде управляющего воздействия u.
Принципы построения нечёткого ПИ-регулятора
Для применения методов нечёткой логики прежде всего необходимо преобразовать обычные чёткие переменные в нечёткие. Процесс фаззификации иллюстрируется рис. 29.
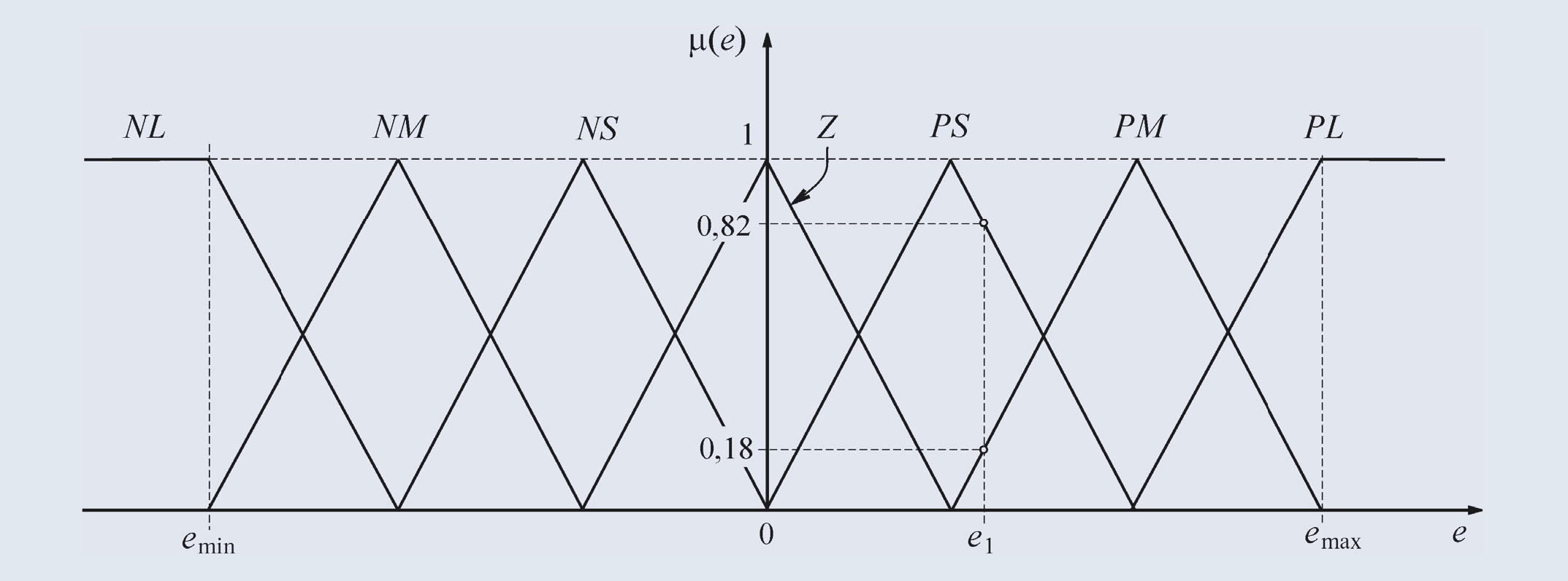
Диапазон изменения переменной e разбивается на множества (подмножества) NL, NM, NS, Z, PS, PM, PL, в пределах каждого из которых строится функция принадлежности переменной e каждому из множеств. На рис. 29 функции принадлежности имеют треугольную (наиболее распространённую) форму, хотя в общем случае они могут быть любыми, исходя из смысла решаемой задачи [12]. Количество множеств также может быть произвольным. Для нечётких множеств существует общепринятая система обозначений: N – отрицательный (Negative), Z – нулевой (Zero), P – положительный (Positive); к этим обозначениям добавляют буквы S (Small – малый), М (Medium – средний), L (Large – большой). Например, NL – отрицательный большой, NM – отрицательный средний, PL – положительный большой. Количество переменных (термов) может быть любым, однако с увеличением их числа существенно возрастают требования к опыту эксперта, который должен сформулировать правила для всех комбинаций входных переменных.
Если величина ошибки e на входе нечёткого регулятора (рис. 28) равна e1 (рис. 29), то соответствующее значение нечёткой переменной будет равно PS со степенью принадлежности подмножеству PS, равной μ(e1) = 0,82 или будет равно PM со степенью принадлежности μ(e1) = 0,18. Степень принадлежности ошибки e1 другим множествам (Z, PL, NS и др.) равна нулю. Таким образом, величина ошибки e1 оказалась преобразованной в нечёткие переменные. Для выполнения функции регулирования над нечёткими переменными должны быть выполнены операции, построенные на основании высказываний оператора, сформулированных в виде нечётких правил. Совокупность нечётких правил и нечётких переменных используется для осуществления нечёткого логического вывода (рис. 28), результатом которого является управляющее воздействие на объект управления.
Нечёткий вывод выполняется следующим образом. Предположим, что область изменения ошибки e разделена на множества N, Z, P, область изменения управляющего воздействия – на множества NL, NM, Z, PM, PL и что с помощью эксперта удалось сформулировать следующие правила работы регулятора [5]:
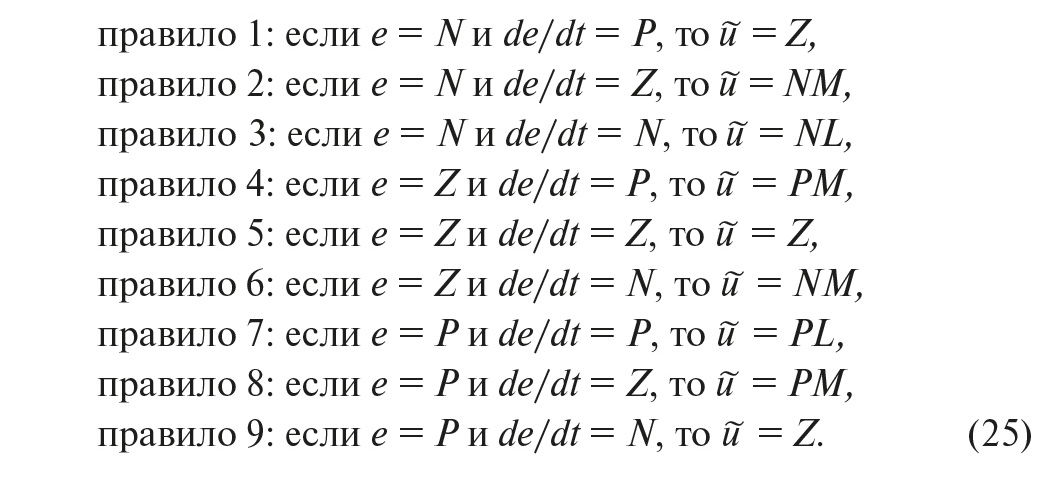
Приведённые правила часто записывают в более компактной табличной форме (рис. 30).
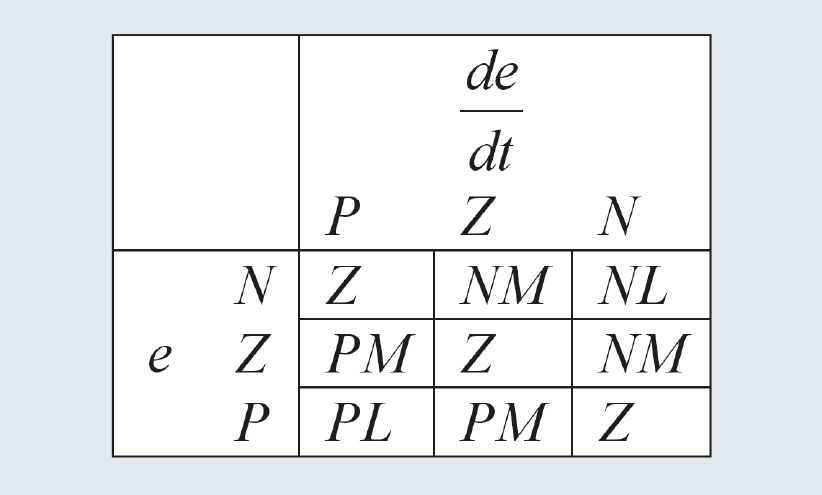
Используя правила, можно получить значение управляющей переменной u~ на выходе нечёткого регулятора. Для этого нужно найти функцию принадлежности переменной u~ множеству, образованному в результате выполнения операций вывода над множествами, входящими в систему правил (25). Операция И в правилах (25) соответствует пересечению множеств, а результат применения всех правил соответствует операции объединения множеств [12]. Функция принадлежности для пересечения двух множеств, например N и P (правило 1), находится как
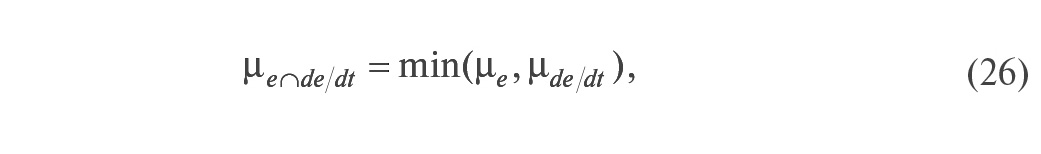
то есть каждое значение функции принадлежности пересечения множеств равно наименьшему значению из двух, стоящих в выражении (26) в круглых скобках [16].Функция принадлежности для объединения тех же множеств имеет вид [16]:
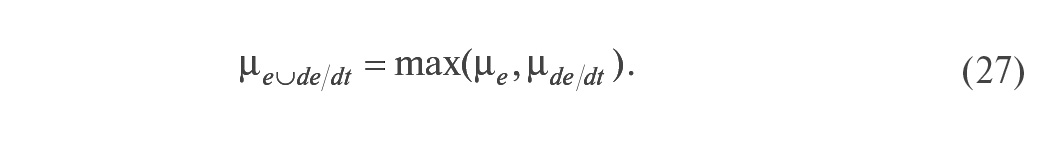
Функции принадлежности, полученные при пересечении или объединении множеств, могут быть определены различными способами, в зависимости от смысла решаемой задачи. В этом смысле сама теория нечётких множеств тоже является нечёткой. В [17] приводится 10 различных определений функции принадлежности для пересечения множеств, но не сказано, какое из них нужно выбрать для решения конкретной задачи. Используют, в частности, более понятную операцию нахождения функций принадлежности в случае пересечения и объединения множеств, имеющую аналогию с правилами умножения и сложения вероятностей:
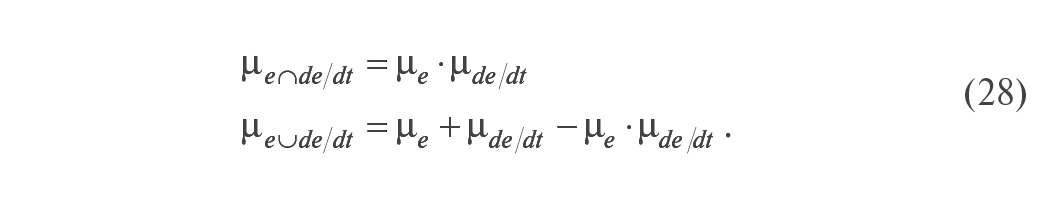
Однако применение первых двух способов нахождения функции принадлежности обычно более предпочтительно, так как при этом сохраняется большинство правил, разработанных для обычных множеств [16].
Функции принадлежности для каждого из множеств NL, NM, Z, PM, PL, входящих в нечёткую переменную u~ в правилах (25), получаются в виде [17]:
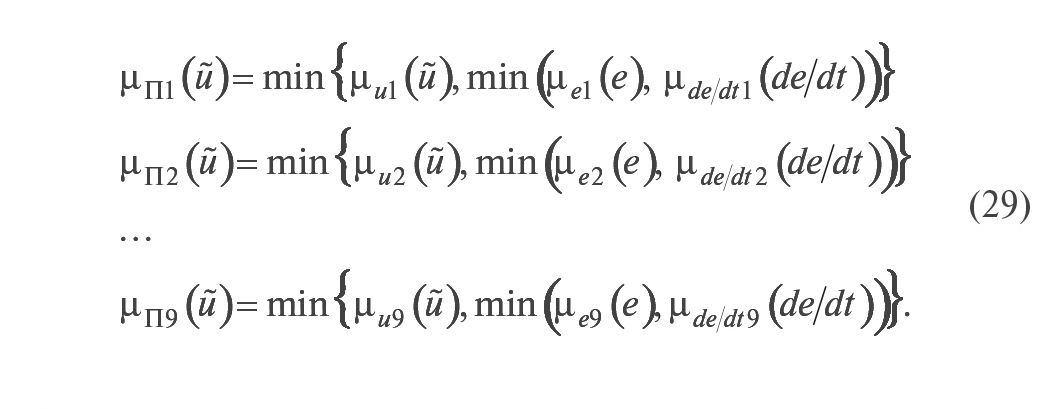
Здесь каждое из девяти уравнений соответствует одному из правил (25). Результирующая функция принадлежности управляющего воздействия u~, полученная после применения всех 9 правил, находится в соответствии с (27) как объединение функций принадлежности всех правил (25):
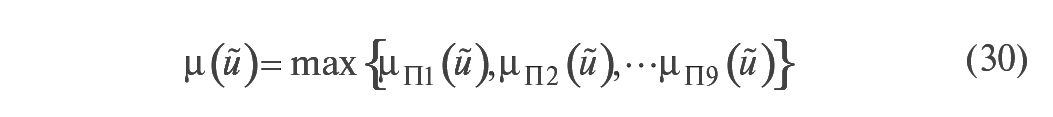
Теперь, когда получена результирующая функция принадлежности управляющего воздействия u, возникает вопрос, какое конкретно значение управляющего воздействия нужно выбрать. Если использовать вероятностную интерпретацию теории нечётких множеств, то становится понятно, что такое значение можно получить по аналогии с математическим ожиданием управляющего воздействия в виде:
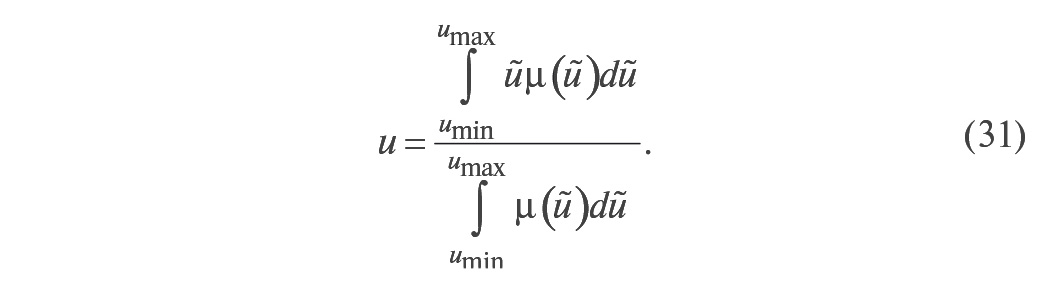
Такой способ дефаззификации является наиболее распространённым, но не единственным. Для построения нечётких регуляторов обычно используют П, И, ПИ, ПД, ПД(И), ПИ(Д) и ПИД-законы регулирования [18]. В качестве входных сигналов для системы нечёткого вывода используют сигнал ошибки, приращение ошибки, квадрат ошибки и интеграл от ошибки [18]. Реализация нечёткого ПИД-регулятора вызывает проблемы, поскольку он должен иметь трёхмерную таблицу правил в соответствии с тремя слагаемыми в уравнении ПИД-регулятора, которую чрезвычайно сложно заполнить, пользуясь ответами эксперта. Большое количество структур нечётких ПИД-контроллеров можно найти в статье [18].Окончательная настройка нечёткого регулятора или настройка, близкая к оптимальной, до сих пор остаётся трудной задачей. Для этого используются генетические поисковые методы, требующие больших вычислительных ресурсов и времени.
Применение нечёткой логики для подстройки коэффициентов ПИД-регулятора
Настройка ПИД-регулятора по формулам обычно не является оптимальной и может быть улучшена с помощью дальнейшей подстройки. Подстройка может быть выполнена оператором на основании эвристических правил или автоматически, с помощью блока нечёткой логики (рис. 31). Блок нечёткой логики (фаззи-блок) использует базу правил и методы нечёткого вывода. Фаззи-подстройка позволяет уменьшить перерегулирование, снизить время установления и повысить робастность ПИД-регулятора [19].
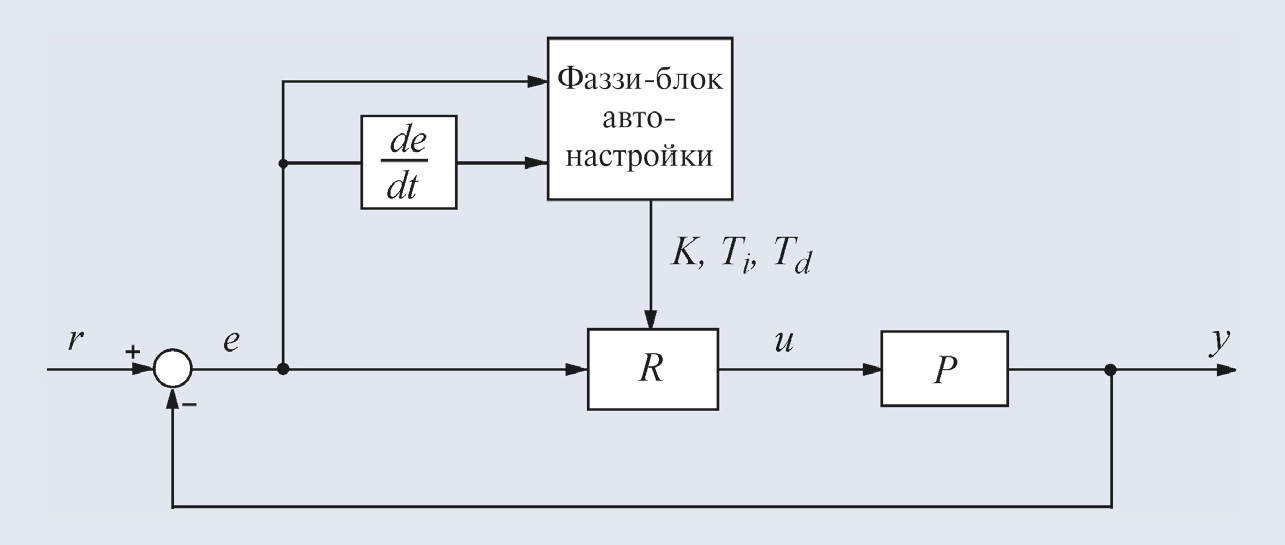
Процесс автонастройки регулятора с помощью блока нечёткой логики начинается с поиска начальных приближений коэффициентов регулятора K, Ti, Td. Обычно это делается методом Зиглера-Никольса, исходя из периода собственных колебаний в замкнутой системе и петлевого усиления. Далее формулируется критериальная функция, необходимая для поиска оптимальных значений параметров настройки методами оптимизации.
В процессе настройки регулятора используется несколько шагов [20]. Сначала выбираются диапазоны входных и выходных сигналов тюнера (блока автонастройки), форма функций принадлежности искомых параметров, правила нечёткого вывода, механизм логического вывода, метод дефаззификации и диапазоны масштабных множителей, необходимых для пересчёта чётких переменных в нечёткие. Поиск параметров регулятора выполняется методами оптимизации. Для этого выбирается целевая функция как интеграл от суммы квадратов ошибки регулирования и времени установления. В критерий минимизации иногда добавляют скорость нарастания выходной переменной объекта.
В качестве искомых параметров (параметров, которые надо найти) выбирают положение максимумов функций принадлежности и масштабные коэффициенты на входе и выходе фаззи-блока. К задаче оптимизации добавляют ограничения на диапазон изменения позиции функций принадлежности. Оптимизация критериальной функции может быть выполнена, например, с помощью генетических алгоритмов.
Следует отметить, что в случаях, когда информации достаточно для получения точной математической модели объекта, традиционный регулятор всегда будет лучше нечёткого потому, что при синтезе нечёткого регулятора исходные данные заданы приближённо.
Искусственные нейронные сети в ПИД-регуляторах
Нейронные сети, как и нечёткая логика, используются в ПИД-регуляторах двумя путями: для построения самого регулятора и для построения блока настройки его коэффициентов. Особенностью нейронной сети является способность к «обучению», что позволяет передать нейронной сети опыт эксперта. Регулятор с нейронной сетью похож на регулятор с табличным управлением, однако отличается специальными методами настройки («обучения»), разработанными для нейронных сетей, и методами интерполяции данных.
В отличие от нечёткого регулятора, где эксперт должен сформулировать правила настройки в лингвистических переменных, при использовании нейронной сети от эксперта не требуется формулировки правил – достаточно, чтобы он несколько раз сам настроил регулятор в процессе «обучения» нейронной сети.
Нейронные сети были предложены в 1943 году Мак-Каллоком и Питтсом как результат изучения нервной деятельности и биологических нейронов. Искусственный нейрон представляет собой функциональный блок с одним выходом y и n входами x1, x2,…xn, который реализует в общем случае нелинейное преобразование
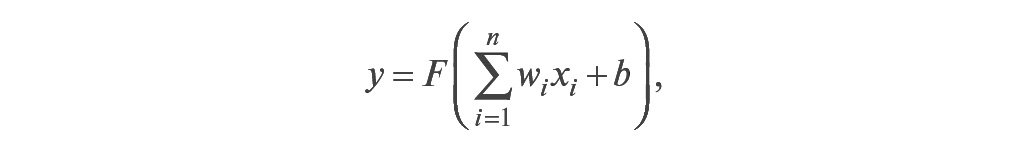
где wi – весовые коэффициенты (параметры) при входных переменных xi; b – постоянное смещение; F(•) – функция активации нейрона. Функция активации может иметь, например, такой вид: F(ζ) = 1/(1 + exp(–aζ)) — сигмоидальная функция с некоторым параметром a.
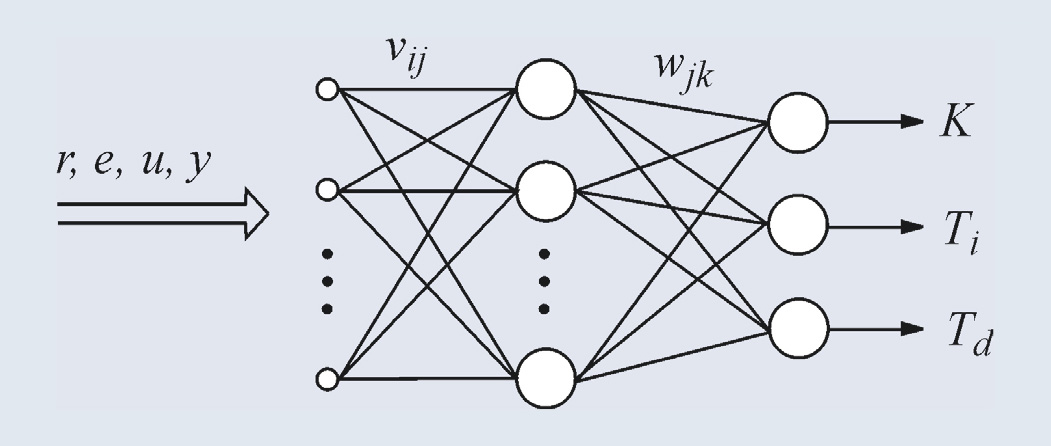
Нейронная сеть (рис. 32) состоит из множества связанных между собой нейронов, количество связей может составлять тысячи. Благодаря нелинейности функций активации и большому количеству настраиваемых коэффициентов (в работе [21] использовано 35 нейронов во входном слое и 25 – в выходном, при этом количество коэффициентов составило 1850) нейронная сеть может выполнять достаточно точно нелинейное отображение множества входных сигналов во множество выходных.
Типовая структура системы автоматического регулирования с ПИД-регулятором и нейронной сетью в качестве блока автонастройки показана на рис. 33 [21, 22]. Нейронная сеть NN в данной структуре играет роль функционального преобразователя, который для каждого набора сигналов r, e, u, y вырабатывает коэффициенты ПИД-регулятора K, Ti, Td.
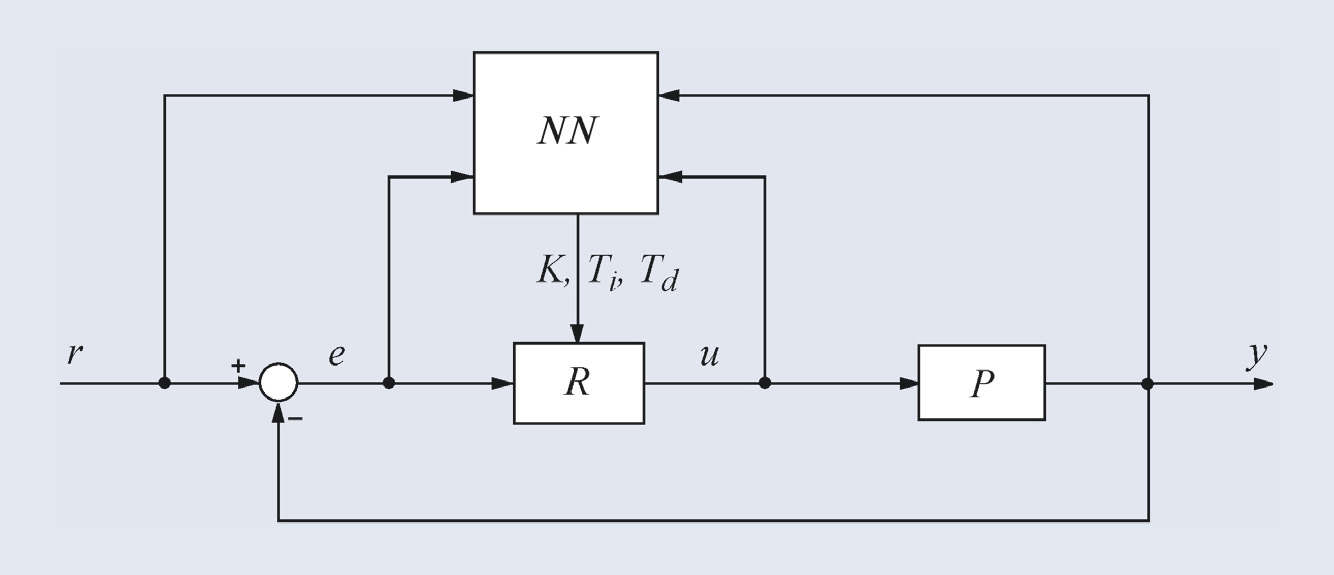
Самой сложной частью в проектировании регуляторов с нейронной сетью является процедура «обучения» сети. «Обучение» заключается в идентификации неизвестных параметров нейронов wi, b и a. Для «обучения» нейронной сети обычно используют методы градиентного поиска минимума критериальной функции ε = (u* – u)2, зависящей от параметров нейронов. Процесс поиска является итерационным, на каждой итерации находят все коэффициенты сети, сначала для выходного слоя нейронов, затем предыдущего и так до первого слоя (метод обратного распространения ошибки) [17]. Используются также другие методы поиска минимума, в том числе генетические алгоритмы, метод моделирования отжига, метод наименьших квадратов.
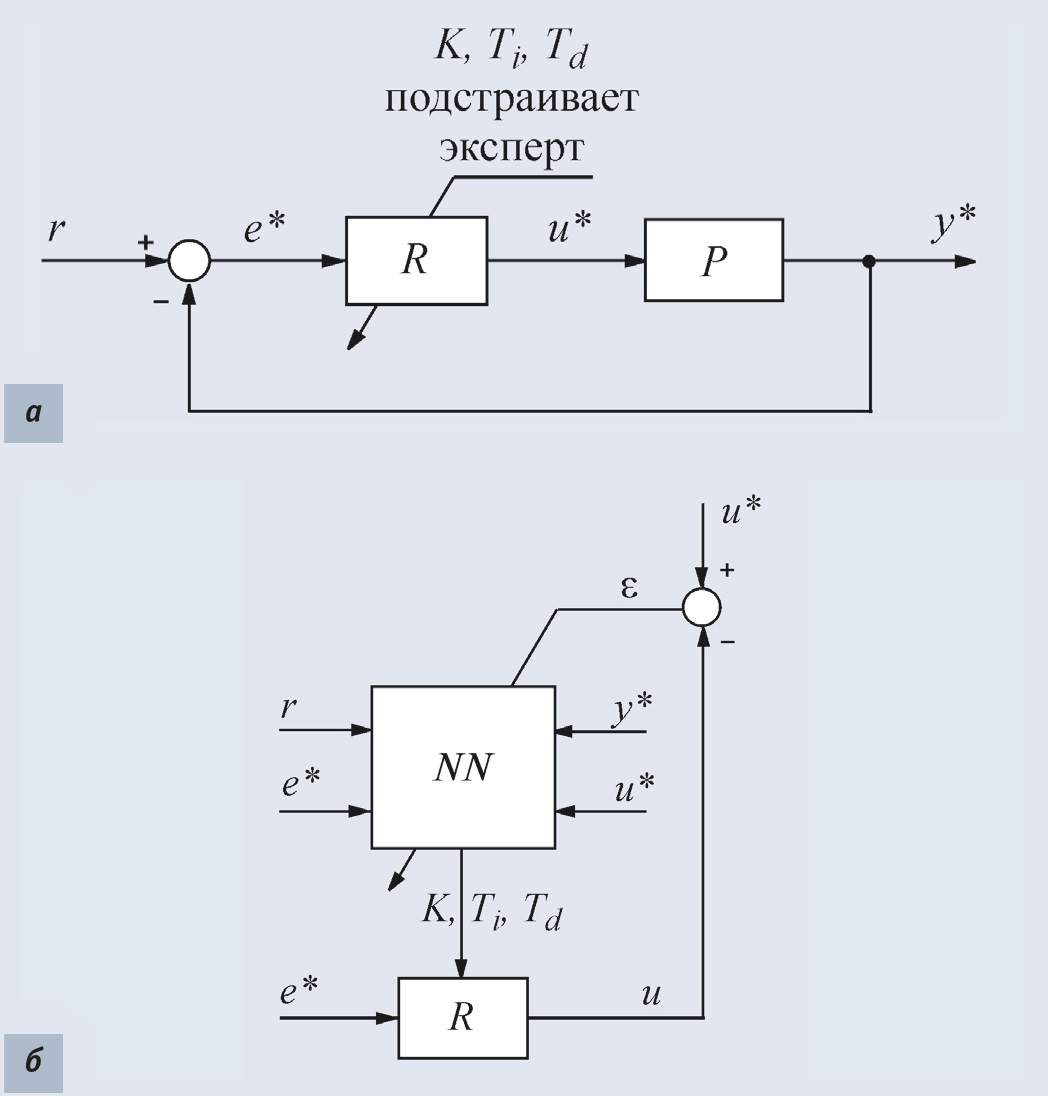
Процесс «обучения» нейронной сети выглядит следующим образом (рис. 34). Эксперту предоставляют возможность подстраивать параметры регулятора K, Ti, Td в замкнутой системе автоматического регулирования при различных входных воздействиях r(t). Предполагается, что эксперт умеет это делать с достаточным для практики качеством. Временные диаграммы (осциллограммы) переменных r*, e*, u*, y*, полученные в подстраиваемой экспертом системе (рис. 34 а), записываются в архив и затем подаются на нейронную сеть, подключённую к ПИД-регулятору (рис. 34 б). Нейронная сеть настраивается таким образом, чтобы минимизировать погрешность ε = (u* – u)2 между сигналом u*, полученным с участием эксперта, и сигналом u, полученным в процессе «обучения» нейронной сети. После выполнения процедуры «обучения» параметры нейронной сети заносятся в блок автонастройки. В соответствии с теорией нейронных сетей «обученная» нейронная сеть должна вести себя так же, как и эксперт, причём даже при тех входных воздействиях, которые не были включены в набор сигналов, использованных при «обучении».
Длительность процесса «обучения» является основной преградой на пути широкого использования методов нейронных сетей в ПИД-регуляторах [16]. Другими недостатками нейронных сетей являются невозможность предсказания погрешности регулирования для воздействий, которые не входили в набор обучающих сигналов, а также отсутствие критериев выбора количества нейронов в сети, длительности «обучения», диапазона и количества обучающих воздействий. Ни в одной из публикаций не исследовалась робастность или запас устойчивости регулятора.
Генетические алгоритмы
Генетические алгоритмы являются мощным методом оптимизации, позволяющим найти глобальный оптимум быстрее, чем другие методы случайного поиска. Существенным их достоинством является отсутствие проблем со сходимостью и устойчивостью. Эти методы используются для идентификации моделей объектов управления, для поиска оптимальных параметров регулятора, для поиска оптимальных положений функций принадлежности в фаззи-регуляторах и для «обучения» нейронных сетей. Чаще всего генетические алгоритмы используются совместно с нейронными сетями и регуляторами с нечёткой логикой.
Недостатком генетических алгоритмов является большое время поиска экстремума, что не позволяет их использовать в быстродействующих системах реального времени.
Генетические алгоритмы основаны на принципах естественного отбора, сформулированных Дарвиным в 1859 году. Идею генетических алгоритмов применительно к решению математических задач сформулировал Дж. Холланд в 1962 году. В генетических алгоритмах используются понятия генов, хромосом, скрещивания, мутация, селекции, репродукции. Основной идеей генетических алгоритмов является прямое подобие принципу естественного отбора, когда выживают наиболее приспособленные особи.
Для применения генетических алгоритмов необходимо преобразовать переменные, фигурирующие в условии задачи, в генетические переменные. Такое преобразование задаётся схемой кодирования. Переменные могут быть представлены в двоичной форме, в форме действительных десятичных чисел или в другой форме, в зависимости от смысла решаемой задачи.
Классический генетический алгоритм состоит из следующих шагов [17].
-
Выбор исходной популяции хромосом размера N.
-
Оценка приспособленности хромосом в популяции.
-
Проверка условия остановки алгоритма.
-
Селекция хромосом.
-
Применение генетических операторов.
-
Формирование новой популяции.
-
Переход к пункту 2.
Для работы алгоритма нужно задать нижнюю и верхнюю границы изменения искомых параметров, вероятность скрещивания, вероятность мутации, размер популяции и максимальное количество поколений.
Исходная популяция хромосом генерируется случайным образом. Приспособленность хромосом оценивается с помощью целевой функции в кодированной форме. Далее хромосомы с лучшей приспособленностью собираются в группу, в пределах которой выполняются генетические операции скрещивания или мутации. Скрещивание позволяет получить от двух родителей перспективного потомка. Оператор мутации вносит изменения в хромосомы. В случае двоичного кодирования мутация состоит в изменении случайного бита в двоичном слове.
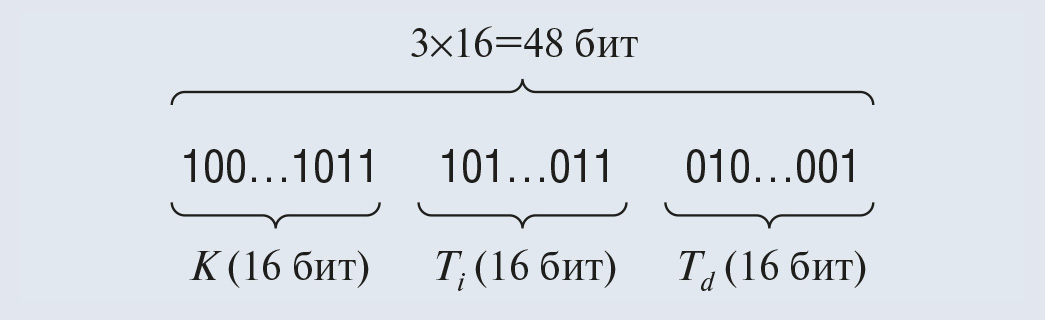
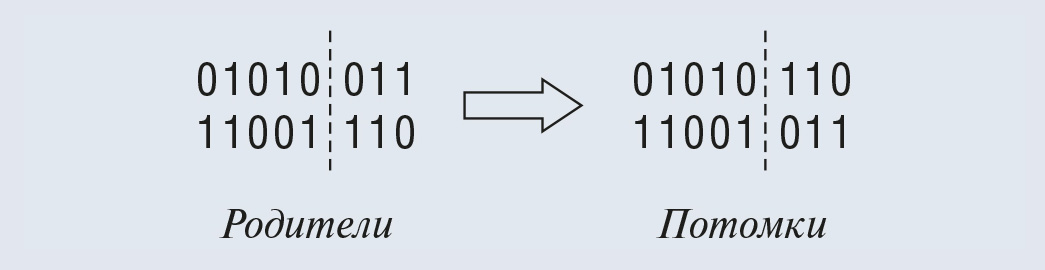
Пример кодирования трёх коэффициентов ПИД-регулятора для применения в генетических алгоритмах приведён на рис. 35 [23]. Здесь хромосома состоит из трёх параметров общей длиной 48 бит. Операция скрещивания состоит в обмене генетическим материалом между хромосомами (родителями) для того, чтобы получить новую хромосому (потомка). Существует много различных форм операторов скрещивания. Один из них состоит в том, что в двух родительских хромосомах случайным образом выбирается некоторая позиция (рис. 36), затем происходит обмен генетической информацией, расположенной справа от выбранной позиции [24]. После выполнения генетического алгоритма производят декодирование генетического представления результата в инженерные величины.
Оценка приспособленности хромосом в популяции для оценки коэффициентов ПИД-регулятора может быть выбрана, к примеру, как
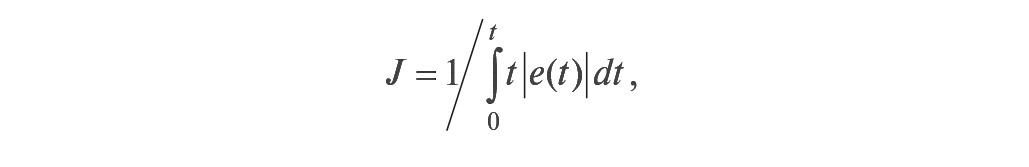
где e(t) – текущее значение ошибки регулирования, t – время [23].
Селекция хромосом осуществляется методом рулетки. На колесе рулетки имеются секторы, причём ширина сектора пропорциональна функции приспособленности. Поэтому чем больше значение этой функции, тем более вероятен отбор соответствующей ей хромосомы.
В работе [25] генетические алгоритмы используются как для идентификации объекта управления, так и для настройки параметров ПИД-регулятора. В обоих случаях схема применения алгоритма одинакова: составляется критериальная функция, зависящая в первом случае от параметров объекта управления, во втором – от параметров ПИД-регулятора K, Td, Ti. Далее с помощью генетического алгоритма отыскивается глобальный минимум функции, координатами которого являются искомые параметры объекта или ПИД-регулятора.
В работе [23] поиск оптимальных параметров ПИД-регулятора выполнялся генетическим алгоритмом со следующими параметрами: размер популяции – 20, максимальное количество поколений – 100, вероятность скрещивания – 0,9, вероятность мутации – 0,1, диапазон изменения параметров 0…40.
Выводы
-
ПИД-регулятор остаётся основным типом регулятора в АСУ ТП.
-
Улучшить характеристики классического ПИД-регулятора может применение регулятора с двумя степенями свободы и фильтра для сигнала уставки.
-
Принцип разомкнутого управления, введённый в ПИД-регулятор, позволяет существенно уменьшить время регулирования и повысить запас устойчивости системы, а также скомпенсировать внешние возмущения.
-
В системах, где время регулирования является определяющим показателем, следует использовать импульсное управление без обратной связи перед включением обычного ПИД-регулятора.
-
Регулятор с точно идентифицированной внутренней моделью позволяет увеличить точность слежения за уставкой, но плохо ослабляет внешние возмущения.
-
Для систем с транспортной задержкой более, чем 0,2…1 от постоянной времени объекта, следует использовать предиктор Смита или ППИ-регулятор.
-
Если объект управления нелинеен, сложен и не может быть идентифицирован, но имеются эвристические правила или опыт ручного управления таким объектом, то решить задачу управления можно с помощью фаззи- или нейросетевого регулятора.
-
Для поиска оптимальных значений параметров ПИД-регуляторов и идентификации объектов управления с успехом используются генетические алгоритмы. ●
Литература
10. Изерман Р. Цифровые системы управления. — М. : Мир, 1984. — 541 с.
11. Smith O.J.M. Close control of loops with dead time // Chemical Engineering Progress. 1957. Vol. 53. P. 217-235.
12. Методы робастного, нейро-нечёткого и адаптивного управления: Учебник / Под ред. Н.Д. Егупова, 2-е изд. — М. : Изд-во МГТУ им. Баумана, 2002. — 744 с.
13. Zadeh L.A. Fuzzy sets // Information and Control. 1965. № 8. P. 338-353.
14. Ротач В.Я. Теория автоматического управления. — М. : Изд-во МЭИ, 2004. — 400 с.
15. Mamdani E.H. Application of fuzzy algorithm for simple dynamic plant // Proc. IEEE. 1974. № 12. P. 1585-1588.
16. Усков А.А., Кузьмин А.В. Интеллектуальные технологии управления. Искусственные нейронные сети и нечёткая логика. — М. : Горячая линия — Телеком, 2004. — 143 с.
17. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечёткие системы. — М. : Горячая линия — Телеком, 2006. — 383 с.
18. Mann G.K.I., Bao-Gang Hu, Gosine R.G. Analysis of direct action fuzzy PID controller structures // IEEE Transactions on Systems, Man and Cybernetics, Part B. June 1999. Vol. 29. Issue 3. P. 371-388.
19. Yesil E., Guzelkaya M., Eksin I. Internal model control based fuzzy gain scheduling technique of PID controllers // World Automation Congress, 28 June - 1 July 2004. Proceedings. Vol. 17. P. 501-506.
20. Feng H.-M. A self-tuning fuzzy control system design // IFSA World Congress and 20th NAFIPS International Conference, 25-28 July 2001. Vol. 1. P. 209-214.
21. Kato M., Yamamoto T., Fujisawa S. A skill-based PID controller using artificial neural networks // Computational Intelligence for Modeling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce, 28-30 Nov. 2005. Vol. 1. P. 702-707.
22. Kawafuku R., Sasaki M., Kato S. Self-tuning PID control of a flexible micro-actuator using neural networks // IEEE International Conference on Systems, Man and Cybernetics, 11-14 Oct. 1998. Vol. 3. P. 3067-3072.
23. Li Jie, Xie Jian-ying, Wu Zheng-mao. Design of disturbance rejection PID controllers for time delay system based on genetic algorithms // International Conference on Neural Networks and Brain (ICNN&B '05), 13-15 Oct. 2005. Vol. 2. P. 876-880.
24. Fleming P.J., Purshouse R.C. Genetic algorithms in control systems engineering. — IFAC Professional Brief. — http://www.ifac-control.org. — 32 p.
25. Pereira D.S., Pinto J.O.P. Genetic algorithm based system identification and PID tuning for optimum adaptive control // IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 2005. Proceedings. P. 801-806.
Автор — сотрудник НИЛ АП
Телефон: (8634) 324-140
Факс: (8634) 324-139
E-mail: info@RLDA.ru
Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!