ПИД-регуляторы: вопросы реализации. Часть 2

Часть 2

Расчёт параметров регулятора

Перед тем как рассчитывать параметры регулятора, необходимо сформулировать цель и критерии качества регулирования, а также ограничения на величины и скорости изменения переменных в системе. Традиционно основные качественные показатели формулируются исходя из требований к форме реакции замкнутой системы на ступенчатое изменение уставки. Однако такой критерий очень ограничен. В частности, он ничего не говорит о величине ослабления шумов измерений или влияния внешних возмущений, может дать ошибочное представление о робастности системы.

Поэтому для полного описания или тестирования системы с ПИД-регулятором нужен ряд дополнительных показателей качества, о которых речь пойдёт дальше.

В общем случае выбор показателей качества не может быть формализован полностью и должен осуществляться, исходя из смысла решаемой задачи.

Качество регулирования

Выбор критерия качества регулирования зависит от цели, для которой используется регулятор. Целью может быть:

• поддержание постоянного значения параметра (например, температуры);

• слежение за изменением уставки или программное управление;

• управление демпфером в резервуаре с жидкостью и т.д.

Для той или иной задачи наиболее важным фактором может быть:

• форма отклика на внешние возмущения (время установления, перерегулирование, время отклика и др.);

• форма отклика на шумы измерений;

• форма отклика на сигнал уставки;

• робастность по отношению к разбросу параметров объекта управления;

• экономия энергии в управляемой системе;

• минимизация шумов измерений.

Для классического ПИД-регулятора параметры, которые являются наилучшими для слежения за уставкой, в общем случае отличаются от параметров, наилучших для ослабления влияния внешних возмущений. Для того чтобы оба параметра одновременно были оптимальными, необходимо использовать ПИД-регуляторы с двумя степенями свободы [1].

Точное слежение за изменением уставки необходимо в системах управления движением, в робототехнике; в системах управления технологическими процессами, где уставка обычно остаётся длительное время без изменений, требуется максимальное ослабление влияния нагрузки (внешних возмущений); в системах управления резервуарами с жидкостью требуется обеспечение ламинарности потока (минимизация дисперсии выходной переменной регулятора) и т.д.

 

Ослабление влияния внешних возмущений

Как было показано в подразделе «Функции чувствительности» (часть 1), обратная связь ослабляет влияние внешних возмущений в |S(jω)| раз за исключением тех частот, на которых |S(jω)|>1. Внешние возмущения могут быть приложены к объекту в самых разных его частях, однако, когда конкретное место неизвестно, считают, что возмущение воздействует на вход объекта. В этом случае отклик системы на внешние возмущения определяется передаточной функцией со входа внешних возмущений на выход системы:

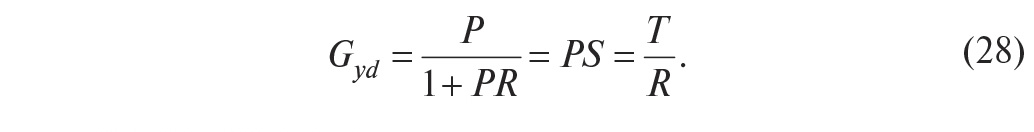
Поскольку внешние возмущения обычно лежат в низкочастотной части спектра, где |S(jω)|<1 и, следовательно, T ≈1, то выражение (28) можно упростить:

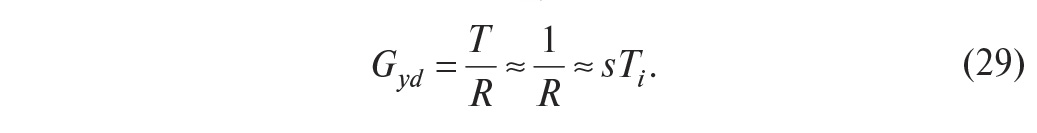
Таким образом, для ослабления влияния внешних возмущений (в частности, влияния нагрузки) можно уменьшить постоянную интегрирований T_i.

Во временной области реакцию на внешние возмущения оценивают по отклику на единичный скачок d(t).

Ослабление влияния шумов измерений

Передаточная функция от точки приложения шума на выход системы имеет вид [1]:

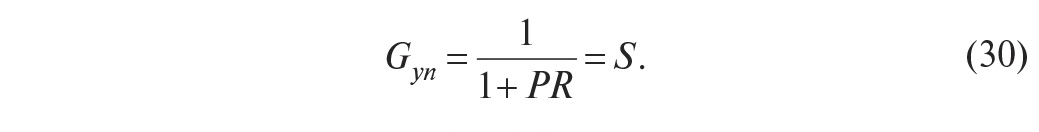
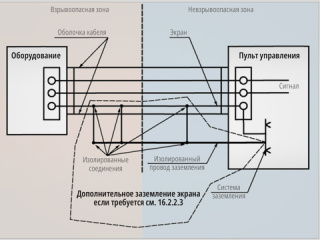
Благодаря спаду АЧХ объекта на высоких частотах функция чувствительности стремится к 1 (рис. 16). Поэтому ослабить влияние шумов измерений с помощью обратной связи невозможно. Однако эти шумы легко устраняются применением фильтров нижних частот, а также правильным экранированием и заземлением [3, 4].

 

Робастность к вариации параметров объекта

Замкнутая система остаётся устойчивой при изменении параметров объекта на величину ∆P(jω), если выполняется условие (18).

Критерии качества во временной области

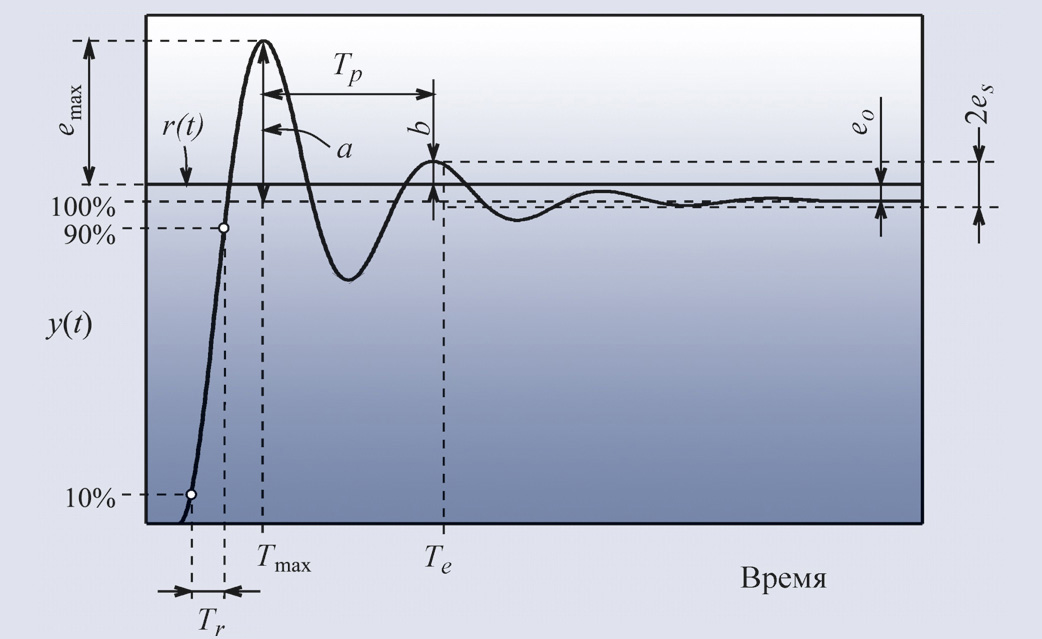
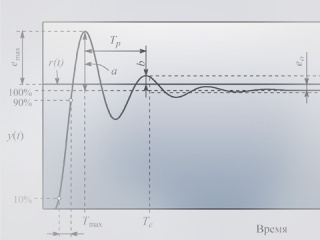
Для оценки качества регулирования в замкнутой системе с ПИД-регулятором обычно используют ступенчатое входное воздействие и ряд критериев для описания формы переходного процесса (рис. 19):

• максимум ошибки регулирования
  
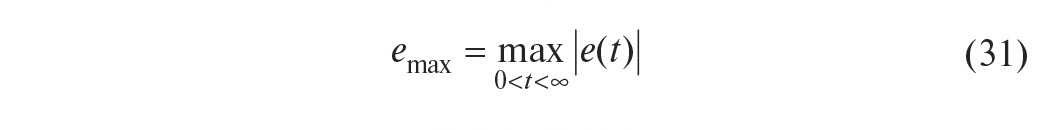
  и момент времени T_max, при котором ошибка достигает этого максимума;

• интегрированная абсолютная ошибка
  
  

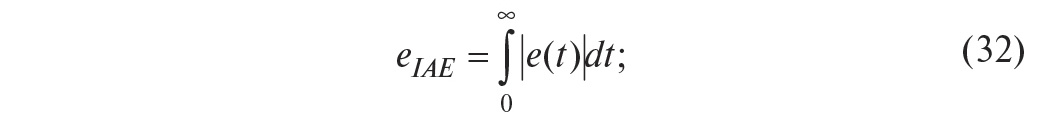
• интеграл от квадрата ошибки
  
  

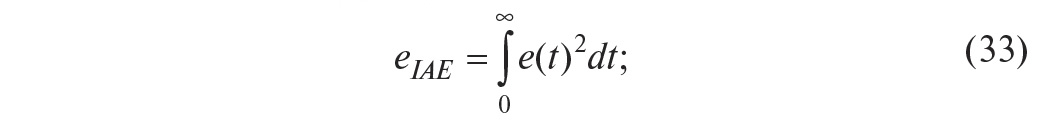
• декремент затухания d (это отношение первого максимума ко второму, типовое значение d=4 и более)
  
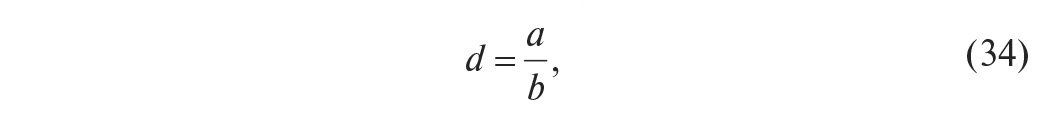
  отметим, что в литературе встречаются и другие определения декремента затухания, в частности, как b/a или как коэффициент в показателе степени экспоненты, описывающей огибающую затухающих колебаний;

• статическая ошибка e_o (это постоянная ошибка в равновесном, то есть в установившемся, или статическом, режиме системы);

• время установления T_e с заданной погрешностью e_s (это время, по истечении которого погрешность регулирования не превышает заданного значения e_s; обычно e_s = 1%, реже 2% или 5% – соответственно время установления обозначают T_0,01, T_0,02, T_0,05);

• перерегулирование e_max (это превышение первого выброса над установившимся значением переменной, обычно выражается в процентах от установившегося значения);

• время нарастания T_r (это интервал времени, в течение которого выходная переменная нарастает от 10 до 90% от своего установившегося значения);

• период затухающих колебаний T_cl (строго говоря, затухающие колебания не являются периодическими, поэтому здесь под периодом понимается расстояние между двумя соседними максимумами переходной характеристики).

Для систем управления движением в качестве тестового сигнала чаще используют не функцию скачка, а линейно нарастающий сигнал, поскольку электромеханические системы обычно имеют ограниченную скорость нарастания выходной величины.

Приведённые критерии используются для оценки качества реакции как на изменение уставки, так и на воздействие внешних возмущений и шумов измерений.

Частотные критерии качества

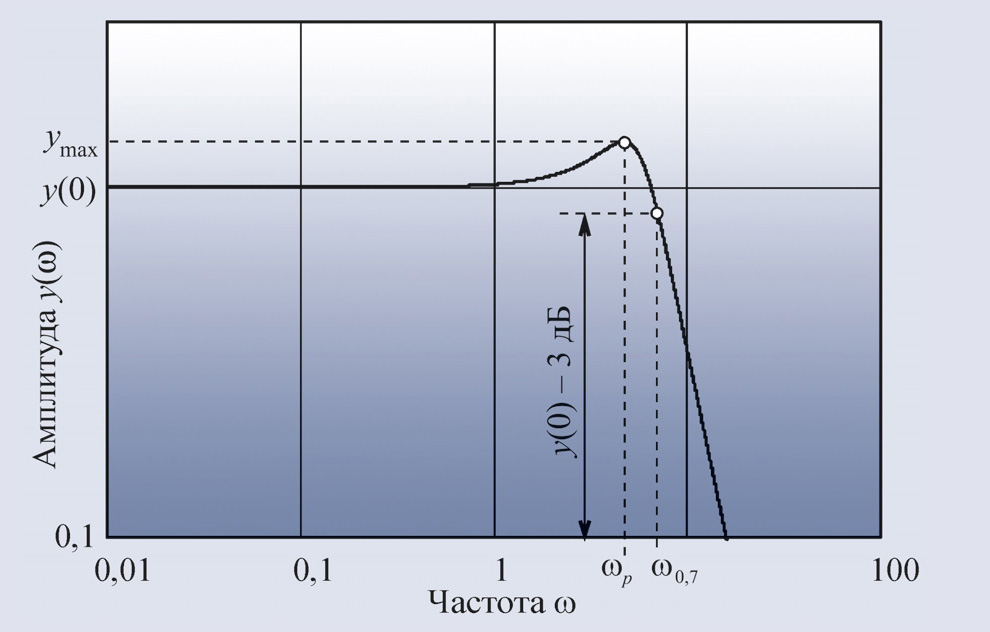
В частотной области обычно используются следующие критерии, получаемые из графика амплитудно-частотной характеристики замкнутой системы y(ω) (рис. 20):

• полоса пропускания ω_–3дБ (или ω_0,7) по уровню –3 дБ (или по уровню 1/√2 = 0,7) – полоса частот от 0 до ω_–3дБ = ω_0,7, в пределах которой кривая АЧХ снижается не более чем на 3 дБ относительно её значения на нулевой частоте y(0);

• колебательность М – отношение максимального (пикового) значения АЧХ y_max к её значению на нулевой частоте y(0), то есть в установившемся режиме
  
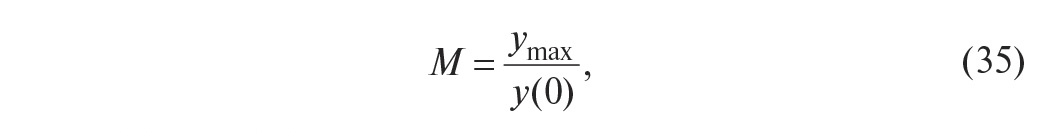
  типовыми значениями являются М = 1,5...1,6;

• резонансная частота системы ω_p – частота, на которой АЧХ достигает максимума y_max = y(ω_p).

Частотные критерии у реальных регуляторов не могут быть однозначно связаны с временными критериями из-за нелинейностей (обычно это нелинейности типа «ограничение») и алгоритмов устранения эффекта интегрального насыщения. Однако приближённо можно установить следующие зависимости между критериями в частотной и временной областях:

• 
  

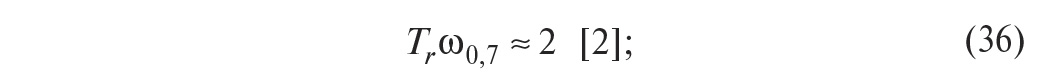
• частота максимума передаточной характеристики замкнутой системы приблизительно соответствует периоду затухающих колебаний отклика на ступенчатое входное воздействие – ω_з ≈ 2π/T_p

• чем медленнее затухают колебания, тем больше показатель колебательности М.

Выбор параметров регулятора

В общей теории автоматического управления структура регулятора выбирается исходя из модели объекта управления. При этом более сложным объектам управления соответствуют более сложные регуляторы. В нашем же случае структура регулятора уже задана – мы рассматриваем ПИД-регулятор. Эта структура очень простая, поэтому ПИД-регулятор не всегда может дать хорошее качество регулирования, хотя в подавляющем большинстве приложений в промышленности применяются именно ПИД-регуляторы.

Впервые методику расчёта параметров ПИД-регуляторов предложили Зиглер и Никольс в 1942 году [8]. Эта методика очень проста и даёт не очень хорошие результаты. Тем не менее она до сих пор часто используется на практике, хотя до настоящего времени появилось множество более точных методов.

После расчёта параметров регулятора обычно требуется его ручная подстройка для улучшения качества регулирования. Для этого используется ряд правил, хорошо обоснованных теоретически.

Для настройки ПИД-регуляторов можно использовать и общие методы теории автоматического управления, такие как метод назначения полюсов и алгебраические методы. В литературе опубликовано и множество других методов, которые имеют преимущества в конкретных применениях. Мы приведём только самые распространённые из них.

Все аналитические (формульные) методы настройки регуляторов основаны на аппроксимации динамики объекта моделью первого или второго порядка с задержкой. Причиной этого является невозможность аналитического решения систем уравнений, которое необходимо при использовании моделей более высокого порядка. В последние годы в связи с появлением мощных контроллеров и персональных компьютеров получили развитие и распространение численные методы оптимизации. Они являются гибким инструментом для оптимальной настройки параметров регулятора для моделей любой сложности и легко учитывают нелинейности объекта управления и требования к робастности.

 

Настройка параметров регулятора по методу Зиглера и Никольса

Зиглер и Никольс предложили два метода настройки ПИД-регуляторов [8]. Один из них основан на параметрах отклика объекта на единичный скачок, второй – на частотных характеристиках объекта управления.

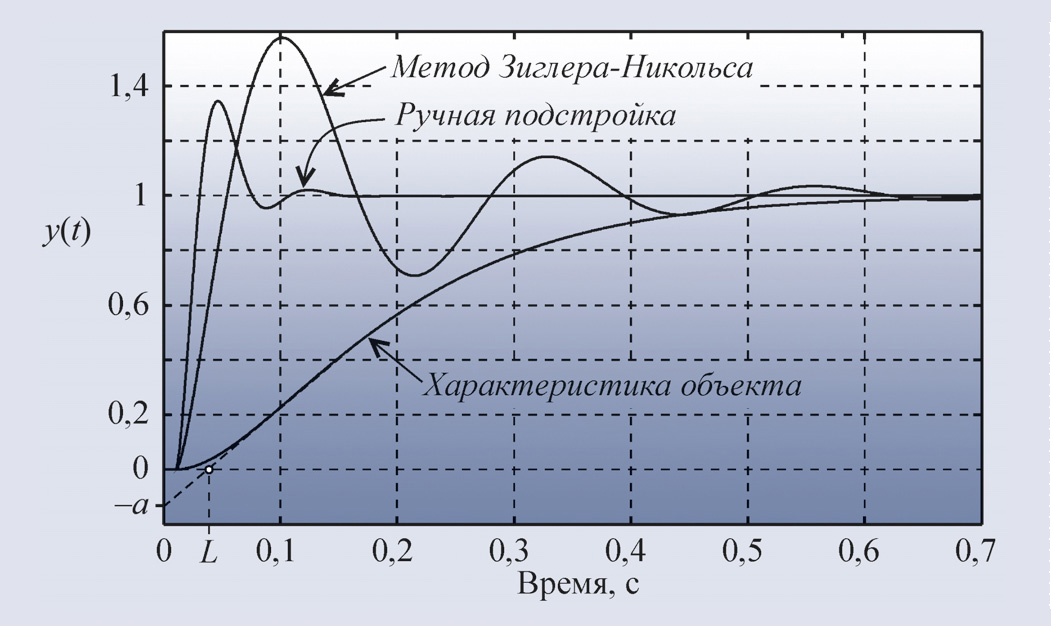
Для расчёта параметров ПИД-регулятора по первому методу Зиглера-Никольса используются всего два параметра: a и L (рис. 21 и пояснения к нему в тексте). Формулы для расчёта коэффициентов ПИД-регулятора сведены в табл. 1.

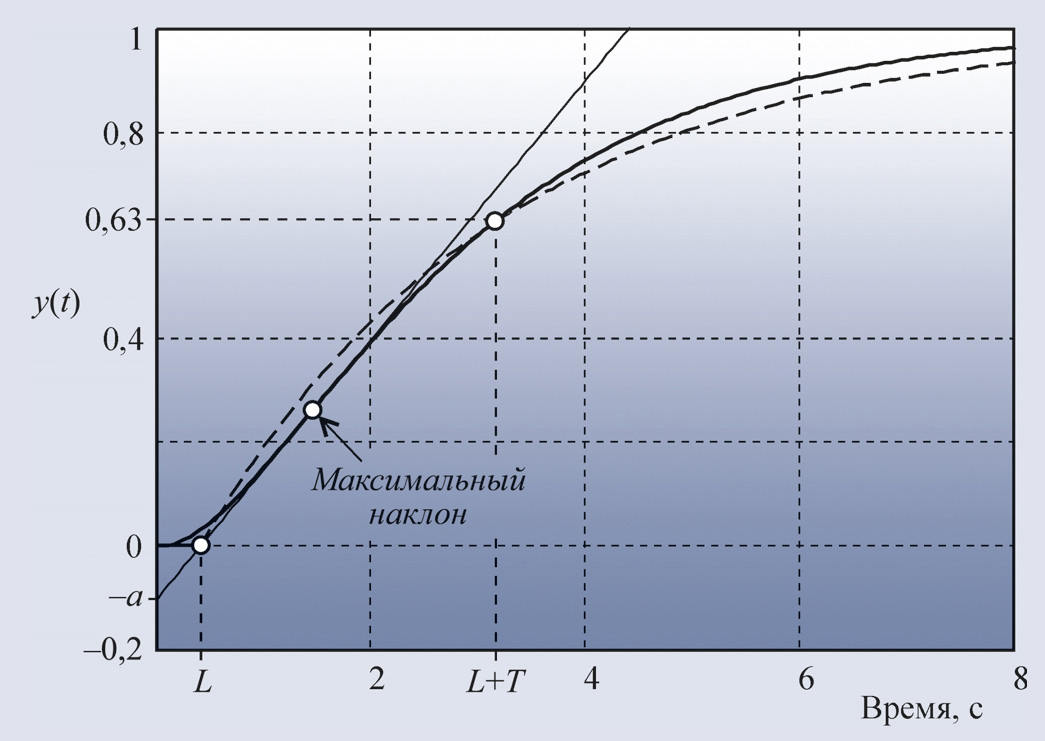
В качестве примера на рис. 22 приведён отклик на единичный скачок системы с объектом второго порядка и ПИД-регулятором, настроенным по табл. 1, и переходная характеристика самого объекта управления. Из характеристики объекта получены значения a = 0,135 и L = 0,135 c. По табл. 1 для этих значений a и L можно найти коэффициенты ПИД-регулятора: K = 8,9, T_i = 0,00796 c, T_d = 0,156 c. 

На рис. 22 приведён также отклик на единичный скачок той же системы при параметрах K =15, T_i = 0,013 c, T_d = 0,525 c, полученных путём ручной подстройки. Как видим, метод Зиглера-Никольса даёт параметры, далёкие от оптимальных. Это объясняется не только упрощённостью самого метода (он использует только 2 параметра для описания объекта), но и тем, что параметры регулятора в этом методе определялись Зиглером и Никольсом, исходя из требования к декременту затухания, равному 4, что и даёт медленное затухание процесса колебаний.

Метод Зиглера-Никольса никак не учитывает требования к запасу устойчивости системы, что является вторым его недостатком. Судя по медленному затуханию переходного процесса в системе, этот метод даёт слишком малый запас устойчивости.

Второй метод Зиглера-Никольса (частотный метод) в качестве исходных данных для расчёта использует частоту ω₁₈₀, на которой сдвиг фаз в разомкнутом контуре достигает 180°, и модуль коэффициента петлевого усиления на этой частоте K₁₈₀. Зная параметр ω₁₈₀, сначала находят период собственных колебаний системы T₁₈₀ = 2π/ω₁₈₀, а затем по табл. 1 определяют параметры регулятора. Точность настройки регулятора и недостатки обоих методов Зиглера-Никольса одинаковы.

 

Метод CHR

В отличие от Зиглера и Никольса, которые использовали в качестве критерия качества настройки декремент затухания, равный 4, Chien, Hrones и Reswick (CHR) [9] использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20-процентного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера-Никольса.

Метод CHR даёт две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки (табл. 2), вторая – при наблюдении отклика на внешние возмущения (табл. 3). 

Какую систему параметров выбирать, зависит от того, что важнее для конкретного регулятора: качество регулирования при изменении уставки или ослабление внешних воздействий. Если же важно и то и другое, то необходимо использовать регуляторы с двумя степенями свободы [1].

Метод CHR использует аппроксимацию объекта моделью первого порядка с задержкой (1).

В CHR используются те же исходные параметры a и L, что и в методе Зиглера-Никольса.

Обратим внимание, что пропорциональный коэффициент в методе CHR меньше, чем в методе Зиглера-Никольса.

Ручная настройка ПИД-регулятора, основанная на правилах

Расчёт параметров по формулам не может дать оптимальной настройки регулятора, поскольку аналитически полученные результаты основываются на сильно упрощённых моделях объекта. В частности, в них не учитывается всегда присутствующая нелинейность типа «ограничение» для управляющего воздействия (см. раздел «Интегральное насыщение»). Кроме того, модели используют параметры, идентифицированные с некоторой погрешностью. Поэтому после расчёта параметров регулятора желательно сделать его подстройку. Подстройку можно выполнить на основе правил, которые используются для ручной настройки. Эти правила получены из опыта, теоретического анализа и численных экспериментов. Они сводятся к следующему [2]:

• увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости;

• с уменьшением интегральной составляющей ошибка регулирования с течением времени уменьшается быстрее;

• уменьшение постоянной интегрирования уменьшает запас устойчивости;

• увеличение дифференциальной составляющей увеличивает запас устойчивости и быстродействие.

Перечисленные правила применяются также для регуляторов, использующих методы экспертных систем и нечёткой логики.

Ручную настройку с помощью правил удобно выполнять с применением интерактивного программного обеспечения на компьютере, временно включённом в контур управления. Для оценки реакции системы на изменение уставки, внешние воздействия или шумы измерений подают искусственные воздействия и наблюдают реакцию на них. После выполнения настройки значения коэффициентов регулятора записывают в память ПИД-контроллера, а компьютер удаляют.

Отметим, что применение правил возможно только после предварительной настройки регулятора по формулам. Попытки настроить регулятор без начального приближённого расчёта коэффициентов могут быть безуспешными.

При регулировке тепловых процессов настройка по правилам может занять недопустимо много времени.

Сформулированные правила справедливы только в окрестности оптимальной настройки регулятора. Вдали от неё эффекты могут быть иными.

Численные методы оптимизации для настройки ПИД-регуляторов

Методы оптимизации для нахождения параметров регулятора концептуально очень просты. Выбирается критерий минимизации, в качестве которого может быть один из показателей качества (см. подразделы «Критерии качества во временной области» и «Частотные критерии качества») или комплексный критерий, составленный из нескольких показателей с разными весовыми коэффициентами. К критерию добавляются ограничения, накладываемые требованиями робастности. Таким путём получается критериальная функция, зависящая от параметров ПИД-регулятора. Далее используются численные методы минимизации критериальной функции с заданными ограничениями, которые и позволяют найти искомые параметры ПИД-регулятора.

Методы, основанные на оптимизации, имеют следующие достоинства:

• позволяют получить оптимальные значения параметров, не требующие дальнейшей подстройки;

• не требуют упрощения модели объекта, модель может быть как угодно сложной;

• позволяют быстро достичь конечного результата (избежать процедуры длительной подстройки параметров).

Однако реализация данного подхода связана с большими проблемами, которые не один десяток лет являются предметом научных исследований. К этим проблемам относятся:

• длительность процесса поиска минимума;

• низкая надёжность метода (во многих случаях вычислительный процесс может расходиться и искомые коэффициенты не будут найдены);

• низкая скорость поиска минимума для овражных функций и функций с несколькими минимумами.

Тем не менее методы оптимизации являются мощным средством настройки ПИД-регуляторов с помощью специально разработанных для этого компьютерных программ (см. раздел «Программные средства для настройки ПИД-регуляторов»).

Автоматическая настройка и адаптация

Естественным направлением развития коммерческих ПИД-регуляторов является разработка методов, позволяющих снизить затраты человеческого труда на инсталляцию, настройку и обслуживание. Несмотря на то что многие методы автоматической настройки и адаптации ПИД-регуляторов, используемые в настоящее время, были разработаны ещё в 60-х годах XX века [10], в промышленных контроллерах адаптивная техника начала использоваться только с середины 80-х. Это связано с технической сложностью реализации адаптивных алгоритмов на элементной базе, которая существовала до появления микроконтроллеров.

Настройка может выполняться вручную или автоматически, без участия человека (автонастройка).

Автонастройка может выполняться полностью автоматически и по требованию, когда человек является инициатором настройки. Полностью автоматическая настройка может инициироваться при наступлении заранее заданного условия (например, при изменении нагрузки, при изменении внешних воздействий, при изменении погрешности регулирования) или непрерывно во времени. Автоматическая настройка, инициируемая без участия человека, называется адаптацией. Примером адаптации может быть автонастройка при изменении числа яиц в инкубаторе или при изменении нагрузки на валу двигателя. Иногда термин «адаптация» трактуют более широко, как приспособление регулятора к реальному объекту на стадии ввода системы в эксплуатацию [10].

Разновидностью адаптации является разомкнутое управление параметрами регулятора (табличная автонастройка), когда заранее найденные параметры регулятора для разных условий работы системы заносятся в таблицу, из которой они извлекаются при наступлении условий, по которым инициируется адаптация.

Отметим, что адаптация в принципе является медленным процессом, поэтому её нельзя рассматривать как непрерывное слежение параметров регулятора за изменяющимися параметрами объекта.

Отметим, что регуляторы, настроенные в автоматическом режиме, чаще настроены хуже, чем настроенные в ручном режиме [11]. Объясняется это философским умозаключением, что компьютер не может выполнять сложные и плохо формализуемые задачи лучше человека.

В настоящий момент отсутствуют простые, надёжные и общепринятые методы автоматической настройки.

Основные принципы

Все виды автоматической настройки используют три принципиально важных этапа: идентификация, расчёт параметров регулятора, настройка регулятора [7]. Часто конечный этап включает этап подстройки (заключительная оптимизация настройки). Оптимизация настройки необходима в связи с тем, что методы расчёта параметров регулятора по формулам не учитывают нелинейности объекта, в частности, всегда присутствующую нелинейность типа «ограничение», а идентификация параметров объекта выполняется с некоторой погрешностью. Подстройка регулятора может быть поисковой (без идентификации объекта, путём поиска оптимальных параметров) и беспоисковой (с идентификацией). Поисковая идентификация базируется обычно на правилах (см. раздел «Ручная настройки ПИД-регулятора, основанная на правилах») или на итерационных алгоритмах поиска минимума критериальной функции. Наиболее распространён поиск оптимальных параметров с помощью градиентного метода: находят производные от критериальной функции по параметрам ПИД-регулятора, которые являются компонентами вектора градиента, а далее производится изменение параметров в соответствии с направлением градиента.

Важно подчеркнуть, что несмотря на наличие автоматической подстройки, контроллер может не дать требуемого качества регулирования по причинам, не зависящим от качества заложенных в него алгоритмов. Например, объект управления может быть плохо спроектирован (зависимые контуры регулирования, большая задержка, высокий порядок объекта); объект может быть нелинейным; датчики могут быть расположены не в том месте, где нужно, и иметь плохой контакт с объектом, уровень помех в канале измерения может быть недопустимо большим; разрешающая способность датчика может быть недостаточно высокой; источник входного воздействия на объект может иметь слишком большую инерционность или гистерезис; могут быть также ошибки в монтаже системы, плохое заземление, обрывы проводников и т.д. Поэтому, прежде чем начинать автоматическую настройку, необходимо убедиться в отсутствии перечисленных проблем. Например, если вследствие износа механической системы появился непредусмотренный проектом гистерезис и поэтому система находится в режиме колебаний, подстройка регулятора может не дать желаемого результата, пока не устранена причина проблемы.

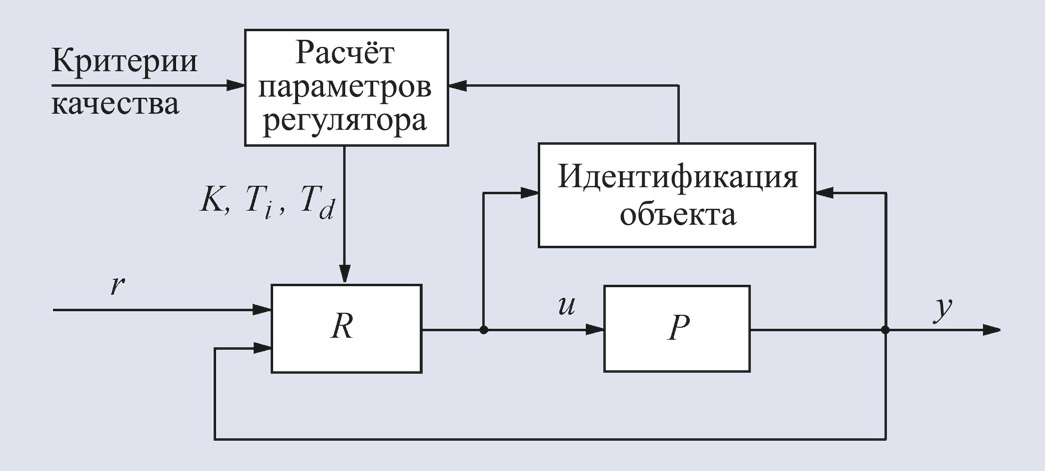
Структурная схема самонастраивающейся системы приведена на рис. 23. Автонастройка практически не имеет никаких особенностей по сравнению с описанными ранее методами, за исключением того, что она выполняется в автоматическом режиме. Основным этапом автоматической настройки и адаптации является идентификация модели объекта. Она выполняется в автоматическом режиме обычными методами идентификации параметров моделей объектов управления [7, 10]. Автоматическая настройка может выполняться и без идентификации объекта, основываясь на правилах (см. раздел «Ручная настройки ПИД-регулятора, основанная на правилах») или поисковых методах.

Идентификация объекта управления

Для выполнения качественного регулирования, в том числе после автоматической настройки ПИД-регулятора, необходимы знания о динамическом поведении объекта управления. Процесс получения (синтеза) математического описания объекта на основе экспериментально полученных сигналов на его входе и выходе называется идентификацией объекта. Математическое описание может быть представлено в табличной форме или в форме уравнений. Идентификация может быть структурной, когда ищется структура математического описания объекта, или параметрической, когда для известной структуры находят величины параметров, входящих в уравнения модели. Когда ищутся параметры модели с известной структурой, то говорят об идентификации параметров модели, а не объекта.

Результатом идентификации может быть импульсная или переходная характеристика объекта, а также соответствующие им спектральные характеристики, которые могут быть представлены в виде таблицы (массива), а не в форме математических зависимостей. Табличные характеристики могут использоваться в дальнейшем для структурной и параметрической идентификации математической модели объекта регулирования или непосредственно для определения параметров ПИД-регулятора (как, например, в методе Зиглера-Никольса, см. подраздел «Настройка параметров регулятора по методу Зиглера и Никольса»).

Несмотря на разнообразие и сложность реальных объектов управления, в ПИД-регуляторах используются, как правило, только две структуры математических моделей: модель первого порядка с задержкой и модель второго порядка с задержкой (см. подраздел «Модели объектов управления»). Гораздо реже используются модели более высоких порядков, хотя они могут более точно соответствовать объекту. Существуют две причины, ограничивающие применение точных моделей. Первой из них является невозможность аналитического решения системы уравнений, описывающих ПИД-регулятор с моделью высокого порядка (а именно аналитические решения получили наибольшее распространение в ПИД-регуляторах с автоматической настройкой). Вторая причина состоит в том, что при большом числе параметров и высоком уровне шума измерений количество информации, полученной в эксперименте, оказывается недостаточным для идентификации тонких особенностей поведения объекта.

Выбор оптимальной модели обычно основан на критерии достаточности качества регулирования при минимальной сложности модели. Для нелинейных процессов и при повышенных требованиях к качеству регулирования разрабатывают модели с индивидуальной структурой, основываясь на физике процессов, протекающих в объекте управления.

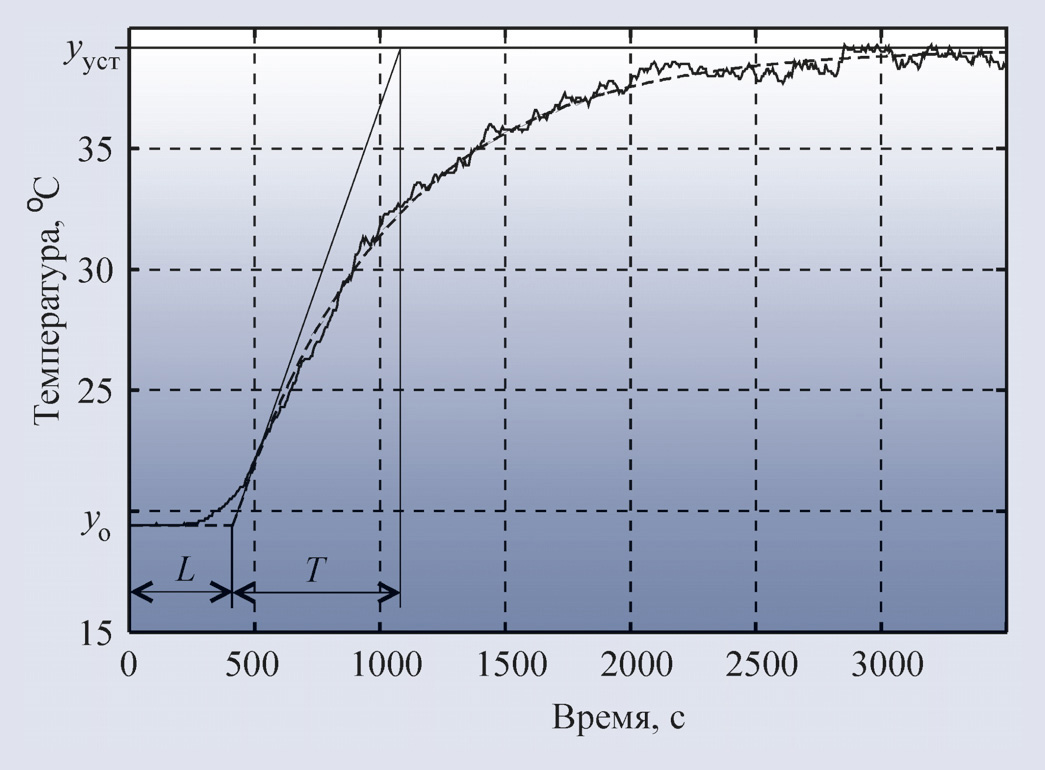
Если процесс любой сложности аппроксимировать моделью первого порядка с транспортной задержкой (рис. 24), то полученные таким способом постоянная времени Т и задержка L называются соответственно эффективной постоянной времени и эффективной задержкой.

Идентификация может выполняться с участием оператора или в автоматическом режиме, а также непрерывно (в реальном времени) – в адаптивных регуляторах либо по требованию оператора – в регуляторах с самонастройкой.

Теория ПИД-регуляторов хорошо развита для линейных объектов управления. Однако практически все реальные объекты имеют нелинейность типа «ограничение управляющего воздействия». Ограничение может быть связано, например, с ограниченной мощностью нагревателя при регулировании тепловых процессов, с ограничением площади сечения перепускного клапана, с ограничением скорости потока жидкости и т.п. Ограничение «снизу» в тепловых системах связано с тем, что источник тепла не может, как правило, работать в режиме холодильника, когда этого требует закон регулирования.

Для минимизации нелинейных эффектов при идентификации объекта в рабочей точке («в малом») используют малые изменения управляющего воздействия, когда нелинейности системы можно не учитывать. При этом процесс вывода системы в зону линейности является предметом отдельного рассмотрения.

Идентификацию можно выполнять в замкнутом контуре с обратной связью или в разомкнутом. Идентификация в замкнутом контуре может быть косвенной и прямой. При косвенной идентификации измеряется тестовый сигнал и отклик на него системы с обратной связью, затем путём вычислений по уравнениям системы находится передаточная функция объекта управления. При прямой идентификации передаточная функция объекта находится по измерениям сигналов непосредственно на его входе и выходе.

Различают активную идентификацию (с помощью воздействия на систему, которое подаётся специально с целью идентификации) и пассивную (в качестве воздействий используют сигналы, имеющиеся в системе в процессе её нормального функционирования). В пассивном эксперименте производят только наблюдение за поведением системы в нормальном режиме её функционирования, пытаясь извлечь из этого наблюдения информацию, достаточную для настройки регулятора.

 

Модели объектов управления

Существуют два способа получения модели объекта управления: формальный и физический. При формальном подходе используют модель типа «чёрный ящик», в которой не содержится информация о физических процессах, происходящих в объекте, или о его структуре. Синтез формальной модели сводится к выбору одной из небольшого числа моделей, описываемых далее, и идентификации её параметров.

Модель первого порядка. Наиболее распространёнными объектами управления являются системы, описываемые уравнениями тепломассопереноса. Реакция таких объектов (при условии, что они являются линейными по входному воздействию) на ступенчатое входное воздействие имеет задержку L и точку перегиба (рис. 24). Точное решение этих уравнений осуществляется численными методами и в теории автоматического управления не используется. Используют достаточно простое выражение передаточной функции объекта управления (модель первого порядка с транспортной задержкой) [6]:

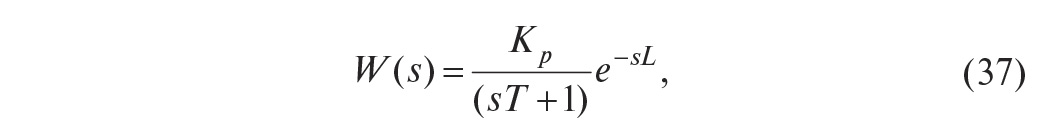
где s – комплексная частота, K_p – коэффициент передачи в установившемся режиме, T – постоянная времени, L – транспортная задержка. Как видим, модель первого порядка описывается тремя параметрами: K_p, T, L, которые должны быть найдены в процессе идентификации. На рис. 24 приведена переходная характеристика реального объекта, измеренная в производственном цехе с помощью модуля NL-4RTD серии RealLab! (НИЛ АП), датчика ТСМ-50, OPC-сервера NLopc и программы MS Excel. Погрешность измерений составляет 1 градус, разрешающая способность – 0,01 градуса. Экспериментально снятые точки (несколько тысяч) образуют сплошную линию, кривая аппроксимирующей модели показана штриховой линией.

Модель второго порядка. Если описанная модель первого порядка оказывается слишком грубой, используют модель второго порядка:

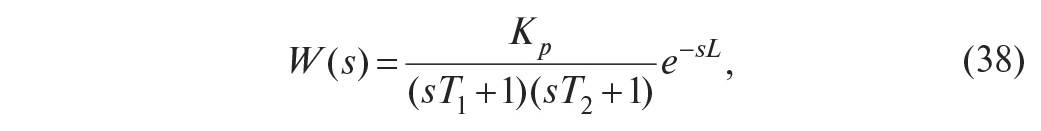
где T₁, T₂ — две постоянные времени объекта управления. Модель второго порядка имеет характерную точку перегиба на передаточной характеристике.

Модели интегрирующих процессов. Выходная величина некоторых объектов управления при подаче на вход ступенчатого воздействия не стремится к установившемуся значению, как на рис. 24, а продолжает изменяться в установившемся режиме. Такие переходные процессы называют интегрирующими. Пример интегрирующего процесса приведён на рис. 25. 

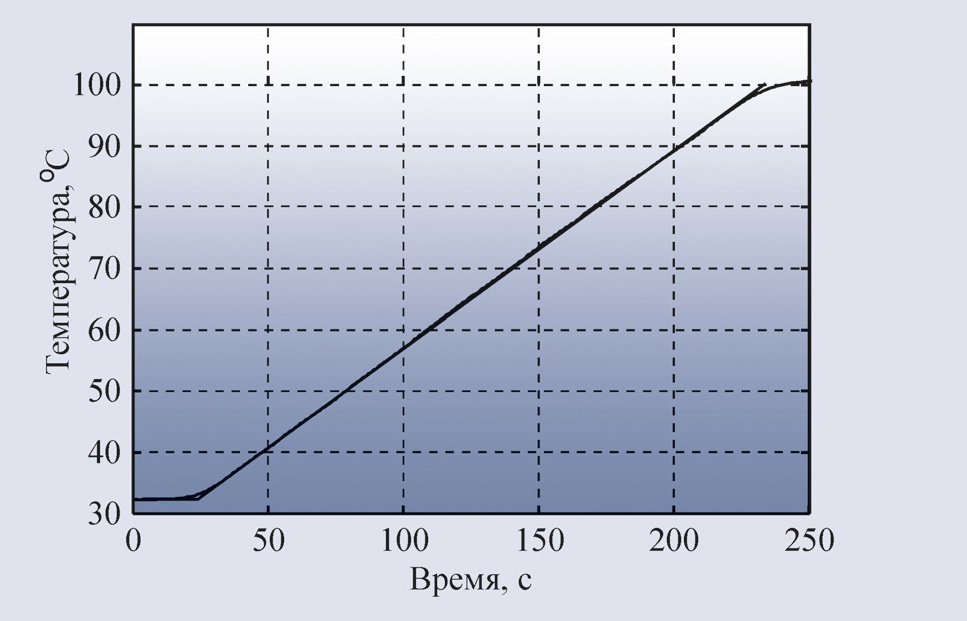
Это зависимость температуры в чайнике мощностью 2 кВт от времени после включения нагрева. Поскольку мощность нагревателя очень высока, то чайник успевает закипеть за время t<<T Передаточная функция такого процесса имеет вид:

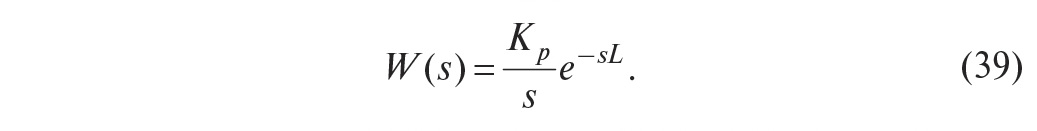
Другими примерами интегрирующих процессов могут быть перемещение ленты транспортёра, поворот оси двигателя, налив жидкости в ёмкость, рост давления в замкнутом сосуде.

Применение более сложных моделей позволяет улучшить качество регулирования, однако делает невозможным простой аналитический расчёт параметров регулятора на основании параметров модели. Для сложных моделей качество регулирования ограничивается не точностью модели, а возможностями ПИД-регулятора. Поэтому наибольшее распространение в ПИД-регуляторах нашли простейшие линейные модели первого и второго порядка.

 

Выбор тестовых сигналов и измерение динамических характеристик

Для идентификации объекта управления необходимо измерять сигнал на его входе u(t) и реакцию y(t) на выходе. Идентификацию можно выполнить не только путём подачи тестового сигнала на вход системы, но и посредством изменения нагрузки (например, нагрузки на валу двигателя), а также параметров объекта (например, количества яиц в инкубаторе).

Идентификация в пассивном эксперименте привлекательна тем, что не вносит погрешность в нормальное течение технологического процесса, однако её достоверность крайне низка в принципе [6] и может привести не к настройке, а расстройке ПИД-регулятора. Тем не менее, число патентов по ПИД-регуляторам с пассивной идентификацией равно числу патентов с активной идентификацией [12].

При проведении активного эксперимента возникает задача выбора формы тестового воздействия. Используют сигналы в форме ступеньки (скачка), в форме прямоугольного импульса, линейно нарастающего сигнала, треугольного импульса, псевдослучайного двоичного сигнала (ПСДС), шума, синусоидальных воздействий (частотный метод). Наиболее часто для настройки ПИД-регуляторов используют скачок и двойной прямоугольный импульс (первый импульс – вверх, второй – вниз относительно установившегося значения).

Тестовое воздействие должно иметь достаточно малую амплитуду, чтобы переходный процесс в объекте оставался в границах линейности. В то же время оно должно быть достаточно большим, чтобы увеличить отношение сигнала к шуму и внешним возмущениям.

Объект должен находиться в установившемся состоянии перед подачей тестового сигнала и быть устойчивым.

Граничная частота спектра тестового сигнала должна быть выше наибольшего по абсолютной величине полюса передаточной функции объекта [10]. Точнее, выше, чем частота единичного усиления ω₁ разомкнутого контура с обратной связью. До настройки регулятора, когда частота ω₁ ещё неизвестна, верхнюю граничную частоту спектра тестового сигнала выбирают выше частоты ω₁₈₀, на которой фазовый сдвиг выходного синусоидального сигнала объекта относительно входного составляет –180°. Указанный диапазон частот важен потому, что именно на частоте ω180 возникают колебания, когда объект находится на границе устойчивости в замкнутом контуре с релейным регулятором или П-регулятором. В контуре с ПИ-регулятором частота затухающих колебаний может быть ниже и соответствовать точке, где сдвиг фаз в объекте составляет около –145° [2] вследствие дополнительного фазового сдвига, вносимого интегратором. В ПИД-регуляторах дифференцирующее звено может скомпенсировать этот фазовый сдвиг, и колебания возникнут на частоте ω₁₈₀.

Нижняя граница диапазона, в котором необходимо достаточно точно идентифицировать передаточную функцию, должна быть примерно в 10 раз ниже частоты единичного усиления ω₁. Более точно нижнюю границу диапазона можно определить только после настройки ПИД-регулятора.

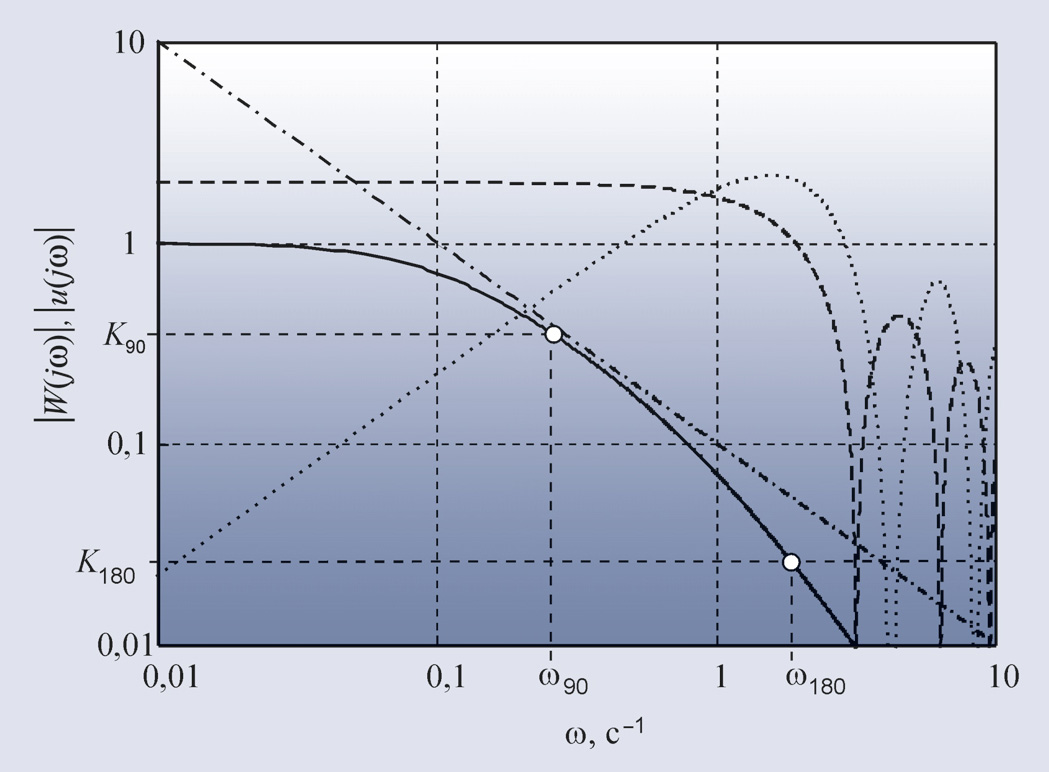
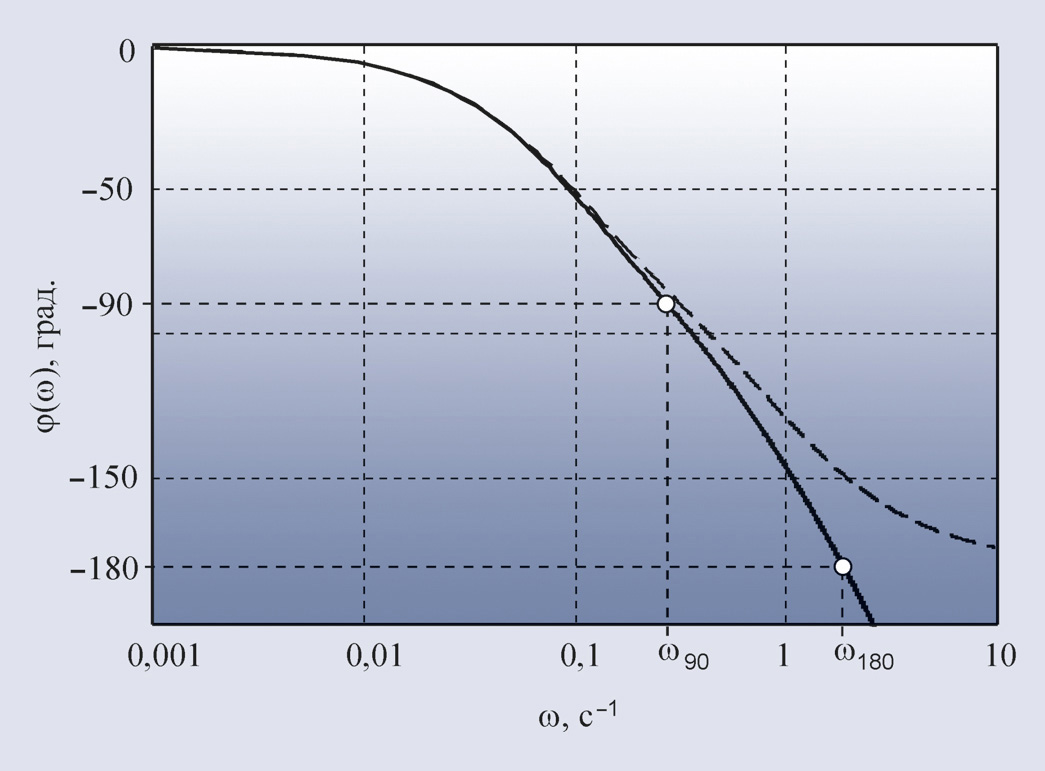
В качестве иллюстрации к сказанному на рис. 26 и рис. 27 сплошной жирной линией показаны амплитудно-частотная и фазочастотная характеристики объекта с передаточной функцией:

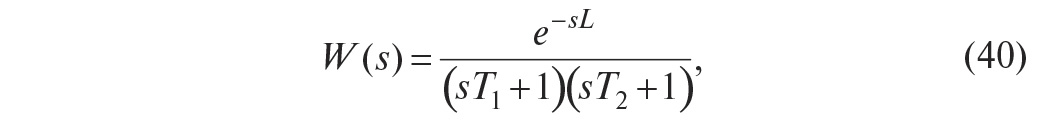
где s = jω, T₁ = 1, T₂ = 10, L = 0,3. Для получения хорошего отношения сигнал/шум зависимость модуля спектральной функции тестового воздействия от частоты не должна иметь сильных провалов в интересующей области частот, чтобы обеспечить достаточно большое отношение сигнал/шум. Этому условию, в частности, удовлетворяют сигналы, показанные штриховой и пунктирной линиями на рис. 26. Желательно также, чтобы порядок функции, описывающей спектральную функцию тестового сигнала (то есть порядок многочлена в знаменателе функции), был не ниже порядка объекта управления, поскольку крутизна спада АЧХ в области верхних частот увеличивается с ростом порядка.

Ширина спектра и мощность тестового сигнала существенно влияют на точность идентификации. В общем случае более мощные и широкополосные сигналы позволяют определить большее число параметров передаточной функции.

Если идентификация выполняется без остановки технологического процесса (а это наиболее важный для практики случай), то могут существовать ограничения на максимальную мощность, длительность или энергию тестового сигнала, чтобы не нарушать нормальный ход технологического процесса. Например, в инкубаторе допускается подать импульс, кратковременно (на 5 минут) повышающий температуру до 50°С, однако повышение температуры даже на 1°С в течение нескольких часов приводит к гибели зародыша. Поэтому возникает задача выбора тестового сигнала с требуемым спектром при ограничении, накладываемом на его мощность, длительность или энергию.

Наилучшую спектральную характеристику можно получить, усложняя форму сигнала и увеличивая общее время идентификации. Для идентификации быстрых процессов (например, в электромеханических системах) получил широкое распространение псевдослучайный двоичный сигнал, имеющий равномерный спектр в ограниченной полосе частот. Однако при управлении тепловыми процессами для ПИД-регуляторов наиболее критическим параметром является быстрота идентификации. Поэтому здесь чаще используют простые сигналы, которые, кроме быстроты идентификации, позволяют использовать простые расчёты по формулам вместо численных методов минимизации функционала ошибки. Конечно, достоверность результата при этом падает.

Даже тщательно выполненная идентификация может не дать положительного результата, если окажется, что объект существенно нелинеен. Для тестирования на линейность объект возбуждают серией тестовых воздействий разной амплитуды. Полученные реакции объекта нормируют на амплитуду тестового сигнала и сравнивают между собой. Для линейных объектов полученные кривые должны совпадать. Если различие между кривыми существенно превышает оценку погрешности идентификации, то объект следует рассматривать как нелинейный и использовать для него методы теории автоматического управления нелинейными системами.

 

Частотная идентификация в режиме релейного регулирования

Идентификация с помощью широкополосных сигналов, к которым относятся единичный скачок и прямоугольный импульс, не позволяет получить достаточно достоверные результаты в условиях сильных шумов и жёстких ограничений, накладываемых на энергию сигнала. Гораздо более высокую точность при малой амплитуде позволяет получить воздействие узкополосным сигналом, в качестве которого используют отрезок синусоидального сигнала. С ростом числа периодов сужается ширина спектра и растёт спектральная плотность такого сигнала на частоте колебаний. Благодаря этому появляется возможность использовать узкополосный фильтр для выделения сигнала на фоне помех, что резко повышает достоверность идентификации. Однако при использовании фильтра перед измерением необходимо дождаться окончания переходного процесса, который тем длиннее, чем выше добротность фильтра. Это существенно увеличивает время идентификации. Идентификацию выполняют для нескольких разных частот. Для ускорения процесса можно использовать тестовое воздействие в виде суммы гармонических колебаний с разными частотами, которые затем выделяют несколькими узкополосными фильтрами.

Существенным недостатком этого метода является большое время идентификации. Поэтому его чаще используют только для измерения коэффициента передачи и фазового сдвига на частоте ω₁₈₀, а для идентификации других параметров объекта используют широкополосные тестовые сигналы.

Метод частотной (релейной) идентификации в замкнутом контуре с релейным регулятором является самым распространённым в коммерческих ПИД-регуляторах с автонастройкой [2, 13]. Этот метод очень давно известен в микроэлектронике как метод кольцевого генератора. Он использует свойство замкнутой динамической системы с отрицательной обратной связью генерировать незатухающие колебания на частоте фазового сдвига –180° при петлевом усилении K₁₈₀ ≥1.

Основная идея метода. Рассмотрим систему с отрицательной обратной связью, состоящую из релейного регулятора R и объекта управления P (рис. 28). 

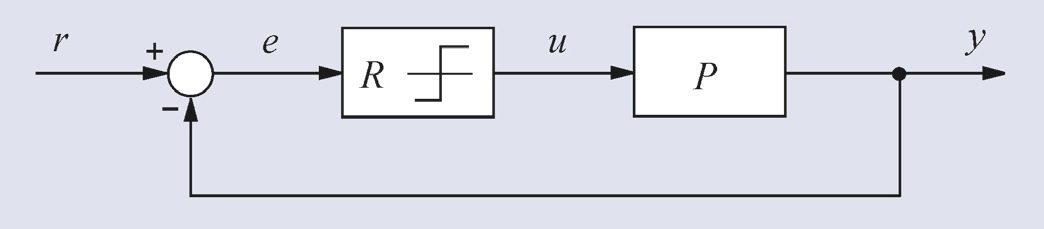
Здесь регулятор R имеет два значения выходной величины u:

Гармонический сигнал, проходя через объект управления, изменяет свою амплитуду и фазу (рис. 26 и 27). Поскольку на входе объекта присутствует шум, в его спектре всегда найдутся такие гармонические составляющие с частотой ω₁₈₀, которые, пройдя через объект управления, появятся на его выходе с той же частотой ω₁₈₀, но с отставанием по фазе на 180° от соответствующей входной составляющей. Если этот сигнал с выхода объекта опять подать на его вход с помощью отрицательной обратной связи, то общий фазовый сдвиг в петле с обратной связью составит уже 360°, то есть на частоте ω₁₈₀ обратная связь в системе из отрицательной превращается в положительную. Это приводит к нарастанию циркулирующего по петле сигнала при петлевом усилении K_n > 1 или к его затуханию при K_n < 1. Нарастание сигнала в некоторый момент начинает ограничиваться, например, нелинейностью типа «насыщение», и тогда в системе устанавливаются стационарные колебания. При этом эффективный коэффициент усиления, найденный по первой гармонике колебаний на частоте ω180, становится равным единице K_n = 1 (так как после установления стационарных колебаний сигнал больше не усиливается).

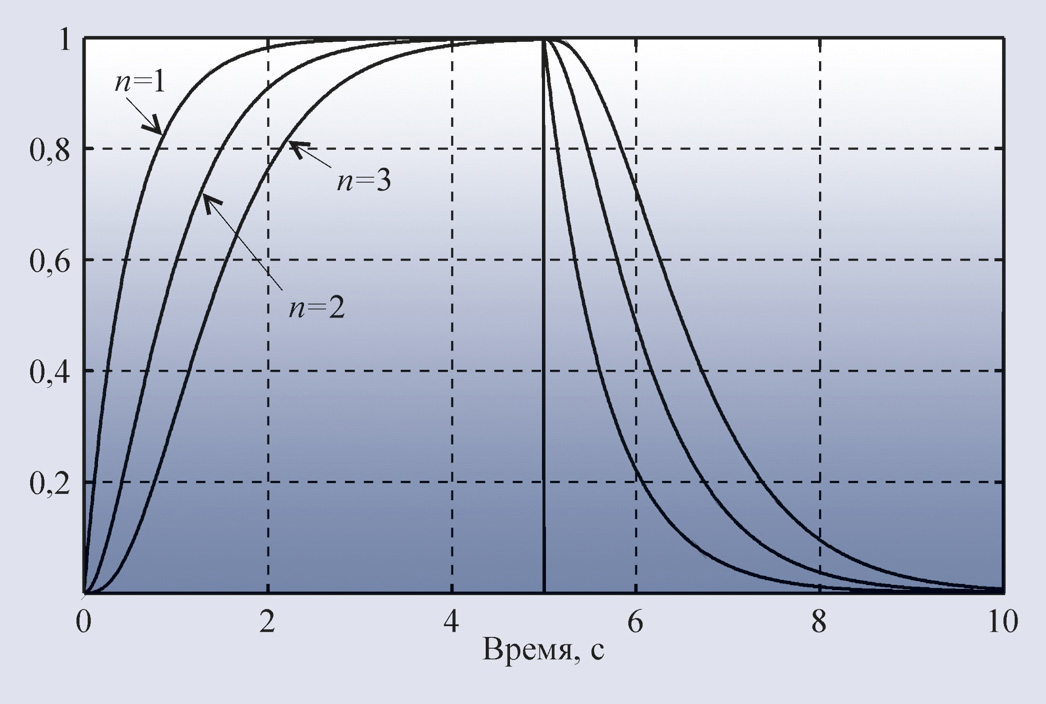
Таким образом, в рассмотренной системе возникают незатухающие колебания, когда усиление по контуру с обратной связью (петлевое усиление) равно единице на частоте фазового сдвига в объекте 180°. В нелинейной системе петлевое усиление на малом сигнале может быть больше единицы до момента, когда колебания установятся. В контуре регулирования с идеальным релейным регулятором (рис. 28) усиление до начала колебаний равно бесконечности. Поэтому, если фазочастотная характеристика включает в себя точку со сдвигом фазы 180°, возникают колебания. С увеличением порядка объекта (рис. 29) сдвиг по фазе становится более 180° и условия для возникновения колебаний выполняются всегда.

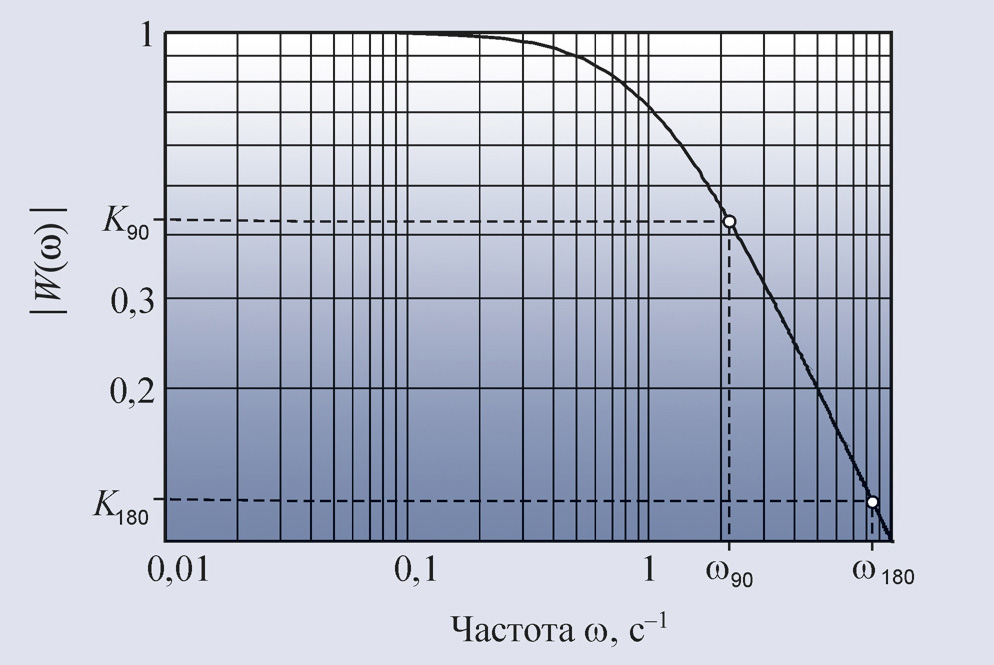
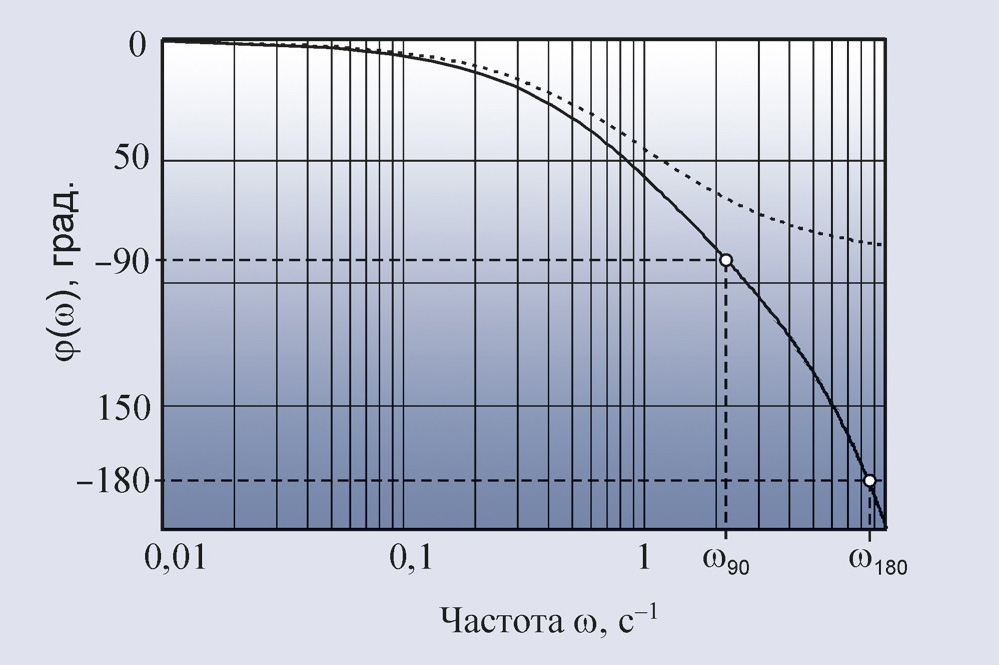
Обычно АЧХ строят в логарифмическом масштабе по обеим координатным осям и называют диаграммами Боде. При этом наклон линейных участков АЧХ измеряют в децибелах на декаду (дБ/дек.). Например, объект первого порядка (1) имеет наклон АЧХ –20 дБ/дек. (рис. 30), и при L = 0 этому наклону взаимно однозначно соответствует максимальный фазовый сдвиг –90° при ω → ∞ (рис. 31, пунктирная линия). Объект второго порядка (2) имеет наклон АЧХ –40 дБ/дек., и ему соответствует максимальный фазовый сдвиг –180° при ω → ∞ (рис. 26). Для объекта третьего порядка наклон АЧХ равен –60 дБ/дек., и фазовый сдвиг составляет –270°.

Из изложенного следует, что система регулирования с объектом первого порядка без транспортной задержки всегда устойчива, даже в контуре с релейным регулятором. Система с объектом второго порядка может быть неустойчивой при ω → ∞. Система с объектом третьего порядка и система любого порядка с транспортной задержкой в контуре с релейным регулятором всегда находится в режиме автоколебаний.

Поэтому качество системы управления в первую очередь нужно обеспечивать путём проектирования объекта управления с минимальным порядком (если это возможно), и только после этого проектировать регулятор для него. Например, некоторые системы термостатирования используют нагревательный элемент в виде тонкой проволочки, через которую продувается воздух. Такая система имеет первый порядок передаточной функции, и даже релейный регулятор для неё даёт хорошее качество регулирования.

Система с объектом первого порядка перестаёт быть устойчивой, если в передаточную функцию добавляется транспортная задержка. При этом объект перестаёт быть минимально-фазовым и, несмотря на то что наклон АЧХ остаётся равным –20 дБ/дек. (рис. 30), в системе возникают колебания, поскольку фазовый сдвиг транспортной задержки ϕ = Lω растёт неограниченно с ростом частоты ω и на частоте ω₁₈₀ достигает –180° (рис. 31, сплошная линия).

Поскольку в реальном объекте вследствие его пространственной протяжённости всегда появляется небольшая транспортная задержка, в любой системе с релейным регулятором возникают колебания, однако их амплитуда на выходе объекта может быть пренебрежимо малой вследствие резкого снижения коэффициента передачи объекта с ростом частоты (рис. 30).

Таким образом, замкнутый контур с объектом управления и релейным регулятором позволяет найти частоту ω₁₈₀. Найдём теперь коэффициент передачи объекта на этой частоте. К сожалению, его можно найти только приближённо, поскольку на вход объекта в системе с релейным регулятором воздействует последовательность прямоугольных импульсов, которая получается после прохождения сигнала обратной связи y(t) через релейный регулятор. Приближённый метод расчёта основан на разложении входной последовательности прямоугольных импульсов в ряд Фурье с отбрасыванием всех гармоник, кроме первой. Возможность замены последовательности прямоугольных импульсов их первой гармоникой основана на том, что объекты с передаточными функциями вида (2) являются фильтрами, ослабляющими высшие гармоники. Серия прямоугольных импульсов, пройдя через такой объект, становится очень близкой к синусоидальному сигналу (рис. 32). Поэтому после разложения входного сигнала в ряд Фурье можно считать, что через объект проходит только первая гармоника, а остальные подавляются.

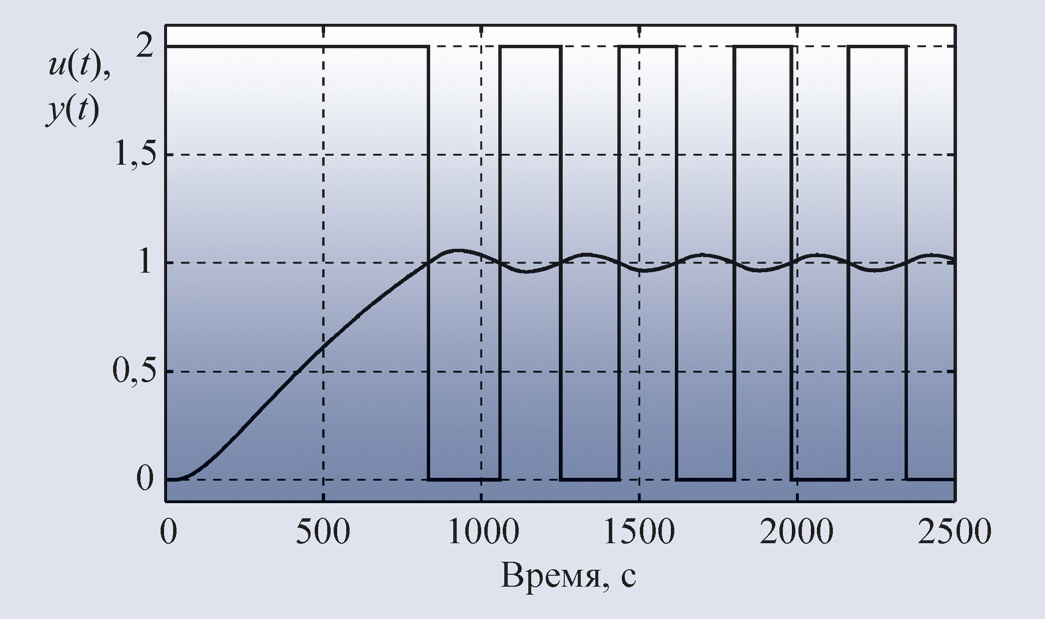
Если размах прямоугольных импульсов на входе объекта равен 2U_max, то амплитуда первой гармоники этих импульсов, как известно из курса радиотехники, равна 4U_max/π. Если обозначить амплитуду первой гармоники сигнала на выходе объекта через Y_max, то искомый коэффициент передачи системы на частоте ω₁₈₀ будет равен отношению амплитуды на выходе к амплитуде на входе:

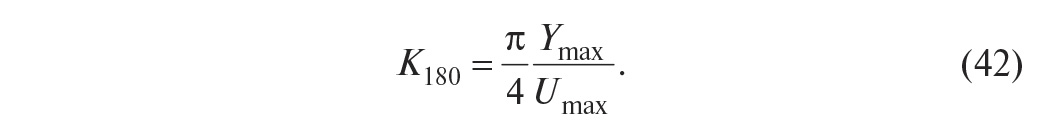
Пример. Рассмотрим АЧХ (рис. 26) и ФЧХ (рис. 27) объекта второго порядка вида (40). Из графика на рис. 27 можно найти частоту ω₁₈₀ = 1,84, а по рис. 26 – коэффициент передачи объекта на этой частоте K₁₈₀ = 0,026. То есть при включении такого объекта в контур с релейным регулятором получим колебания с частотой ω₁₈₀ = 1,84 при усилении K₁₈₀ = 0,026.

Примерно эти же значения можно получить из эксперимента с релейным регулятором по формуле (42), если из графиков на рис. 32 найти значения амплитуды на выходе Y_max = 0,035 и входе U_max = 1, а затем по формуле (42) рассчитать значение K₁₈₀ = 0,027. Значение частоты ω₁₈₀ = 1,8 можно найти непосредственно по графику на рис. 32. Таким образом, приближённая формула в данном случае даёт достаточно низкую погрешность (около 4%).

Для объекта первого порядка с транспортной задержкой L = 0,2 и постоянной времени T = 1 (ω = 2π/Τ) из рис. 31 можно найти ω₁₈₀ = 8,44, а из рис. 30 определить K₁₈₀ = 0,118. Форма колебаний в системе с релейным регулятором показана на рис. 33 (штриховая линия). 

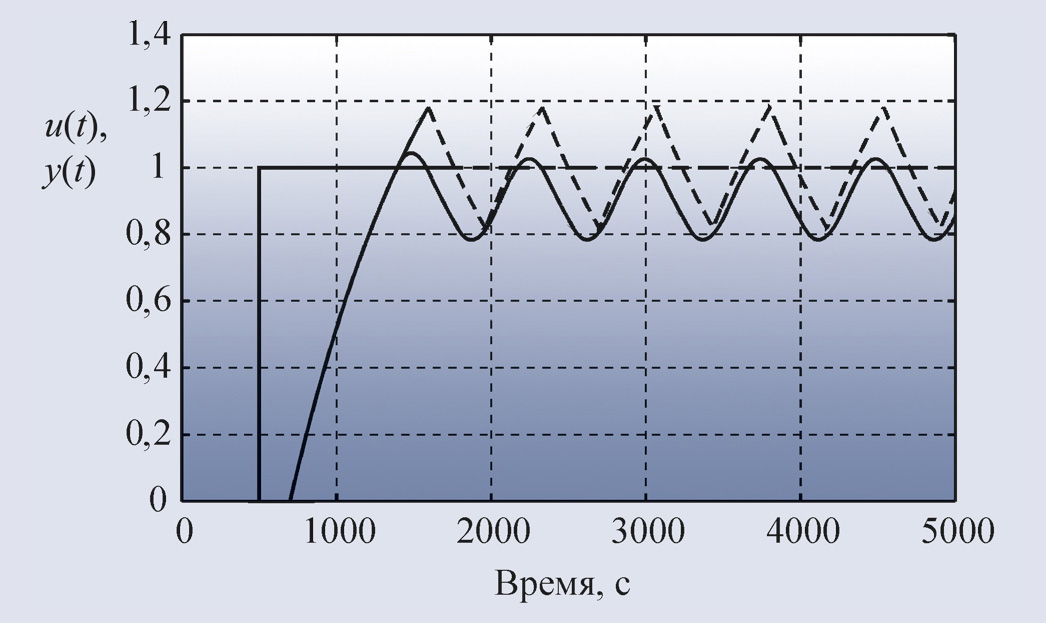
Особенностью объекта первого порядка является существенное отличие формы колебаний от синусоидальной, что делает слишком грубым её аппроксимацию первой гармоникой ряда Фурье, которая была использована при получении формулы (42). Для устранения этой проблемы вместо релейного регулятора можно использовать линейный усилитель, чтобы не искажать форму сигнала в системе. Тогда форма колебаний становится близкой к синусоидальной (сплошная линия на рис. 33). Такая колебательная система даёт довольно точные значения ω₁₈₀ = 8,49 и K₁₈₀ = 0,096. Однако для обеспечения режима, близкого к линейному, петлевое усиление должно быть равно 1, то есть усилитель должен обеспечить усиление в 1/K₁₈₀ раз, где параметр K₁₈₀ априори неизвестен. Это является основным недостатком метода колебаний в линейном режиме.

Важным условием, которое нужно соблюдать при использовании идентификации в режиме релейного регулирования, является симметричность уровней u_max и u_min относительно уровня сигнала u_r, при котором y = r, то есть должно выполняться условие:

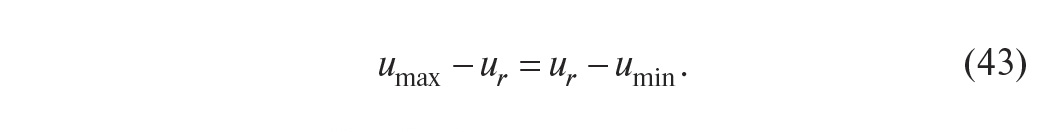
В противном случае скорости нарастания сигнала выше уставки и спада ниже неё будут сильно различаться, а форма колебаний в системе будет существенно отличаться от синусоидальной (рис. 34), что приведёт к высокой погрешности данного метода.

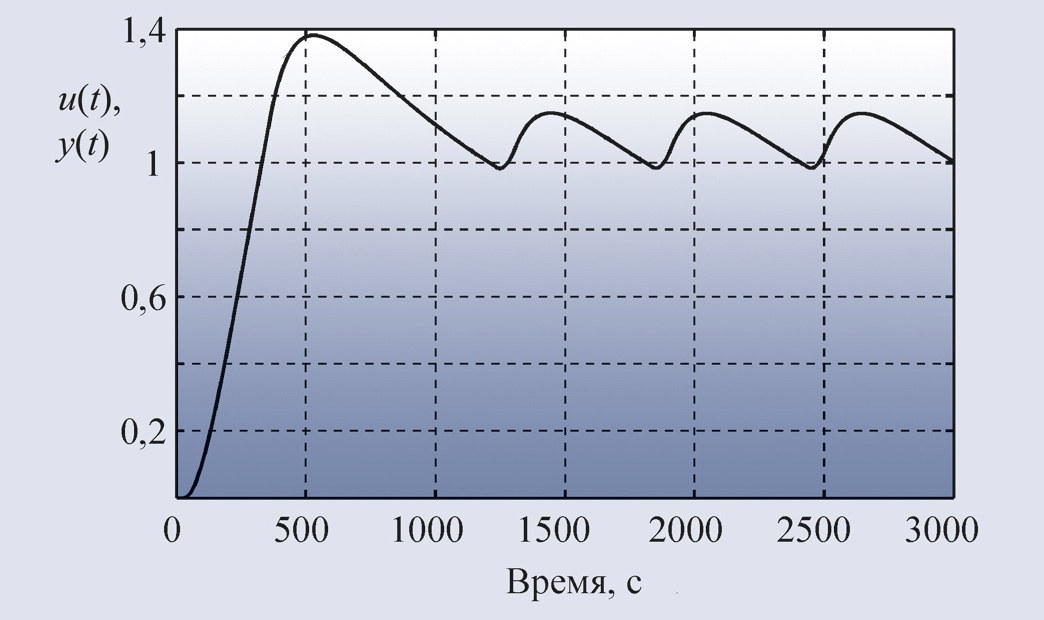
Аналогичный эффект возникает и в системах более высокого порядка, если транспортная задержка превышает наибольшую постоянную времени. С ростом задержки колебания становятся сначала треугольными, затем приближаются к трапецеидальным и прямоугольным. Это объясняется тем, что с ростом транспортной задержки реакция объекта на каждый из фронтов сигнала на выходе реле приближается к форме реакции на функцию единичного скачка (рис. 29). В частотной области указанный эффект объясняется тем, что с ростом задержки точка ω₁₈₀ (рис. 30 и 31) смещается влево, то есть фильтрующие свойства объекта ухудшаются, и он транслирует прямоугольный входной сигнал на свой выход с меньшими искажениями.

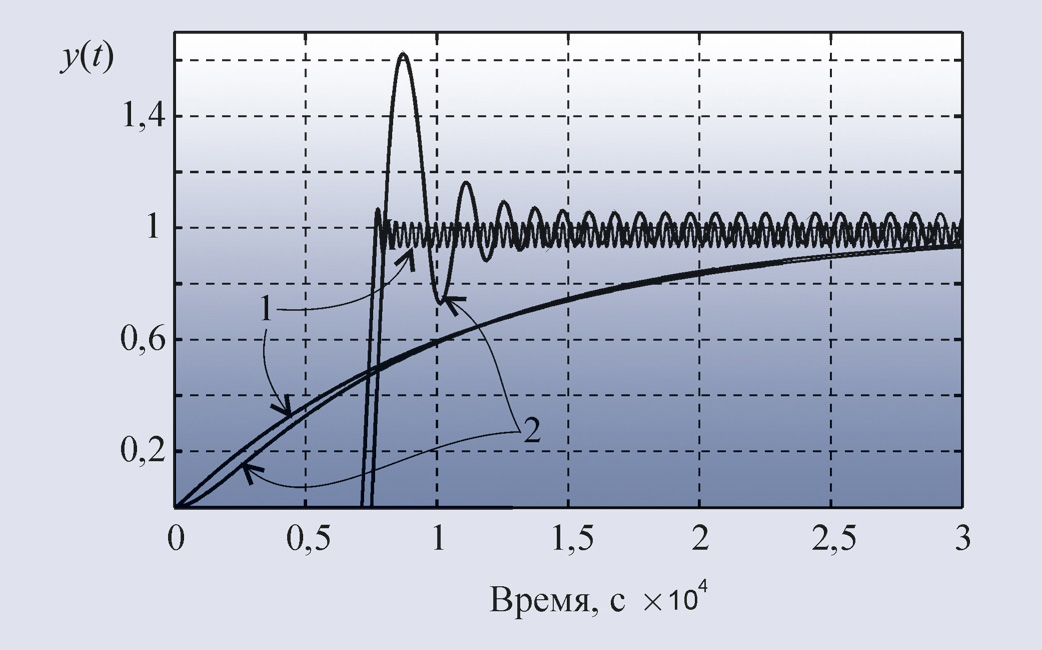
Для иллюстрации высокой разрешающей способности описанного метода на рис. 35 приведены процессы в двух моделях, у которых переходные характеристики различаются слабо, однако частоты колебаний в контуре с релейным регулятором отличаются в 4 раза. Благодаря узкой полосе сигнала он может быть эффективно выделен на фоне шумов, например, методом наименьших квадратов.

Описанный метод позволяет получить только одну точку передаточной функции объекта, то есть два параметра, которых недостаточно для нахождения трёх параметров ПИД-регулятора. Поэтому используют дополнительное соотношение T_i = 4T_d/K² которое позволяет найти третий параметр. 

Чтобы получить и другие точки АЧХ, можно использовать реле с гистерезисом или фильтры, сдвигающие точку ω₁₈₀ в сторону более низких частот.

Описанный метод релейной идентификации является в настоящее время самым распространённым в ПИД-регуляторах с автоматической настройкой. Это объясняется следующими достоинствами метода:

• всегда даёт результат;

• имеет высокую разрешающую способность;

• не требует сложных вычислений;

• даёт результат в рабочей точке.

Метод обладает следующими недостатками:

• не справедлив для большой задержки, когда метод расчёта коэффициента передачи даёт большую ошибку;

• самостоятельно может использоваться только для очень грубой настройки, в общем случае должен комбинироваться с другими методами идентификации.

Табличное управление

Наиболее простым методом адаптации ПИД-регулятора к изменяющимся свойствам объекта управления является табличное управление коэффициентами регулятора. Он может быть использован не только для адаптивного управления, но и для управления нелинейными объектами, нестационарными процессами, при необходимости изменять параметры в зависимости от некоторых условий.

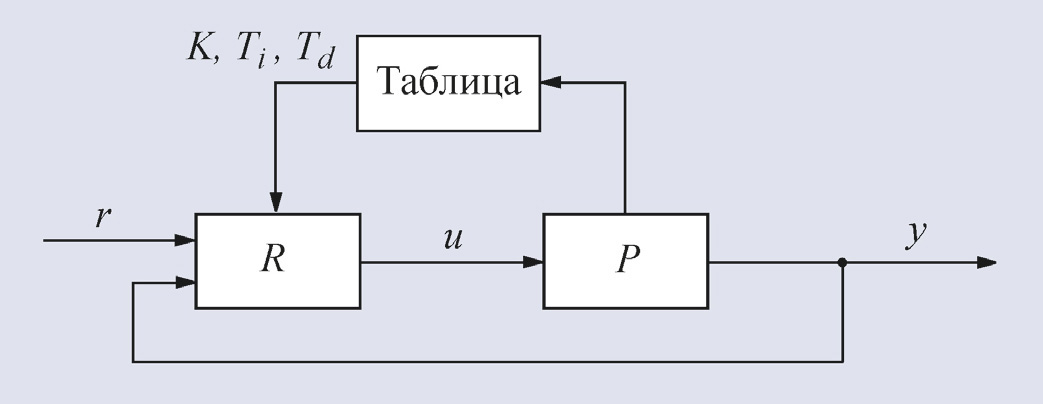
Принцип табличного управления очень прост (рис. 36). Зная заранее возможные изменения режима работы системы (например, возможные варианты загрузки инкубатора яйцами), выполняют идентификацию объекта для нескольких разных режимов и для каждого из них находят параметры регулятора. Значения этих параметров записывают в таблицу. В процессе функционирования системы измеряют величину, которая характеризует режим работы системы (например, вес яиц с помощью датчика веса или уровень жидкости в автоклаве с помощью датчика уровня), и в зависимости от её значений выбирают из таблицы значения коэффициентов ПИД-регулятора.

Описанную систему можно рассматривать как систему с двумя контурами регулирования. Однако контур, служащий для адаптации (в нашем примере с весом яиц в инкубаторе или уровнем жидкости в автоклаве), является разомкнутым. По этой причине табличное управление характеризуется высоким быстродействием, отсутствием ложного срабатывания или расхождения алгоритмов адаптации.

В общем случае таблица может быть многомерной; для снижения необходимой размерности таблицы можно использовать интерполяцию данных с помощью сплайна.

Недостатком этого метода являются большие затраты на предварительную идентификацию, необходимую для составления таблицы. Однако эту проблему частично можно решить посредством применения специальных программ для автоматической идентификации и адаптации регулятора, после выполнения которых полученные параметры заносятся в таблицу.

Табличное управление коэффициентами регулятора целесообразно использовать в тех случаях, когда заранее известны виды и величины дестабилизирующих факторов, которые к тому же можно измерить.

Программные средства для на стройки ПИД-регуляторов

Типовая система для настройки ПИД-регуляторов состоит из компьютера с программным обеспечением под Windows, комплекта модулей ввода-вывода и соединительных кабелей. Объект включается в контур регулирования, система настраивается желаемым способом, затем полученные коэффициенты регулятора записываются в ПИД-контроллер. Благодаря удобному пользовательскому интерфейсу, большой производительности компьютера и отсутствию ограничений на алгоритмы идентификации системы удаётся получить параметры регулятора, близкие к оптимальным.

В настоящее время имеется около полусотни коммерческих продуктов [12] для настройки ПИД-регуляторов.

Среди аналитических методов настройки в этих программах наиболее распространены Lambda-тьюнинг [2] или метод регулятора с внутренней моделью [1]. Подавляющее большинство программ использует модель первого порядка с задержкой для описания объекта регулирования.

Связь с оборудованием выполняется с применением OPC-сервера, DDE-, COM- или DCOM- технологий, среди которых только OPC-сервер является средством, основанным на международном стандарте.

Развитие описываемых средств идёт в направлении расширения диапазона поддерживаемых ПИД-регуляторов, применения методов искусственного интеллекта и методов диагностики, развития пользовательского интерфейса. Современные средства настройки позволяют анализировать износ клапанов, делать оценку робастности, автоматически генерировать отчёт с параметрами контура регулирования, строить графики спектральной плотности мощности и функций авто- и взаимной корреляции, делать оптимизацию инверсной модели объекта управления и т.п.

В качестве примера рассмотрим один из коммерческих продуктов – систему для настройки ПИД-регуляторов Protuner (см. Application manual на сайте www.protuner.com) фирмы Techmation Inc. Система отображает графики переходного процесса, выполняет преобразование экспериментальных характеристик из временной области в частотную и вычисляет параметры регулятора, используя несколько различных методов настройки.

Перед началом работы системы пользователю предлагается меню для ввода априорной информации об объекте регулирования:

• диапазон изменения входного и выходного сигналов объекта;

• тип процесса в объекте управления (интегрирующий или нет);

• желаемые единицы измерения;

• структура контроллера (идеальная, последовательная или параллельная);

• частота дискретизации;

• постоянная времени фильтра в измерительном канале.

Идентификация выполняется с помощью анализа реакции на входной скачок в замкнутом или разомкнутом контуре (по выбору пользователя). Рекомендуется вариант в разомкнутом контуре. После того как пользователь нажимает кнопку «Старт», входной и выходной сигнал отображаются на экране компьютера.

Имеются некоторые возможности предварительной обработки собранных данных. К ним относятся удаление грубых ошибок измерений и выбросов, связанных с импульсными помехами, а также цифровая фильтрация. Это позволяет выполнять эксперименты в реальных условиях индустриального окружения.

После предварительной обработки данных Protuner выполняет расчёт частотной характеристики объекта, которая может быть отображена в виде диаграммы Боде, Найквиста или Никольса. Отображаются также статический коэффициент передачи, постоянные времени и транспортная задержка, частота ω₁₈₀ и период T₁₈₀.

Параметры ПИД-регулятора вычисляются по частотным характеристикам. Сначала вычисляются постоянная интегрирования и постоянная дифференцирования, затем на основе заданного запаса по фазе и усилению вычисляется пропорциональный коэффициент регулятора.

Качество регулирования задаётся в виде понятий «сильно демпфированная» переходная характеристика, «слабо демпфированная» и «быстрая» (с коэффициентом затухания 1/0,38).

Protuner даёт разные коэффициенты регулятора для реакции на изменение уставки и нагрузки.

Имеются средства для моделирования системы до записи параметров в ПИД-контроллер. Могут быть также построены частотные характеристики замкнутой системы, которые позволяют оценить полученный запас по фазе и усилению.

Заключение

Дифференциальный член в ПИД-регуляторах всегда реализуется совместно с фильтром, иначе вместо производной на выходе дифференциатора получаются только шумы. Интегральное насыщение является одной из причин ухудшения качества переходного процесса, сильно отличающегося от расчёта по линейной модели регулятора. Запас устойчивости и робастность являются параметрами, о которых часто забывают, однако построение регулятора для ответственных применений невозможно без детального анализа этих параметров, что можно выполнить с помощью коммерческих программных пакетов для настройки ПИД-регуляторов.

При формулировании критериев настройки ПИД-регулятора необходимо принимать во внимание реакцию не только на изменение уставки, но и на внешние возмущения. Выбор критериев качества регулирования должен исходить из смысла решаемой задачи. Несмотря на давность разработки, множество недостатков и наличие большого количества новых методов настройки, по-прежнему наиболее популярным является метод Зиглера-Никольса. Однако часто он используется только для генерации начальных приближений параметров, которые затем уточняются методами оптимизации и с помощью нечётких правил.

Автоматическая настройка и адаптация являются самыми актуальными задачами при построении ПИД-регуляторов. Несмотря на большое количество коммерческих продуктов, остаётся много нерешённых проблем, связанных с качеством настройки, влиянием нелинейностей объекта управления и внешних возмущений в процессе идентификации. При автоматической настройке и адаптации используются те же методы идентификации и расчёта параметров регулятора, что и при ручной настройке, однако они выполняются в автоматическом режиме. Наиболее эффективны методы автоматической настройки с применением компьютера, временно включённого в контур регулирования. Благодаря большой мощности процессора и отсутствию ограничений на объём программы появляется возможность создания программного средства с широкими сервисными свойствами и качественной математической обработкой.

Обзор публикаций

Методы оценки запаса устойчивости и робастности для нескольких наиболее популярных методик настройки ПИД-регуляторов с объектом первого порядка с задержкой описаны в работе [14]; в [15, 16] предложен метод расчёта параметров для объекта произвольного порядка при заданной робастности системы; в [17] использованы генетические алгоритмы для расчёта параметров ПИД-регулятора при заданных робастности и запасе устойчивости. В [18] дан обзор методов, а в [19] – новый метод предотвращения интегрального насыщения; в работе [20] исследована причина плохой робастности предиктора Смита к разбросу транспортной задержки и предложены методы её улучшения.

Методика настройки ПИД-регулятора для системы второго порядка с помощью методов оптимизации и с учётом ограничений в виде заданной робастности и полосы пропускания системы предложена в работе [21]. В [22] предложен метод расчёта параметров ПИД-регулятора как для устойчивых, так и для неустойчивых объектов после идентификации в разомкнутом контуре, а в [23] – для регулятора с внутренней моделью. В [18] также дана классификация методов настройки и получен новый метод для систем с транспортной задержкой. В [24] изложен новый метод настройки ПИД-регулятора, в котором вместо модели объекта управления используется интеграл Боде, при настройке учитывается запас по фазе и усилению.

Большинство методов настройки ПИД-регуляторов описаны в работах по адаптивным и самонастраивающимся регуляторам.

Программные средства настройки ПИД-регуляторов с помощью компьютера описаны в следующих работах: в [25] – программа для идентификации линейных систем, которая включает в себя обработку сигналов, построение графиков и идентификацию; в [26, 27] – системы для идентификации моделей и настройки параметров ПИД-регулятора, включающие устройства ввода-вывода и компьютер; в [13] дан обзор коммерческих программных продуктов. На упомянутом в статье сайте www.protuner.com в Application manual описана система для автоматической настройки ПИД-регуляторов.

Большое число публикаций посвящено методам автоматической настройки ПИД-регуляторов. В работе [28] предложен процесс автоматической настройки, нацеленный на получение эффективного ослабления внешних возмущений; в [29] – метод автонастройки для нелинейных систем, основанный на запоминании истории процесса и построении локальных моделей на основе накопленных данных о сигналах на входе и выходе системы.

Некоторые методы используют автоматическую настройку с идентификацией в замкнутом контуре регулирования в процессе нормального функционирования системы [30, 31]. В [32] предложен итерационный метод для автоматической настройки ПИД-регулятора, не требующий идентификации модели. В работах [33, 34] для автоматической настройки используются методы оптимизации.

Адаптивная настройка предиктора Смита описана в работе [35]; с применением базы нечётких правил – в [36], а для систем с неизвестной транспортной задержкой – в [37]. Большое количество методов автоматической настройки использует нечёткую логику, нейронные сети и генетические алгоритмы, они представлены в [38, 35, 39]. ●

Литература

8. Ziegler J.G., Nichols N.B. Optimum settings for automatic controllers // Trans. ASME. 1942. Vol. 64. P. 759-768.

9. Chien K.L., Hrones J.A., Reswick J.B. On automatic control of generalized passive systems // Trans. ASME. 1952. Vol. 74. P. 175-185.

10. Справочник по теории автоматического управления / Под ред. А.А. Красовского. – М. : Наука, 1987. – 712 с.

11. O’Dwyer A. PID compensation of time delayed processes 1998-2002: a survey // Proceedings of the American Control Conference, 4-6 June 2003. Vol. 2. P. 1494-1499.

12. Li Y., Ang K.H., Chong G.C.Y. Patents, Software, and Hardware for PID control: an overview and analysis of the current art // IEEE Control Systems Magazine. Feb. 2006. P. 42-54.    

13. Ang K.H., Chong G., Li Y. PID control system analysis, design, and technology // IEEE Trans. on Control Systems Technology. July 2005. Vol. 13. No. 4. P. 559-576.

14. Silva G.J., Datta A., Bhattacharyya S.P. On the stability and controller robustness of some popular PID tuning rules // IEEE Trans. on Automatic Control. Sept. 2003. Vol. 48. No. 9. P. 1638-1641.

15. Ho M.-T., Lin C.-Y. PID controller design for robust performance // IEEE Trans. on Automatic Control. Aug. 2003. Vol. 48. No. 8. P. 1404-1409.

16. Keel L.H., Rego J.I., Bhattacharyya S.P. A new approach to digital PID controller design // IEEE Trans. on Automatic Control. April 2003. Vol. 48. No. 4. P. 687-692.

17. Obika M., Yamamoto T. An evolutionary design of robust PID controllers // Mechatronics and Automation, 2005 IEEE International Conference, 29 July - 1 Aug. 2005. Vol. 1. P. 101-106.

18. Moradi M.H. New techniques for PID controller design // Proceedings of 2003 IEEE Conference on Control Applications (CCA 2003), 23-25 June 2003. Vol. 2. P. 903-908.

19. Hodel A.S., Hall C.E. Variable-structure PID control to prevent integrator windup // IEEE Trans. on Industrial Electronics. 2001. Vol. 48. No. 2. P. 442-451.

20. Shouli W., Watanabe K., Muramatsu E., Ariga Y., Endo S. Robust stability of approximate Smith predictor control systems // SICE 2004 Annual Conference, 4-6 Aug. 2004. Vol. 2. P. 1522-1527.

21. Jing-Chung Shen, Huann-Keng Chiang. PID tuning rules for second order systems // Control Conference, 2004 (5th Asian), 20-23 July 2004. Vol. 1. P. 472-477.

22. Silva G.J., Datta A., Bhattacharyya S.P. New results on the synthesis of PID controllers // IEEE Trans. on Automatic Control. Feb. 2002. Vol. 47. No. 2. P. 241-252.

23. Skoczowski S., Domek S., Pietrusewicz K., Broel-Plater B. A method for improving the robustness of PID control // IEEE Trans. on Industrial Electronics. Dec. 2005. Vol. 52. No. 6. P. 1669-1676.

24. Karimi A., Garcia D., Longchamp R. PID controller tuning using Bode’s integrals // IEEE Trans. on Control Systems Technology. Nov. 2003. Vol. 11. No. 6. P. 812-821.

25. Sanchez-Gasca J.J., Clark K., Miller N.W., Okamoto H., Kurita A., Chow J.H. Identifying linear models from time domain simulations // IEEE Computer Applications in Power. Apr. 1997. Vol. 10. No. 2. P. 26-30.

26. Hemerly E.E. PC-based packages for identification, optimization, and adaptive control // IEEE Control Systems Magazine. Feb. 1991. Vol. 11. Issue 2. P. 37-43.

27. Oviedo J.J.E., Boelen T., van Overschee P. Robust advanced PID control (RaPID): PID tuning based on engineering specifications // IEEE Control Systems Magazine. Feb. 2006. Vol. 26. Issue 1. P. 15-19.

28. Leva A. Autotuning process controller with enhanced load disturbance rejection // American Control Conference, 30 June - 2 July 2004. Proceedings. Vol. 2. P. 1400-1405.

29. Takao K., Yamamoto T., Hinamoto T. Design of a memory-based self-timing PID controller // 43rd IEEE Conference on Decision and Control (CDC 2004), 14-17 Dec. 2004. Vol. 2. P. 1598-1603.

30. Qiwen Yang, Yuncan Xue, Jiao Huang. Simultaneous PID self-tuning and control // Proceedings of the 2004 IEEE International Symposium on Intelligent Control, 2-4 Sept. 2004. P. 363-367.

31. Ho H.F., Wong Y.K., Rad A.B. Adaptive PID controller for nonlinear system with H∞ Physics and Control, 2003 International Conference, 20-22 Aug. 2003. Proceedings. Vol. 4. P. 1315-1319.

32. Calcev G., Gorez R. Iterative technique for PID controller tuning // Proceedings of the 34th IEEE Conference on Decision and Control, 13-15 Dec. 1995. Vol. 3. P. 3209-3210.

33. Glickman S., Kulessky R., Nudelman G. Identification-based PID control tuning for power station processes // IEEE Trans. on Control System Technology. 2004. Vol. 12. No. 1. P. 123-132.

34. Rad A.B., Lo W.L., Tsang K.M. Self-tuning PID controller using Newton-Raphson search method // IEEE Trans. on Industrial Electronics. Oct. 1997. Vol. 44. No. 5. P. 717-725.

35. Jih-Jenn Huang, DeBra D.B. Automatic Smith-predictor tuning using optimal parameter mismatch // IEEE Trans. on Control Systems Technology. May 2002. Vol. 10. No. 3. P. 447-459.

36. Ivanova E., Hadjiski M. Rules based adaptation of Smith predictor // Intelligent Systems, First International IEEE Symposium, 2002. Proceedings. Vol. 3. P. 26-30.

37. Ren X.M., Rad A.B., Lo W.L., Chan P.T. Adaptive H/sub 2/ optimal control based on Smith predictor for continuous-time systems with unknown time delay // International Conference on Control and Automation (ICCA ‘05), 26-29 June 2005. Vol. 1. P. 159-164.

38. Hsuan-Ming Feng. A self-tuning fuzzy control system design // IFSA World Congress and 20th NAFIPS International Conference, 25-28 July 2001. Vol. 1. P. 209-214.

39. Pin-Yan Tsai, Huang-Chu Huang, Shang-Jen Chuang, Yu-Ju Chen, Rey-Chue Hwang. The model reference control by adaptive PID-like fuzzy-neural controller // IEEE International Conference on Systems, Man and Cybernetics, 10-12 Oct. 2005. Vol. 1. P. 239-244