Концепции числового программного управления технологическим оборудованием
Разработчики современных систем числового программного управления (ЧПУ) выделяют 5 основных архитектурных вариантов, которые существуют на рынке [1]. Первый вариант – это классические системы CNC (Computer Numerical Control). Такие системы выпускаются фирмами с богатой традицией производства высококачественной собственной микроэлектронной аппаратуры. Однако эти фирмы под влиянием пользователей технологического оборудования, желающих иметь гибкий интерфейс оператора, предлагают модификацию PCNC-1 (Personal Computer Numerical Control) с персональным компьютером в качестве терминала (второй вариант). Следующим шагом в развитии систем с ЧПУ стала реализация двухкомпьютерного варианта PCNC-2 (третий вариант). Несколько позже появились системы PCNC-3, ядро которых реализовано на отдельной плате, устанавливаемой в корпусе промышленного персонального компьютера (четвёртый вариант). С бурным развитием микропроцессорной техники и повышением производительности микропроцессоров всё большее распространение получает однокомпьютерный (пятый) вариант системы PCNC-4, особенность которого заключается в том, что все задачи управления (геометрическая, логическая, терминальная) решаются программным путём без какой-либо дополнительной аппаратной поддержки.
Требования к программно-аппаратному комплексу
Анализ рынка отечественных разработок систем класса PCNC показал, что подавляющее большинство применяемых сервоконтроллеров обычно выполняется из зарубежных модулей, где законы управления движением прошиты и недоступны пользователю для их модификации. Отечественные же разработки ограничены лишь двумя видами интерполяции – линейной и круговой, а также ставшими уже классическими прямоугольным и трапецеидальным законами разгона/торможения. В ряде случаев, например в установках лазерного раскроя листовых материалов или гравировки, классические законы управления следящими электроприводами не позволяют достичь требуемых динамических характеристик электромеханических систем – минимальной ошибки отработки заданной траектории движения при максимальном быстродействии и ограничениях на скорость движения и ускорение. Так, при лазерном раскрое определённых материалов ошибки поддержания заданной контурной скорости могут привести к значительному оплавлению кромки материала либо отклонению от заданной глубины резки.
С целью разработки и исследования перспективных алгоритмов управления движением исполнительных электроприводов следящих электромеханических систем сотрудниками кафедры электропривода и электрооборудования Томского политехнического университета был разработан программно-аппаратный комплекс. В основе комплекса лежит программно реализованный сервоконтроллер с открытой архитектурой, то есть доступный любому пользователю для изменения. Для достижения поставленной цели были определены следующие задачи и требования к программно-аппаратному комплексу:
-
техническая реализация исследовательского комплекса на основе однокомпьютерного варианта системы управления;
-
разработка программного обеспечения, реализующего алгоритмы линейной, круговой и сплайн-интерполяции, с возможностью дальнейшей доработки другими пользователями;
-
программная реализация алгоритмов следящего контура и сигнальной адаптации к изменению управляющих сигналов;
-
обеспечение возможности сопоставления результатов эксперимента и моделирования в среде MatLab;
-
минимизация стоимости системы управления.
Дополнительной задачей, возлагаемой на комплекс, является обеспечение возможности проведения лабораторных и практических занятий для некоторых учебных дисциплин электротехнического направления.
Аппаратные средства
Исследовательский комплекс имеет двухуровневую структуру (рис. 1). Нижний уровень содержит датчики, исполнительный механизм и регулируемые электроприводы. Верхний уровень реализован на базе персонального компьютера со встроенными модулями ввода-вывода формата MicroPC.
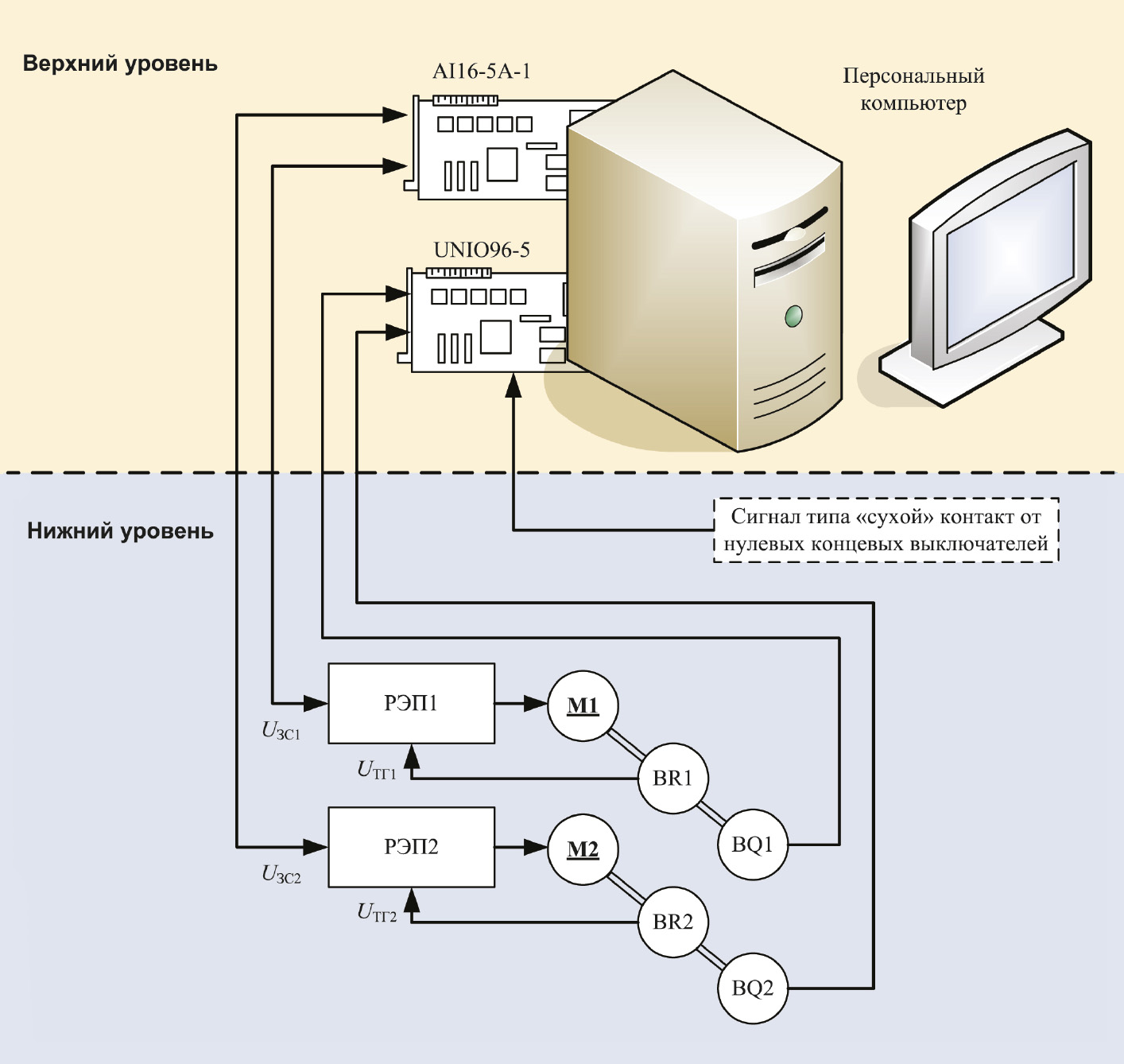
Условные обозначения: РЭП1, РЭП2 — регулируемые электроприводы; M1, M2 — электродвигатели; BR1, BR2 — тахогенераторы; BQ1, BQ2 — датчики положения; UЗС1, UЗС2 — управляющие сигналы для РЭП; UТГ1, UТГ2 — сигналы обратной связи с тахогенераторов.
Исполнительным механизмом исследовательского комплекса является двухкоординатный стол (рис. 2) с коэффициентами передачи редукторов i по осям X и Y, равными 12 (шаг винта tв = 6 мм).

Каждую из координат обслуживает свой электродвигатель постоянного тока 1ПИ12. В качестве регулируемых электроприводов (РЭП1, РЭП2) используются тиристорные электроприводы «КЕМЕК» (рис. 3).

Электропривод такого типа является типичным представителем быстродействующих широкорегулируемых приводов с однозонным регулированием скорости для механизмов станков и промышленных роботов. Диапазон регулирования скорости электропривода составляет не менее 2000.
Устройство числового программного управления выполнено на базе персонального компьютера и двух модулей MicroPC фирмы Fastwel (рис. 4): модуля UNIO96-5 для ввода-вывода дискретных данных и модуля AI16-5A-1 для ввода-вывода аналоговой информации.

Выбор модуля AI16-5A-1 обусловлен в первую очередь наличием в комплексе двух аналоговых электроприводов, для управления которыми у данного модуля есть два канала ЦАП, а также возможностью цифрового преобразования в модуле аналоговых сигналов регулируемого электропривода.
Программируемый модуль UNIO96-5 был выбран в силу необходимости вводить и обрабатывать отличающиеся по формату дискретные сигналы от концевых выключателей и двух датчиков положения. Дискретные сигналы от нулевых концевых выключателей двухкоординатного стола представляют собой сигналы типа «сухой» контакт, а выходным сигналом датчика положения является последовательность электрических импульсов прямоугольной формы уровня TTL (в качестве датчиков положения применены преобразователи углового перемещения ЛИР-128А фирмы СКБ ИС с разрешающей способностью 2500 импульсов на оборот; перемещению по каждой оси на 1 мкм с учётом коэффициента передачи механизма соответствует выходная последовательность из 5 импульсов). Применение модуля UNIO96-5 для обработки сигналов датчиков позволяет снизить нагрузку на центральный процессор персонального компьютера. Так, благодаря использованию программируемых логических матриц (FPGA) и технологии ISP задача подсчёта поступающих импульсов и определения направления вращения вала двигателя решается с помощью стандартной прошивки «X32», реализующей на базе FPGA модуля два 32-разрядных счётчика импульсов энкодера. Аналогично с использованием стандартной прошивки «N04», реализующей формирователь прерываний по событиям с программируемым антидребезгом по 24 каналам, осуществляется обработка дискретных сигналов от концевых выключателей.
Программное обеспечение
Программное обеспечение верхнего уровня разработано в среде Delphi 7 и работает под управлением операционной системы Windows XP. Представление об интерфейсе пользователя разработанной программы даёт рис. 5.
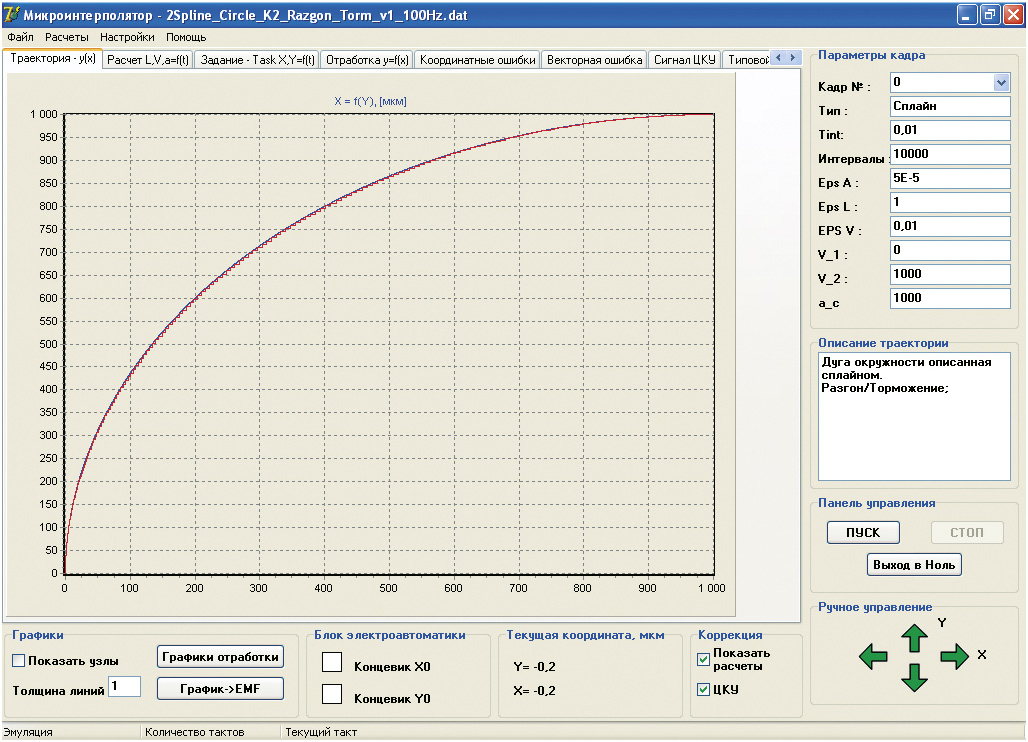
Функциональные возможности программного обеспечения верхнего уровня:
-
создание библиотеки траекторий заданного движения электроприводов;
-
сохранение и отображение результатов эксперимента (массивов заданий и отработки по положению, скоростей, координатных, контурных и векторных ошибок, сигналов цифровой коррекции);
-
скачкообразное и линейное изменение управляющего воздействия в режиме типовых экспериментов (рис. 6);
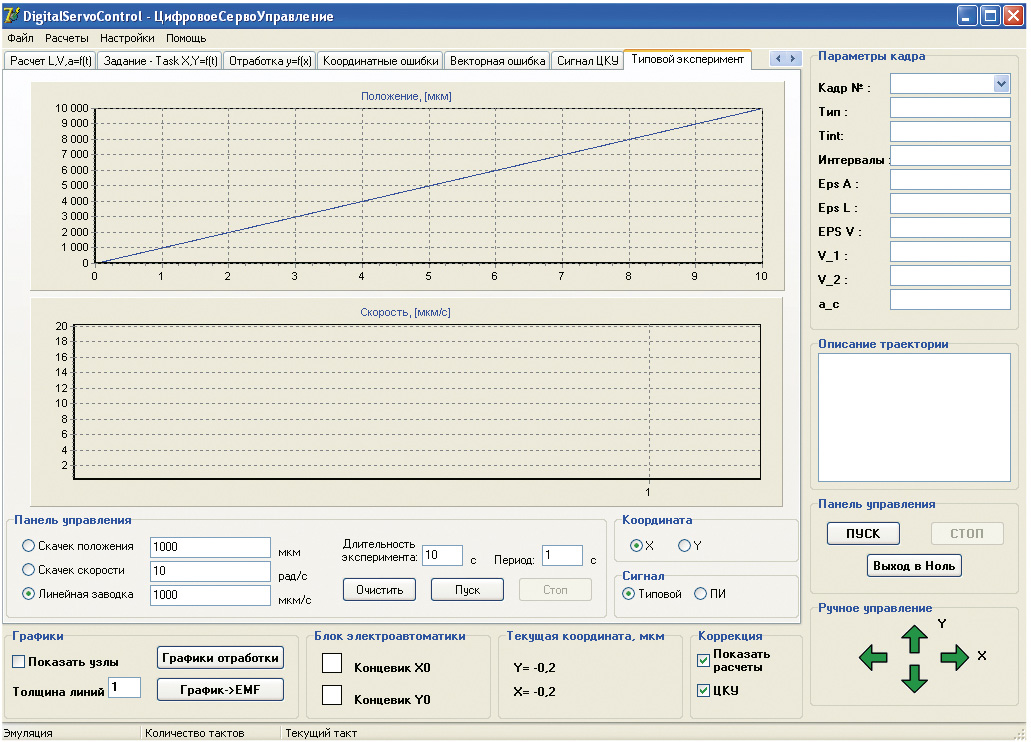
-
перемещение в пределах рабочей зоны с помощью кнопок управления в режиме ручного управления;
-
отображение состояния концевых выключателей и текущей координаты;
-
исследование влияния параметров цифрового контура положения (коэффициентов регуляторов положения по обеим осям, частот квантования по времени и по уровню в контуре положения, коэффициентов цифрового корректирующего устройства) на координатные и контурные ошибки системы;
-
автонастройка и изменение адресного пространства ввода-вывода модулей AI16-5A-1 и UNIO96-5.
Основным недостатком программного обеспечения, функционирующего под управлением многозадачной операционной системы Windows XP, является отсутствие гарантированного срабатывания программы в заданный момент времени [2]. Поэтому систему управления, использующую такое программное обеспечение, можно с натяжкой назвать лишь системой «мягкого» реального времени, то есть системой, иногда допускающей запаздывание реакции на какое-либо внешнее воздействие.
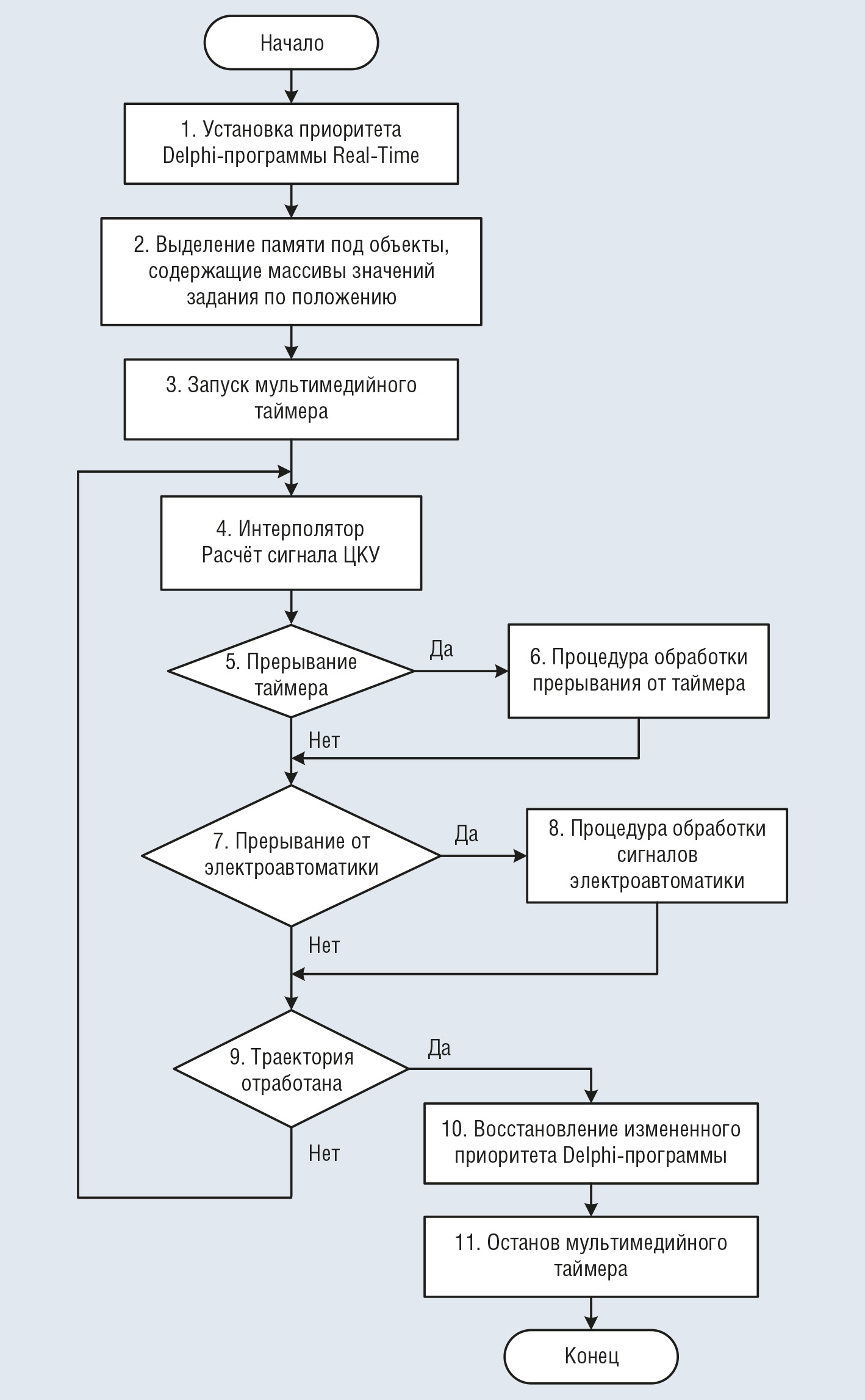
С учётом описанных особенностей аппаратной реализации комплекса предложен алгоритм главного цикла программы управления экспериментальной установкой (рис. 7). Для обеспечения своевременного формирования задания на РЭП приоритет запущенной программы повышен до уровня Real-Time. Однако нужно помнить, что установка приоритета реального времени в среде Windows XP не гарантирует своевременного расчёта значений сигнала задания, поэтому предлагается программно перераспределить вычислительные ресурсы между процессами расчёта интерполяционного полинома и расчёта значений сигнала цифрового корректирующего устройства (ЦКУ). Таким образом, расчёт задания для электроприводов ведётся с опережением и занимает всё доступное процессорное время, кроме случая обработки прерываний таймера и электроавтоматики.
В соответствии с рекомендациями компании Microsoft было решено отказаться от стандартных таймеров Delphi и перейти к непосредственному использованию мультимедийного таймера [3]. Такой подход существенно повышает вероятность своевременной выдачи управляющего сигнала на регулируемые электроприводы. Оценка работы мультимедийного и программного таймера Delphi с приоритетом Real-Time приведена в табл. 1.
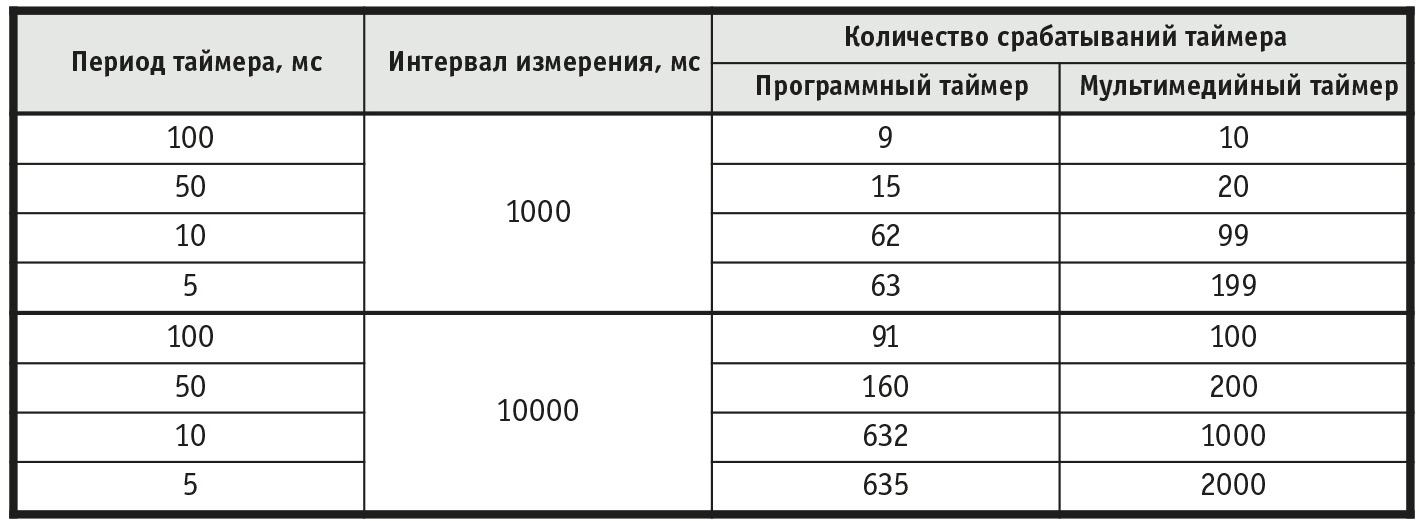
Полученные результаты отражают тот факт, что даже с установленным высоким приоритетом программный таймер не обеспечивает заданное количество срабатываний таймера за отведённый промежуток времени. Некорректное срабатывание таймера, в конечном счёте, приводит к запаздыванию при формировании задания для регулируемых электроприводов, что обуславливает возникновение рывков скорости и ударов в механической части системы. В результате возможно искажение траектории движения многокоординатного электропривода и снижение качества обрабатываемого изделия.
Экспериментально установлено, что для частоты квантования в контуре положения в пределах до 200 Гц работа мультимедийного таймера позволяет гарантированно выдавать задание на регулируемые электроприводы с заданной полосой пропускания. Применение частот квантования в контуре положения свыше 200 Гц в программно-аппаратных системах управления данной архитектуры является неоправданным вследствие значительного влияния на работу таймера таких процессов, как навигация в меню программного обеспечения и вызов других программ.
Пример работы с мультимедийным таймером и системой приоритетов в Delphi:
hProcess:=GetCurrentProcess;
SetPriorityClass(hProcess, REALTIME_PRIORITY_CLASS);
MMTimer1:=timeSetEvent(Delay,Res, @TimerCall,100,TIME_PERIODIC);
timeKillEvent(MMTimer1);
Оператор в первой строке позволяет получить доступ к запущенному процессу. Оператор во второй строке, в свою очередь, устанавливает указанному процессу приоритет реального времени. В третьей строке показан пример вызова функции инициализации мультимедийного таймера. Основными параметрами являются Delay – период срабатывания таймера [мс], Res – разрешающая способность таймера [мс], TIME_PERIODIC – параметр, указывающий, что срабатывание таймера будут происходить с периодом Delay до тех пор, пока таймер не будет остановлен.
Алгоритмическое обеспечение
В основе программного обеспечения комплекса используются разработанные авторами статьи алгоритмы кубической сплайн-интерполяции, управления положением многокоординатного электропривода и сигнальной адаптации следящих систем.
В общем виде кубическим сплайном, интерполирующим на отрезке [a, b] данную функцию f(x), называется функция вида:
g(x) = gk(x) = ak+bk(x–xk)+ck(x–xk)2+dk(x–xk)3 при x ∈ [xk–1,xk], k=1…n, (1)
удовлетворяющая совокупности следующих условий:
а) g(xk) = fk (условие интерполяции в узлах сплайна);
б) g(x) ∈ C2 [a, b] (двойная непрерывная дифференцируемость);
в) g˜(a) = g˜(b) = 0 (краевые условия).
Для расчёта коэффициентов ak, bk, ck, dk и построения такого сплайна существует несколько методов, например метод прогонки. Существенными недостатками подобных методов являются значительное время расчёта вследствие наличия двух циклов прогонки (прямого и обратного), а также громоздкость вычислительного алгоритма. С целью снижения требований к вычислительным устройствам авторами предложен алгоритм расчёта коэффициентов, который не требует наличия двух циклов прогонки. Отличительной особенностью предлагаемого алгоритма является то, что для уменьшения времени нахождения коэффициентов исходная последовательность точек xn разбивается на интервалы, содержащие по четыре точки. Для каждого из этих интервалов определяются непосредственные значения коэффициентов через выражения, аналитически выведенные для каждого коэффициента. Выражения для расчёта коэффициентов и блок-схема алгоритма построения сплайн-функции приведены в работе [4].
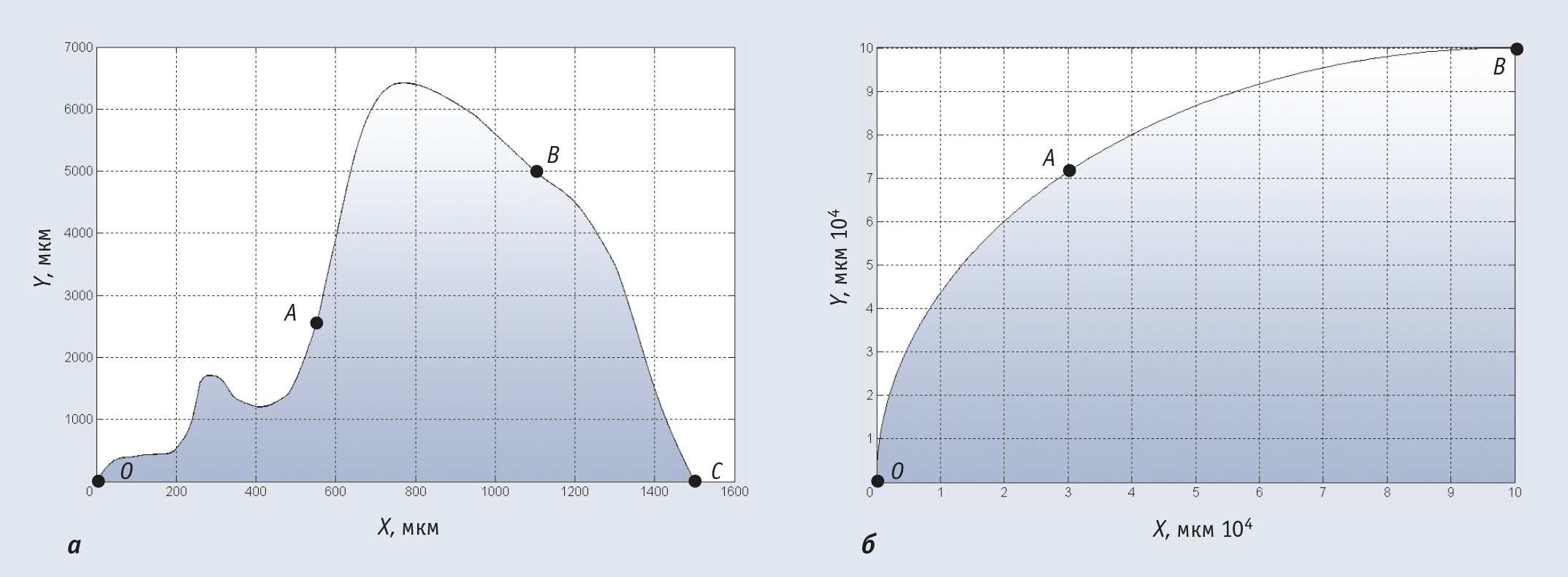
Примеры отработки траекторий движения, представленных сплайном, показаны на рис. 8. График отработанной траектории движения на плоскости XY построен по информации, полученной от дискретных датчиков положения. Частота дискретизации данных положения вала двигателя по времени равна 100 Гц. В первом случае (рис. 8 а) траектория была сформирована тремя сплайнами. На начальном участке траектории OA производится разгон по параболическому закону изменения ускорения во времени. По окончании разгона оставшийся участок OA траектории отрабатывается с постоянной заданной контурной скоростью. Следующий участок траектории – AB также отрабатывается с заданной постоянной контурной скоростью. На участке BC происходит торможение до заданной контурной скорости. Момент начала торможения спрогнозирован алгоритмом управления скоростью на участках разгона/торможения. Во втором случае (рис. 8 б) траектория была задана двумя сплайнами. Первый участок траектории, обозначенный точками OA, содержит два интервала – разгон и движение с постоянной контурной скоростью. Второй участок – AB содержит также два интервала: интервал движения с постоянной контурной скоростью и интервал торможения по параболическому закону изменения ускорения во времени.
Ключевым моментом в описанных примерах отработки траекторий движения является проверка не только работоспособности алгоритмов интерполяции, но и моментов стыковки различных участков разгона/торможения и перехода с одной контурной скорости на другую (точки O, A, B, C). В отличие от классических алгоритмов, формирующих законы разгона/торможения, где присутствуют скачки скорости, неизбежно приводящие к искажению траектории движения, в данном случае контурные ошибки уменьшаются на 12,5%.
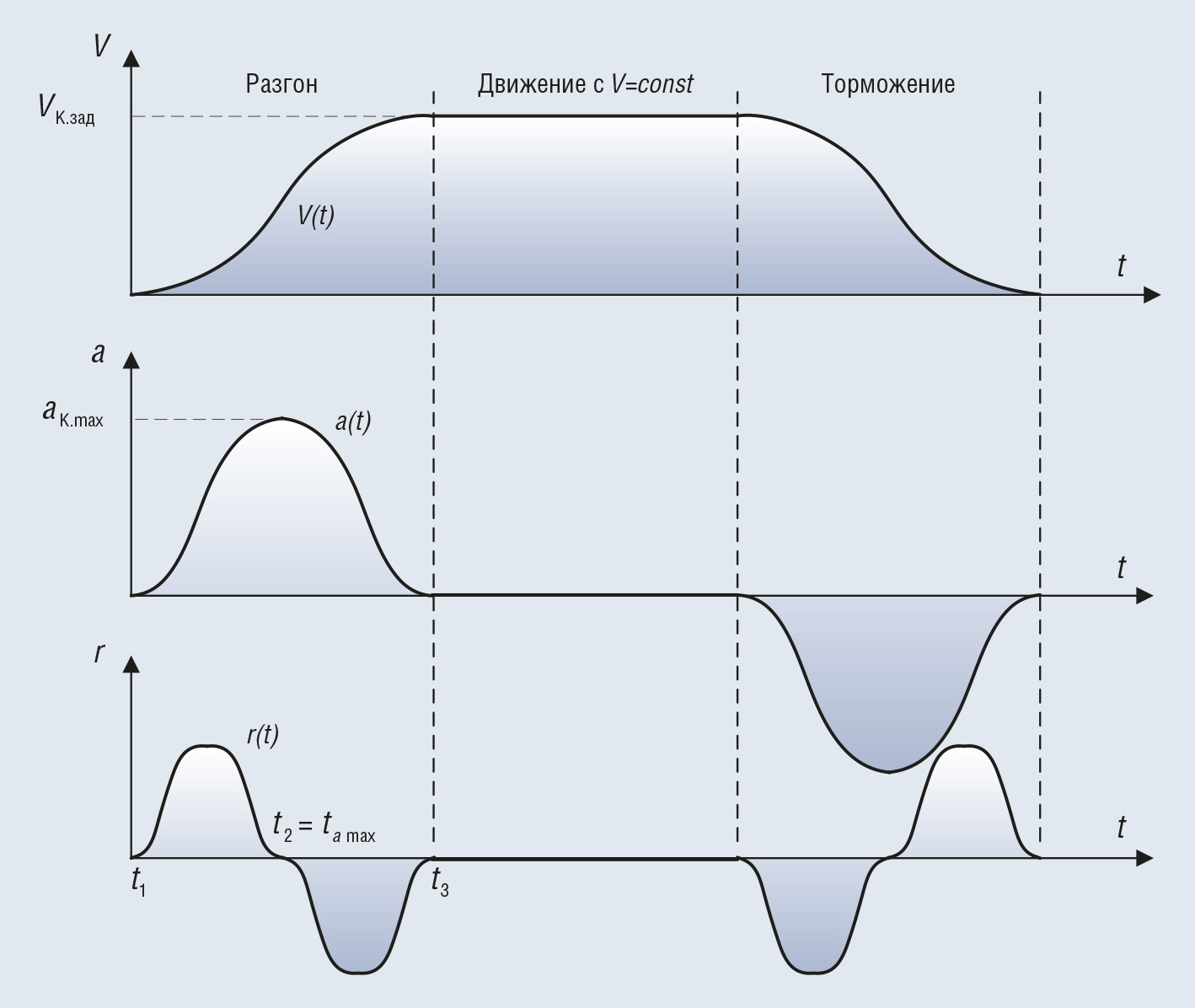
С целью повышения плавности движения исполнительного механизма в динамических режимах, обусловленных участками разгона или торможения, предложен алгоритм управления контурной скоростью движения, который учитывает ограничение рывка на интервалах разгона/торможения, как показано на рис. 9. Вопросам формирования диаграмм управляющего воздействия в следящем электроприводе (ЭП) посвящено много работ. В частности, в одной из работ Сабинина Ю.А. [5], посвящённой формированию задающего воздействия, проводится сравнительная оценка треугольной, параболической, кубической и косинусоидальной диаграммы скорости электропривода. Критерием оптимальности, определяющим качество работы следящей системы, принимается отсутствие резких изменений ускорения ЭП, которые неизбежно приводят к появлению упругих колебаний в механической части системы. Авторами было установлено, что выбранным критериям, помимо диаграмм с линейным нарастанием ускорения удовлетворяют параболическая диаграмма ускорения, вариант в виде суммы кубической и квадратичной зависимости и вариант косинусоидальной диаграммы. С практической точки зрения представляет интерес реализация подобных алгоритмов не только в системах класса PCNC, но и в классических CNC, поскольку в отечественных разработках до сих пор отдаётся приоритет трапецеидальным диаграммам скорости при разгоне/торможении.
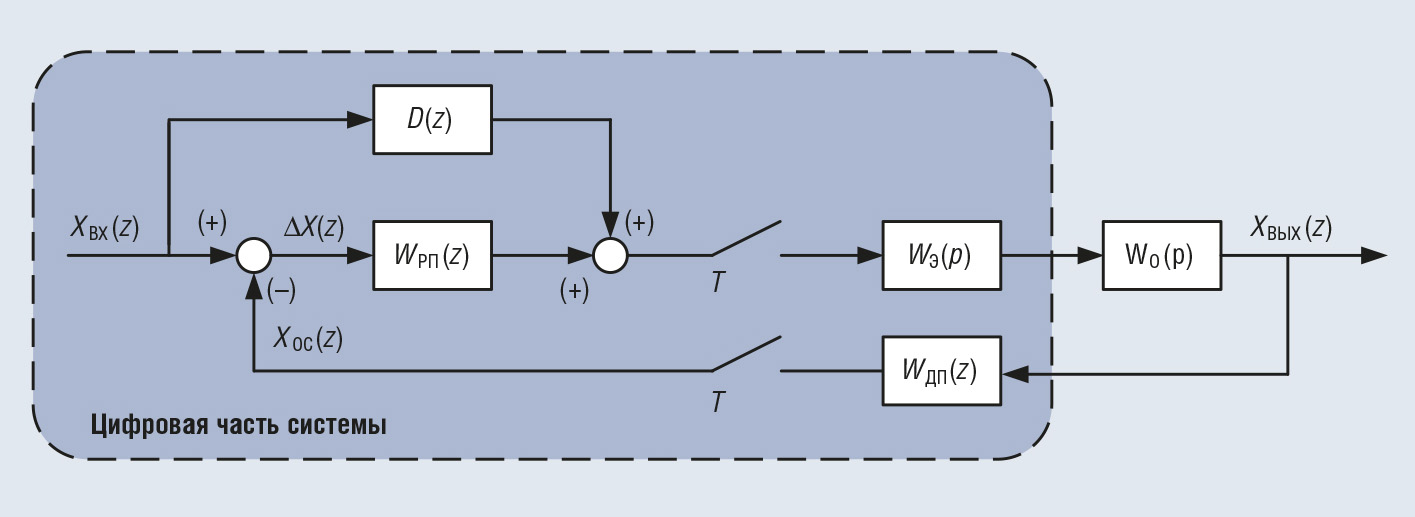
Условные обозначения: WДП(z) — единичная передаточная функция датчика положения; WРП(z) — передаточная функция регулятора положения; D(z) — ЦКУ; WЭ(p) — экстраполятор нулевого порядка; WО(p) — передаточная функция непрерывной части системы.
Программно реализованный алгоритм сигнальной адаптации представляет собой цифровое корректирующее устройство задающих сигналов для следящего электропривода. Упрощённая структурная схема следящего электропривода с ЦКУ приведена на рис. 10. Введение ЦКУ позволяет обеспечить сигнальную адаптацию с вычислением первой, второй и третьей производных задающего воздействия. Такой электропривод является комбинированной следящей системой, обеспечивающей инвариантность относительно задающего воздействия третьего порядка. Дискретная передаточная функция ЦКУ имеет вид:
D(ζ)=α1·(1–ζ–1)+α2·(1–ζ–1)2+α3·(1–ζ–1)3. (2)
Здесь α1, α2, α3 — коэффициенты ЦКУ, определяемые по выражениям (4) из условия абсолютной инвариантности следящего электропривода относительно задающего воздействия:
С0 = С1 = С2 = С3 = 0, (3)
где С0, С1, С2, С3 — коэффициенты установившейся ошибки по положению, скорости, ускорению и рывку в дискретные моменты времени.
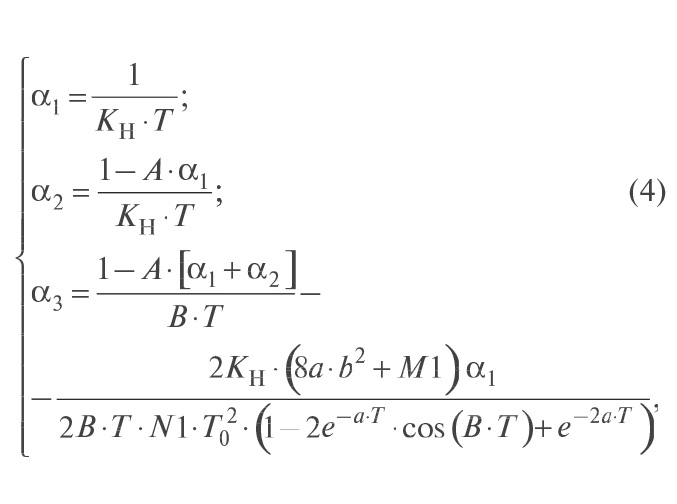
где T — период дискретизации в цифровом контуре положения; KH = KM/KC — коэффициент передачи непрерывной части системы; KM — коэффициент передачи механизма; KC —коэффициент обратной связи по скорости; T0=√TPC·T1; TPC— постоянная времени интегрирования ПИ-регулятора скорости; T1 — постоянная времени входного фильтра контура скорости, оптимизирующего реакцию системы на входное воздействие; a, b — вещественная и мнимая части комплексно-сопряжённых корней характеристического уравнения, полученного при преобразовании передаточной функции объекта управления из непрерывной области в Z-область; A, B, M1, N1 — полиномы, полученные в результате преобразования передаточной функции системы по ошибке.
Из выражений (2-4) видно, что коэффициенты ЦКУ зависят от частоты квантования в контуре положения, коэффициента регулятора положения и параметров регулируемого электропривода, но в то же время они не зависят от типа интерполятора.
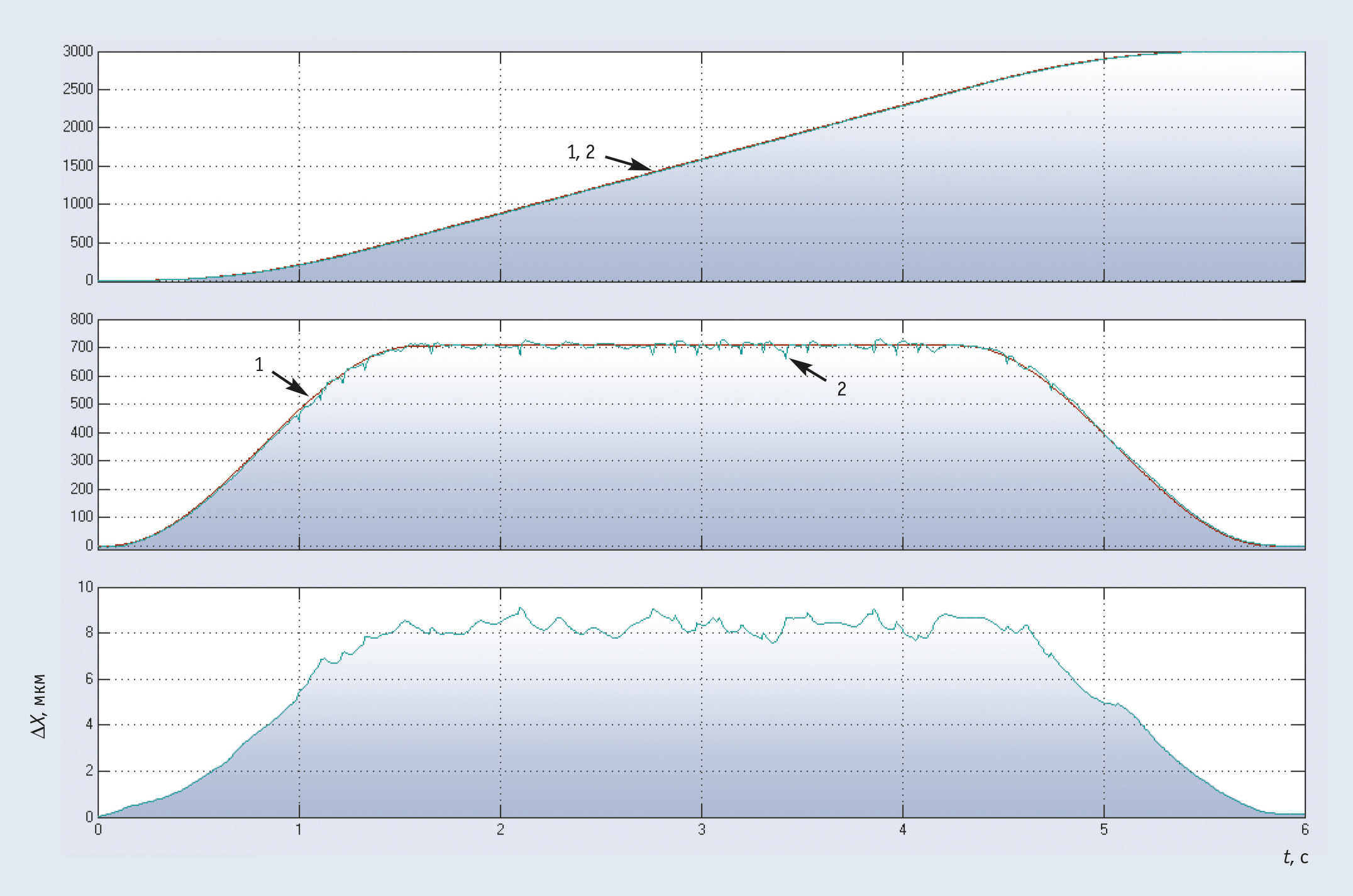
Условные обозначения: 1 — заданная траектория; 2 — отработанная траектория; ΔX — координатная ошибка; VXЗ, VXО — заданная и отработанная координатная скорость; XЗ, XО — заданное и отработанное перемещение
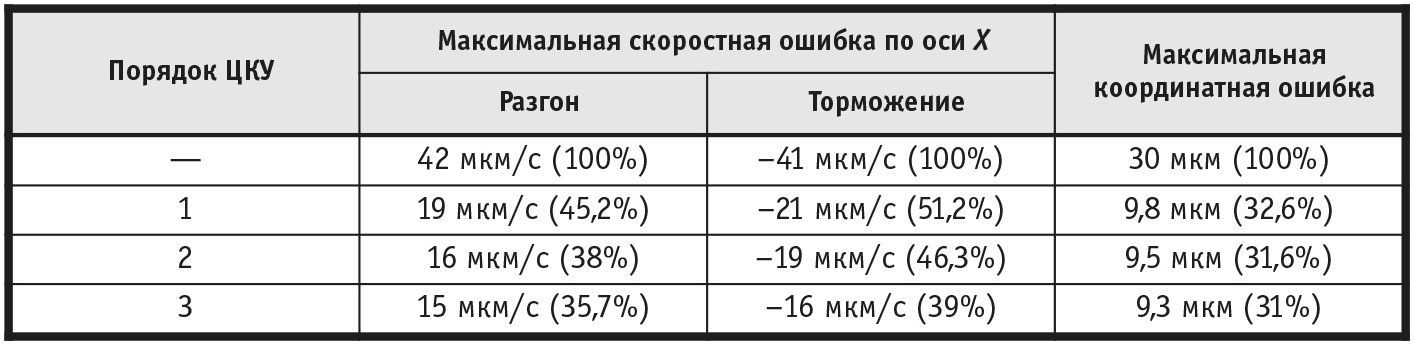
Пример отработки прямолинейной траектории движения по оси X, описанной сплайном с предложенным алгоритмом разгона/торможения и ЦКУ 3-го порядка в контуре положения, приведён на рис. 11. Верхний график показывает изменение во времени сигнала задания по координате X, а также сигнал обратной связи от датчика положения. Отсутствие перерегулирования по положению в сигнале обратной связи свидетельствует о правильно настроенном регуляторе положения и своевременно сформированном задании для электропривода. Средний график отражает изменение во времени заданной и отработанной координатной скорости регулируемым электроприводом по оси X. Нижний график показывает изменение координатной ошибки во времени. В данном случае мы видим, что максимальная координатная ошибка не превышает 9,3 мкм. В отсутствие же ЦКУ в контуре положения график изменения координатной ошибки имеет такой же вид, пропорциональный графику изменения координатной ошибки, с той лишь разницей, что максимальная величина координатной ошибки составляет 30 мкм. Полученные результаты эксперимента, свидетельствующие об эффективности введения цифровой коррекции в контур положения, сведены в табл. 2.
Заключение
Экспериментально установлено, что разработанное программное обеспечение, функционирующее под управлением многозадачной операционной системы Windows XP, может быть использовано для управления следящими электроприводами с частотой квантования в контуре положения до 200 Гц и точностью позиционирования 1 мкм. В качестве исполнительных электроприводов могут быть применены не только электроприводы постоянного тока, но и электроприводы с шаговыми и бесконтактными двигателями. При необходимости управления электроприводами с цифровым интерфейсом связи или внешними контроллерами электроавтоматики представленный в статье программно-аппаратный комплекс может быть оснащён соответствующими интерфейсами связи без изменения базовых алгоритмов управления.
Исследования показали эффективность предложенных алгоритмов управления движением. В частности, по сравнению с алгоритмом разгона/торможения с трапецеидальной диаграммой скорости предложенный алгоритм разгона/торможения позволил снизить упругие колебания в механической части системы, а также скачки скорости на участках стыковки интервалов разгона/торможения на 12,5% при одинаковой геометрии траектории движения.
Введение цифровой коррекции в контур положения позволило значительно снизить скоростную, координатную и контурную ошибки. Динамику изменений регулируемых величин при введении ЦКУ отражает табл. 2. Наибольший эффект при использовании цифровой коррекции даёт ЦКУ третьего порядка. Это позволяет уменьшить координатную ошибку на 69%, а скоростную ошибку на этапе разгона – на 64,3%. Введение ЦКУ второго порядка позволяет уменьшить координатную ошибку на 68,4%, а скоростную – на 62%. В свою очередь, введение ЦКУ первого порядка позволяет снизить координатную ошибку на 67,4%, а скоростную – на 54,8%. В общем случае эффект от использования цифровой коррекции задающих сигналов определяется заданной контурной скоростью и ускорением, а также геометрией траектории движения.
В настоящее время разработанный комплекс используется на кафедре электропривода и электрооборудования Томского политехнического университета в учебном процессе при проведении лабораторных занятий по курсам «Комплексная автоматизация технологических процессов» и «Автоматизированный электропривод типовых производственных механизмов».
Дальнейшее развитие данного комплекса связывается с его внедрением в системы управления лазерным раскроем листовых материалов и лазерной гравировки.
Основными конкурентными преимуществами комплекса являются полная открытость программного кода системы управления для модификации конечным пользователем, простота технической реализации системы управления и дальнейшего усовершенствования, отсутствие потребности в значительных капиталовложениях. ●
Литература
-
Сосонкин В.Л., Мартинов Г.М. Концепция числового программного управления мехатронными системами: анализ современного мирового уровня архитектурных решений в области ЧПУ // Мехатроника, автоматизация, управление. 2002. № 7. С. 11-17.
-
Сорокин С. Системы реального времени // Современные технологии автоматизации. 1997. № 2. С. 22-29.
-
Джордейн Р. Справочник программиста персональных компьютеров типа IBM PC, XT и AT: Пер. с англ. Предисл. Н.В. Гайского. — М. : Финансы и статистика, 1992. – 544 с.
-
Букреев В.Г., Гусев Н.В. Обзор методов интерполяции дискретных траекторий движения электромеханических систем // Деп. в ВИНИТИ 28.01.03, № 166-В2003. 2003. С. 1-31.
-
Денисова А.В., Сабинин Ю.А. Формирование задающих воздействий в позиционном электроприводе // Электротехника. 2002. № 9. С. 21-28.
Авторы — сотрудники Томского политехнического университета
Телефон: (3822) 56-3759
Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!