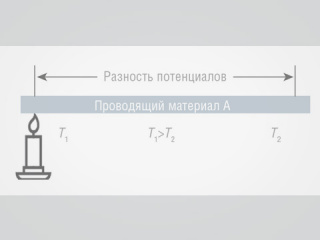
Термоэлектрический эффект был открыт случайно в 1821 году немецким физиком Томасом Иоганном Зеебеком в процессе эксперимента: небольшой кусок висмута припаивался с обоих концов к медной спирали. Если один его конец нагревался с помощью лампы, а другой оставался холодным, то магнитная стрелка, помещённая внутрь спирали, поворачивалась, указывая на прохождение тока, который в холодном спае шёл в направлении от меди к висмуту. Таким образом Зеебек экспериментально определил, что, когда концы проводника имеют разные температуры, между ними возникает разность потенциалов. Этот эффект назван эффектом Зеебека. Работа ученого показала также, что возникающее напряжение всегда пропорционально разнице температур. Его открытие вскоре легло в основу создания термопары, которая сегодня является одним из самых распространённых и экономичных датчиков температуры.

Итак, Зеебек провёл опыт (рис. 1), в ходе которого выяснил, что разность потенциалов между концами проводника V12 оказывается пропорциональна разности температур спаев (T1–T2), как это показано в формуле (1). Коэффициент пропорциональности Sa в этой зависимости – коэффициент
Зеебека, определяемый как термоэлектрическая способность пары. Его также называют коэффициентом термоЭДС.

Аналитическое объяснение эффекту Зеебека дают современные теории поведения электронов в молекулярной структуре материала. Точный математический описательный аппарат очень сложен и обращается к электронной квантовой теории, однако фундаментальная концепция проста. Молекулярные структуры электрических проводников таковы, что электроны в материале слабо связаны с их узлами-решётками (ядрами) и могут перемещаться по всему материалу под влиянием приложенной к проводнику разности потенциалов. Когда один конец проводящего материала нагревают до температуры, большей, чем на противоположном конце, электроны на горячем конце приобретают бо́льшую энергию, чем электроны на холодном конце. Эти более энергичные электроны начинают диффундировать к холодному концу. Процесс накопления заряда продолжается до тех пор, пока возникшая разность потенциалов не вызовет поток электронов в обратном направлении, равный первичному, благодаря чему установится равновесие. Следовательно, нагрев одного конца проводника вызывает разность потенциалов из-за перераспределения подогретых электронов в материале. Это и есть эффект Зеебека и основной принцип термопар.
Формула (1) обеспечивает аналитическое выражение для этого явления, а коэффициент Sa в ней скрывает все сложные квантовые электронные поведения в твёрдом теле и полностью зависит от молекулярной структуры материала. Как и следовало ожидать, термоэлектрическая способность (Sa) является нелинейной зависимостью от внутренней молекулярной структуры материала и его температуры.
Экспериментальная работа Зеебека показала, что если проводники цепи вольтметра и тестируемый проводник сделаны из одного материала, то напряжение в этой петле будет равно нулю: Sa×(T1−T2)+Sa×(T2−T1)=0. Напряжение в контуре появится только тогда, когда измерения будут проводиться на открытых концах двух разнородных проводников, соединённых с другого конца, при наличии разности температур этих соединений. Топология этой ситуации показана на рис. 2, иллюстрирующем типичное подключение термопары для измерения разности температур.
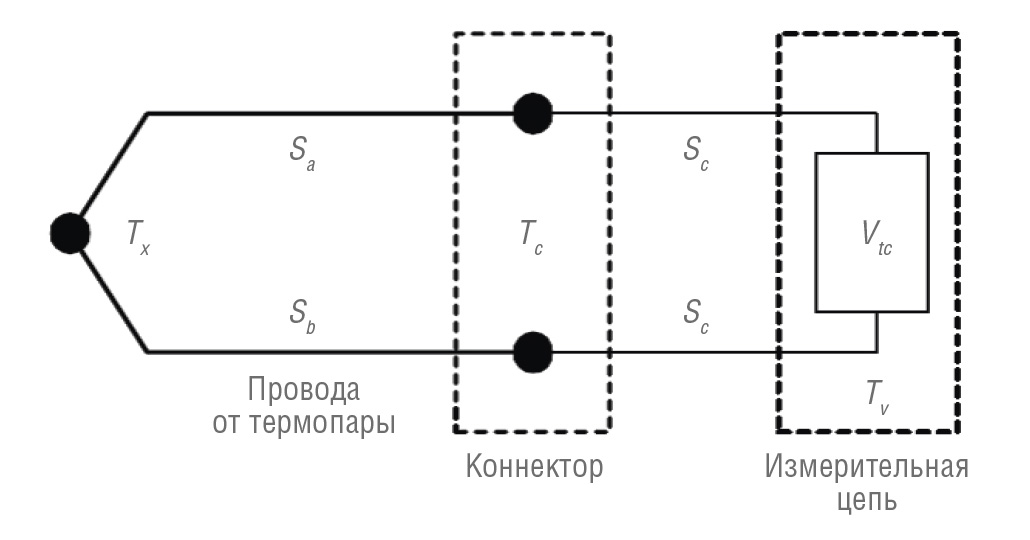
Условные обозначения:
Tx – измеряемая температура; Tc – температура на разъёме вольтметра (предполагается одинаковой для обоих проводов); Tv – внутренняя температура всех элементов цепи вольтметра; Sa – коэффициент Зеебека материала термопары а; Sb – коэффициент Зеебека материала термопары b; Sc – коэффициент Зеебека проводников, используемых в цепи измерения напряжения; VTC – напряжение разомкнутой цепи термопары. Измерительная цепь измеряет VTC. Чтобы минимизировать ток контура, цепь имеет высокий импеданс.
Вспомним правило напряжений (второе правило) Кирхгофа, которое гласит, что при отсутствии в замкнутом контуре источника ЭДС алгебраическая сумма напряжений на его резистивных элементах равна нулю. Применение формулы (1) для контура этой цепи даёт:
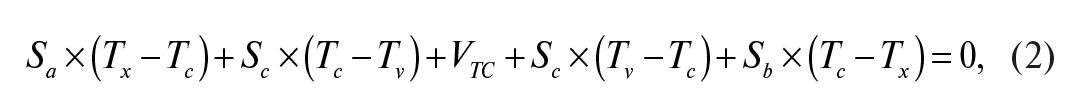
где Tx – измеряемая температура; Tc – температура на разъёме вольтметра; Tv – внутренняя температура всех элементов цепи вольтметра; Sb – коэффициент Зеебека материала термопары b; Sc – коэффициент Зеебека проводников, используемых в цепи измерения напряжения; VTC – напряжение разомкнутой цепи термопары.
Или в упрощённом виде:

Значения Sa и Sb определяют полярность VTC (Sa – Sb) = Sab и (Sb – Sa) = –Sab. Эти термины определены отраслевыми стандартами как коэффициент Зеебека Sab, обозначающий термопару типа ab, изготовленную из материалов a и b.
Из формулы (3) вытекают следующие важные характеристики поведения термопары.
- Действие термопары из двух различных материалов (эффект Зеебека) – это физическое явление, зависящее исключительно от внутренней молекулярной структуры материала и не зависящее от типа соединения между материалами: соединение просто должно обладать хорошим электрическим контактом.
- Термопары измеряют разницу температур между концом соединения и открытым концом, но вовсе не абсолютную температуру на спае.
- Оба провода термопары на соединении со схемой измерения напряжения создают нежелательные соединения термопары между разъёмом при температуре Tc и проводами цепи вольтметра при температуре Tv. Если эти паразитные соединения имеют температуру Tc и если все элементы в цепи вольтметра имеют температуру Tv, то действие этих паразитных соединений взаимно компенсируется. Данное условие становится обязательным требованием для использования термопар.
- Напряжения термопары должны измеряться с помощью цепей с максимально высоким полным сопротивлением, чтобы ток измерительного контура был близок к нулю. Протекание тока в термопарах может создавать ошибки, нарушая тепловое распределение электронов.
Формула (3) является основным рабочим уравнением для измерения температуры с помощью термопар. Учитывая Sab и температуру Tc, можно определить неизвестную температуру Tx. Схема подключения термопары, показанная на рис. 3, представляет собой основу для определения стандартных таблиц термопар. В схему добавляется дополнительный спай, удерживаемый в ледяной бане при температуре плавления льда Tice (0°C/32°F).
Разработчики стандартов и производители термопар используют эту топологию для создания таблиц зависимости напряжения термопары от температуры.
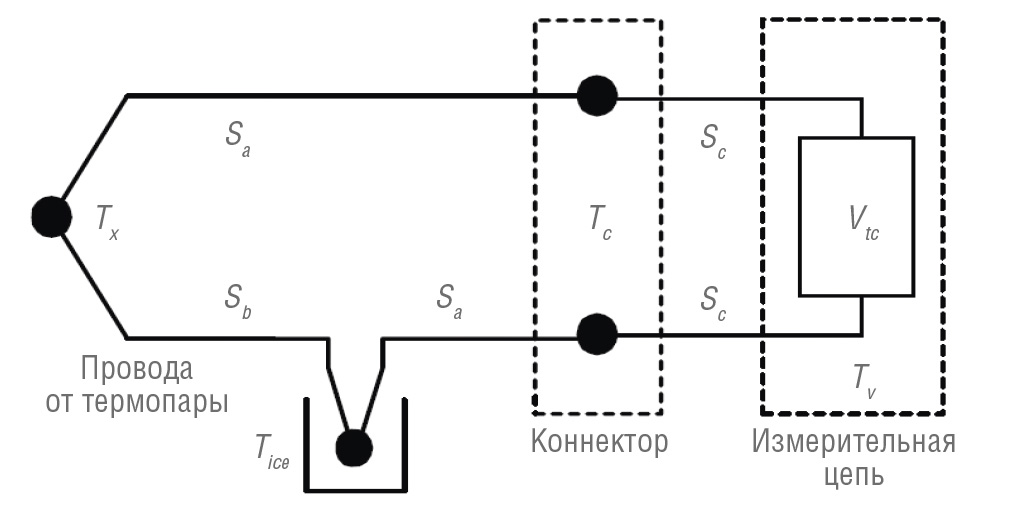
Условные обозначения:
Tx – измеряемая температура; Tc– температура на разъёме вольтметра (предполагается одинаковой для обоих проводов); Tv– внутренняя температура всех элементов цепи вольтметра; Sa – коэффициент Зеебека материала термопары а; Sb – коэффициент Зеебека материала термопары b; Sc– коэффициент Зеебека проводников, используемых в цепи измерения напряжения; VTC– напряжение разомкнутой цепи термопары; Tice– температура плавления льда.
Анализ схемы на рис. 3 с помощью формулы (1) и методики, использованной для вывода формул (2) и (3), даёт:
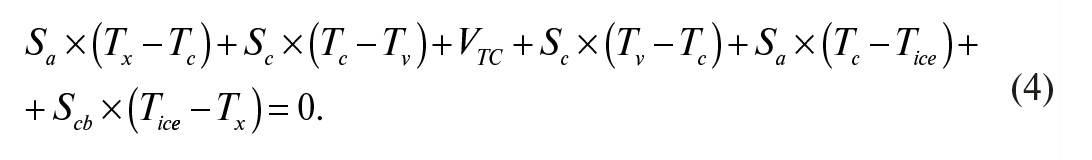
Или в упрощённом виде:

Важное замечание: из формулы (5) исключены как температура разъёма Tc, так и температура цепи измерения напряжения Tv. Температура ледяной бани Tice фиксирована; следовательно, неизвестная температура Tx всегда может быть определена путём измерения напряжения VTC по любой соответствующей таблице поиска термопары (на основе эталонной точки плавления льда).
Эта методика измерения температуры при помощи термопары была разработана примерно в 1828 году. С тех пор материалы, таблицы и аналитические модели термопар прошли путь совершенствования длиной более 170 лет и стали очень эффективной системой измерения температуры.
Современные модули формирования сигнала используют полупроводниковую электронику, которая устраняет неуклюжие ледяные ванны, электронно моделируя температуру точки плавления льда эталонного спая. Этот процесс называется компенсацией холодного спая (CJC – Cold Junction Compensation). Кроме того, современные модули формирования сигнала линеаризуют нелинейное поведение коэффициентов Зеебека и обеспечивают линейные масштабированные выходные данные в вольтах или амперах на °С. О методах реализации CJC и линеаризации сигнала термопар будет рассказано далее.
Типы термопар
Как мы увидели, термопары стали стандартом в отрасли как экономически эффективный метод измерения температуры. Со времени их изобретения Томасом Иоганном Зеебеком в 1821 году на предмет использования в термопарах были исследованы термоэлектрические свойства множества различных материалов. Исследователи, применяя достижения современной металлургии, разработали специальные пары материалов, оптимальные для использования в качестве датчиков термопар.
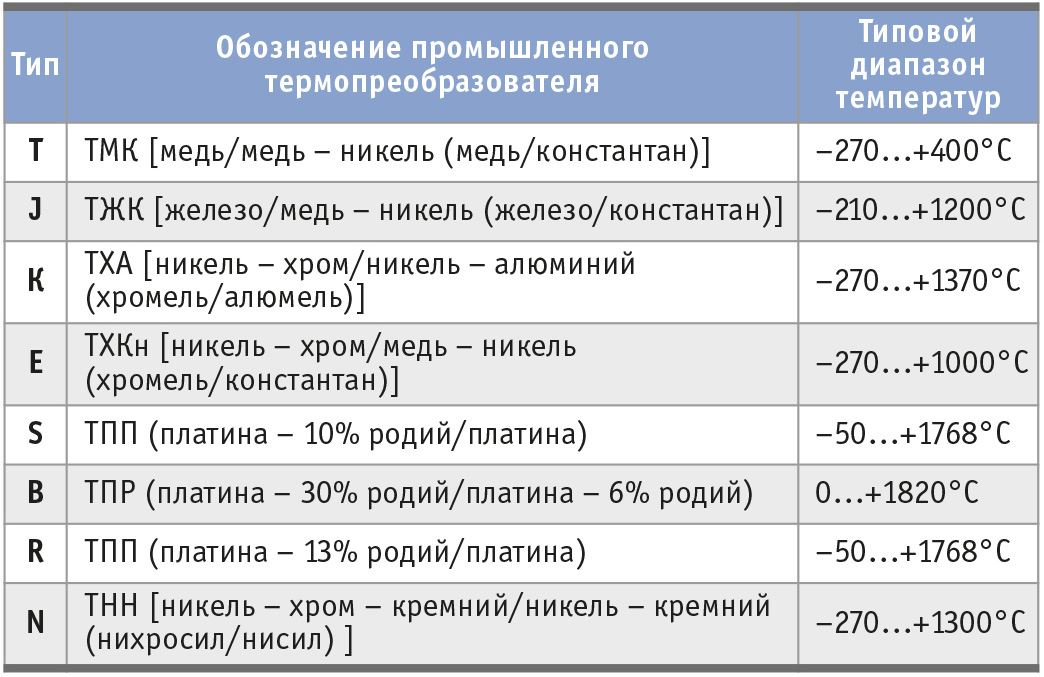
В табл. 1 представлены восемь стандартных термопар, популярных в промышленности, и их типичные характеристики. Буквы в таблице обозначают зависимость температуры от напряжения, а не конкретный химический состав. Производители могут изготовить термопары данного типа с изменениями в составе, однако результирующие зависимости температуры от напряжения должны соответствовать стандартам термоэлектрического напряжения, связанным с конкретным типом термопары.
Полные наборы таблиц температуры и напряжения с привязкой к 0°C, включая математические модели для всех популярных промышленных термопар, доступны на сайте NIST (Национального института стандартов и технологий США), откуда их можно бесплатно скачать. В России аналогичные таблицы содержит ГОСТ Р 8.585-2001.
Параметры термопар типа L и U регламентируются стандартом DIN 43710; однако они не так часто используются в новых установках, как более популярные стандарты термопар типов T и J. Термопара типа U похожа на популярный стандартный тип T, а термопара типа L аналогична популярному стандарту типа J.
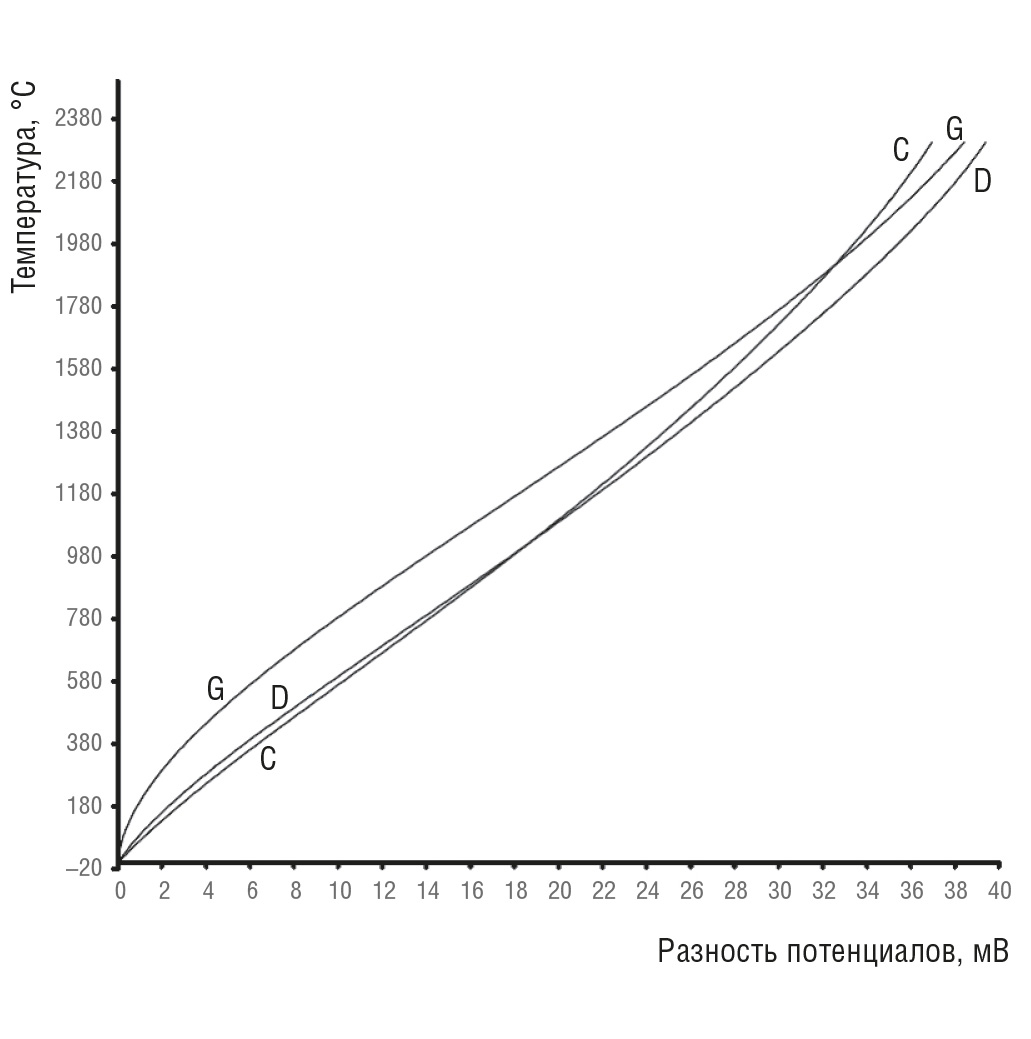
Для измерений высоких температур используются три дополнительных типа термопар: C, D и G. Их буквенные обозначения (C, D, G) не признаны стандартами ANSI, тем не менее такие термопары тоже доступны. Применяемые в них композиции материалов следующие:
- тип G: W и W – 26% Re,
- тип C: W – 5% Re и W – 26% Re,
- тип D: W – 5% Re и W – 25% Re,
где W – вольфрам, Re – рений.
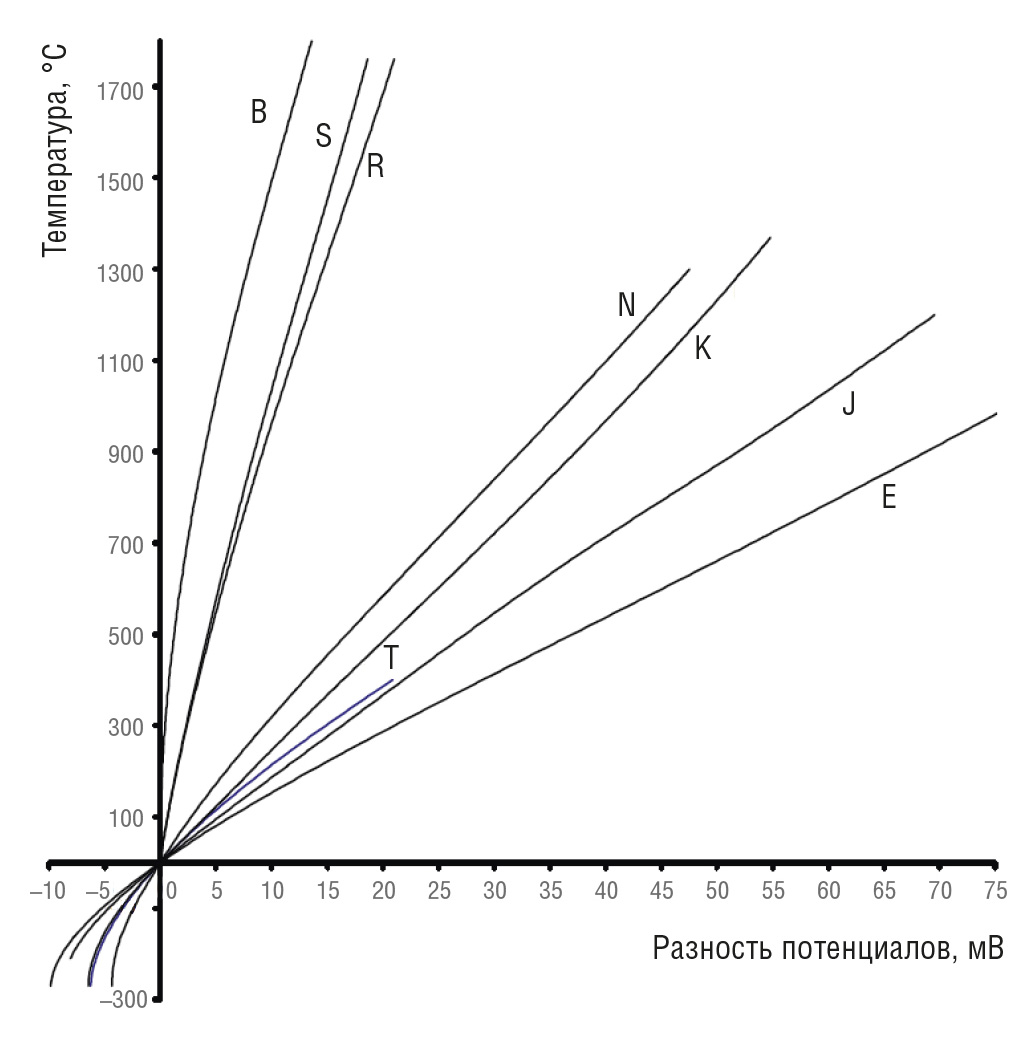
Таким образом, с помощью термопар, несмотря на то что их выходное напряжение составляет милливольты, а чувствительность – микровольты на °С, да ещё при нелинейных характеристиках, могут быть довольно точно измерены температуры практически во всех диапазонах. На рис. 4 и 5 представлены типичные характеристики напряжения и температуры для указанных термопар. Эти кривые обеспечивают визуальное представление диапазонов термопар, масштабных коэффициентов, чувствительности и линейности.
Компания Dataforth предлагает модули ввода для термопар, которые взаимодействуют со всеми указанными их типами. Для получения более подробной информации об этих и других современных модулях посетите веб-сайт Dataforth.
Математическая модель термопары
Для каждого типа термопар были разработаны стандартные математические модели в виде степенны́х рядов. Эти модели используют уникальные наборы коэффициентов, различных для разных температурных сегментов и типов термопар. Если не указано иное, все стандартные модели и таблицы термопар имеют привязку к 0°C. Формула (6) иллюстрирует модель степенно́го ряда, используемую для описания всех термопар, кроме типа K, модель которой иллюстрируется формулой (8).

где T – температура, °C.
Набор коэффициентов Ci, используемых в формуле (6) для описания модели термопары типа E для трёх значащих цифр, показан в табл. 2.
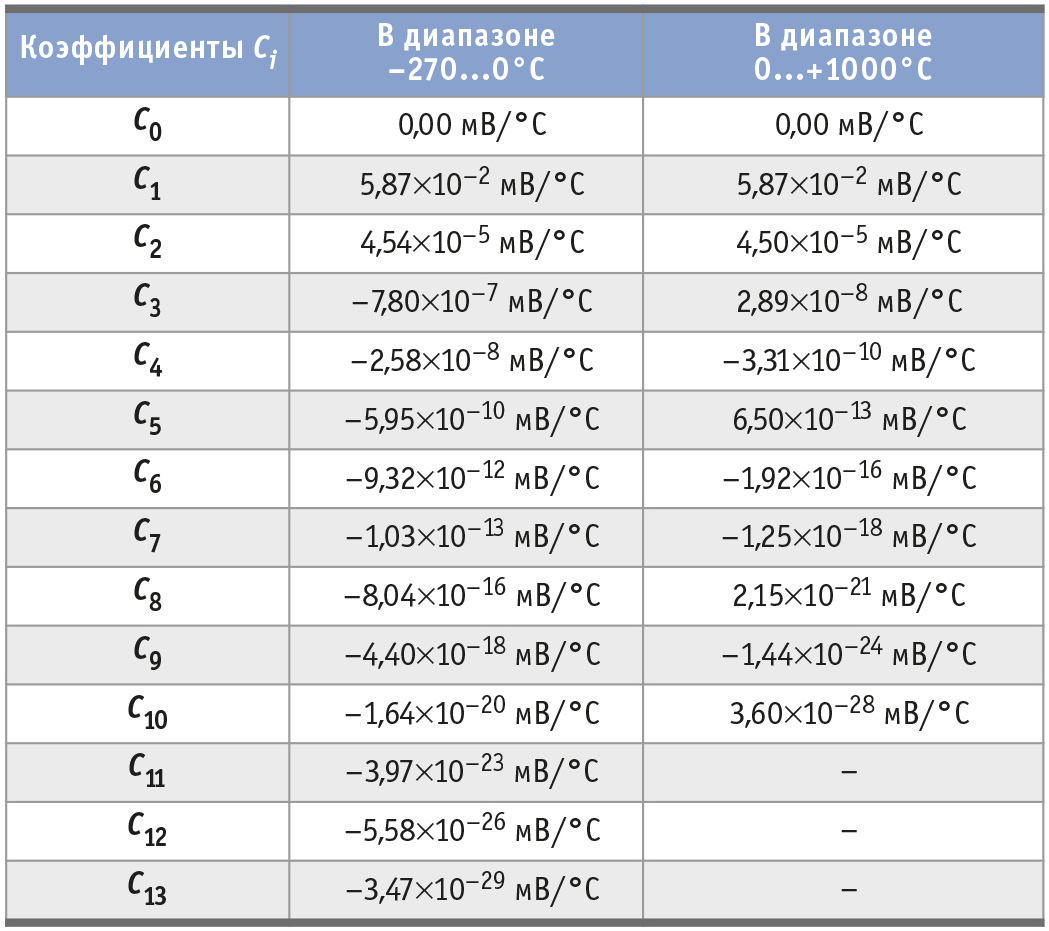
Но когда известно только измеренное напряжение термопары VTC, эти уравнения с различными наборами коэффициентов трудно использовать для непосредственного определения фактических температур, поэтому были разработаны обратные модели для определения температуры по измеренным напряжениям термопары. Уравнение (7) представляет обратную модель:

где VTC – напряжение в мВ.
Набор обратных коэффициентов Di для термопар типа E показан для шести значащих цифр в табл. 3.
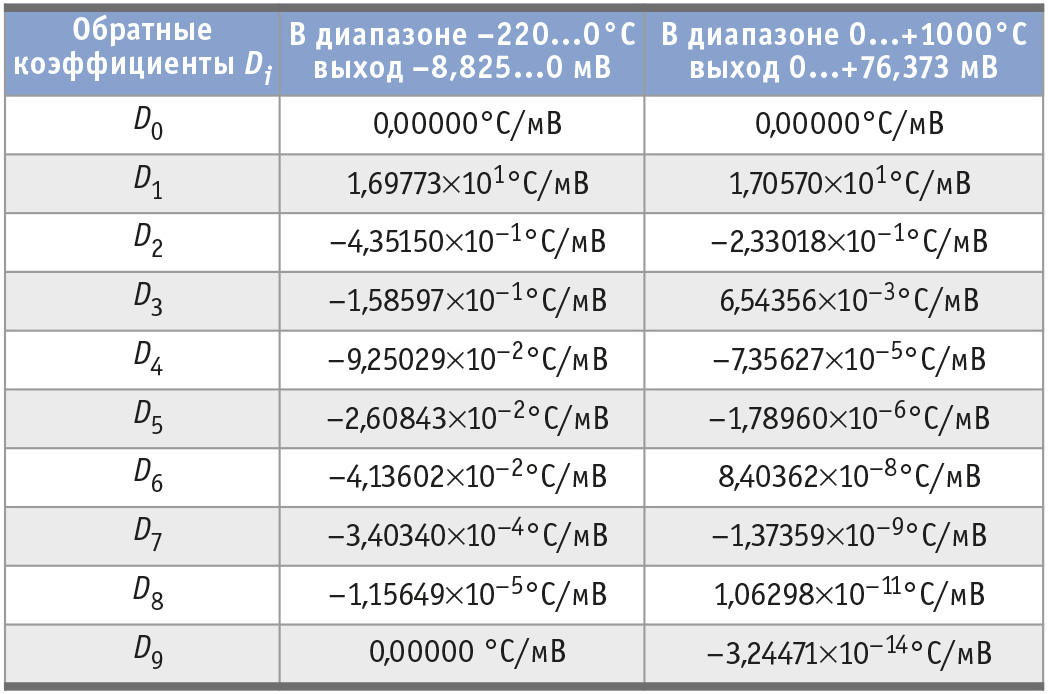
Как было сказано, для термопар типа K требуется другая математическая модель, представленная формулой (8):
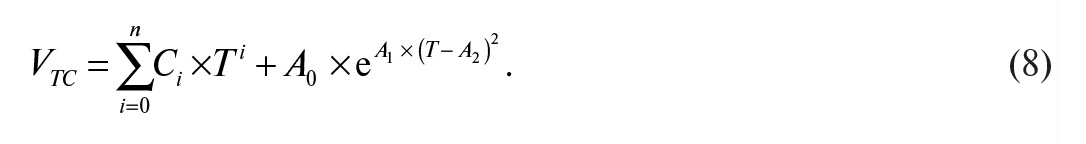
Экспоненциальная часть формулы (8) добавлена для описания особых эффектов, возникающих в термопарах типа K, где A0, A1, A2 – справочные полиномиальные коэффициенты.
Компенсация холодного спая
Стандартные справочные таблицы и модели термопар имеют привязку к нулевой температуре спая, в то время как полевые измерения выполняются термопарой, подключённой к разъёму, температура которого отлична от 0°C. Следовательно, фактическое измеренное напряжение должно быть скорректировано таким образом, чтобы оно отображалось относительно 0°C. Современные модули формирования сигнала разрешают эту ситуацию электронным образом и, кроме того, линеаризуют выходное напряжение термопары. Эти кондиционирующие модули обеспечивают конечному пользователю линейный выходной сигнал, масштабируемый до вольт или ампер на °C (°F). Концепция электронной привязки измерений термопары к 0°C показана на рис. 6. Этот метод известен как компенсация холодного спая, или CJC.
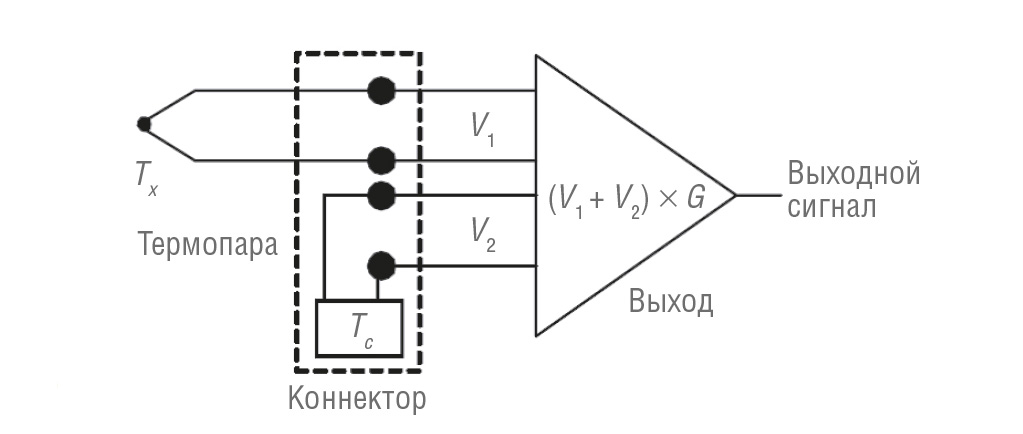
Условные обозначения:
Tx – измеряемая температура; Tc – температура на разъёме вольтметра (предполагается одинаковой для обоих проводов); V1 – напряжение термопары Зеебека; V2 – напряжение датчика; G – коэффициент усиления усилителя.
На рис. 6 напряжение V1 представляет собой напряжение термопары Зеебека, генерируемое разностью между неизвестной температурой Tx и температурой разъёма Tc, как показано в формуле (9):

Температура разъёма Tc измеряется датчиком, работающим не на эффекте термопары (диод, RTD-диод и т.п.), и соответствующее напряжение датчика V2 масштабируется электронным способом для представления того же напряжения термопары Зеебека (относительно 0°C), которое термопара считала бы при использовании для измерения Tc, как показано в формуле (10):

Это приведённое V2 соответствует термопаре того же типа, что и для измерения Tx.
Формула (9) может быть математически преобразована для учёта температуры точки плавления льда Tice:
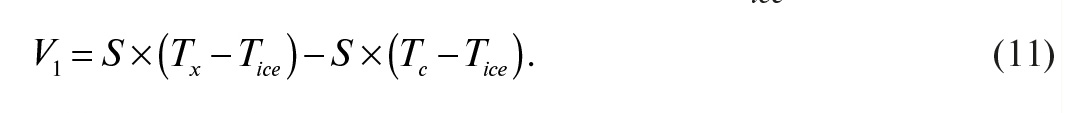
Формула (11) показывает, что напряжение термопары V1 складывается из двух частей, каждая из которых зависит от Tice. Компонент S × (Tx – Tice) является стандартным значением справочной таблицы, необходимым для определения искомой температуры Tx. Компонент S × (Tc – Tice) представляет собой напряжение, полученное, если бы температуру соединителя Tc измеряли с помощью термопары того же типа, что и для измерения Tx. Напомним, что V2 было масштабировано электронным способом, так что V2 равно этому напряжению: V2 = S × (Tc – Tice).
На рис. 6, если коэффициент усиления G = 1, то
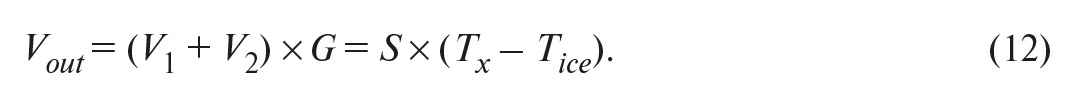
Выходное напряжение Vout в формуле (12) может быть введено непосредственно в справочную таблицу термопар соответствующего типа для определения измеренной температуры.
Линеаризация
Для точных измерений при помощи термопары необходимы модули формирования сигнала с линейно масштабируемыми выходами. Выходные напряжения модуля, которые имеют линейные масштабные коэффициенты в вольтах или амперах на °C, устраняют необходимость в применении справочных таблиц или в дополнительной обработке. Такие модули преобразования сигналов термопары, включая изоляцию и CJC, доступны в номенклатуре изделий Dataforth.
На рис. 4 и 5 показаны зависимости между напряжением и температурой для наиболее распространённых термопар. Эти кривые представлены здесь для визуальной оценки стандартных рабочих диапазонов термопар, величин выходных напряжений, нелинейности и чувствительности (мВ/°C). Хотя диапазоны рабочих температур, в которых могут использоваться термопары, довольно велики, их чувствительность мала и находится в диапазоне мкВ/°C. Кроме того, из рис. 4 видно, что при отрицательных температурах отклик термопары очень нелинейный, однако эти кривые выглядят почти линейными для определённых диапазонов положительных температур. Тем не менее факт остаётся фактом: термопары являются нелинейными.
В качестве примера нелинейности приведём рис. 7. Он иллюстрирует нелинейность термопары, показывая разницу между идеальным линейным откликом и откликом термопары типа J в диапазоне 0…+150°C.
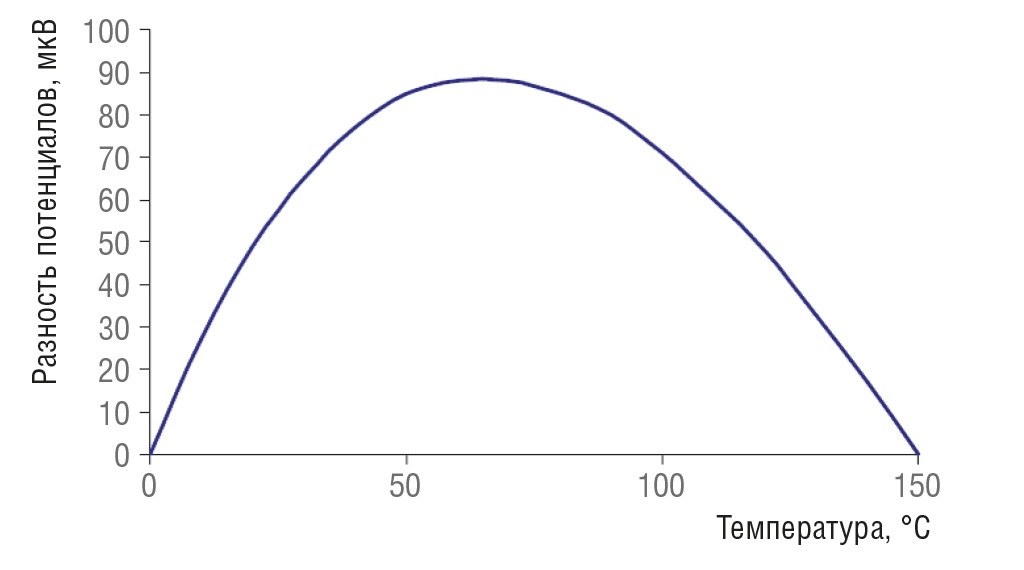
Чувствительность термопары типа J составляет примерно 54 мкВ/°C. Из рис. 7 видно, что игнорирование нелинейности в отклике для термопар типа J может привести почти к двум градусам погрешности.
Итак, для обеспечения точных измерений температуры с помощью термопар становится очевидной необходимость линеаризации. Компания Dataforth разработала и запатентовала схемы, которые обеспечивают точную линеаризацию для модулей преобразования сигналов. Хотя современные ПК или другие встраиваемые микропроцессоры могут линеаризовать сигнал термопары с помощью программных методов, аппаратная линеаризация обеспечивает более быстрые результаты и не потребляет ценные компьютерные ресурсы.
Для достижения линейности коэффициент усиления G на рис. 6 и в формуле (12) внутренне запрограммирован для выборочного масштабирования функции напряжения S × (Tx – Tice) таким образом, чтобы она стала линейной.
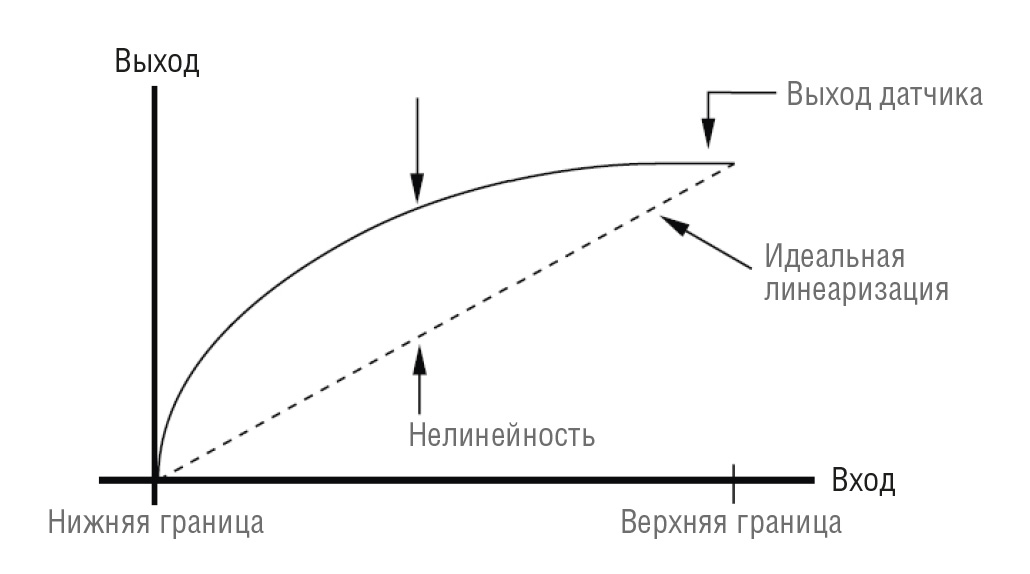
Многие датчики, используемые в промышленности, демонстрируют отклонение от идеальной (линейной) связи между входом и выходом. Датчики или сигналы, имеющие такое поведение, называются нелинейными. Гипотетическая нелинейная передаточная функция показана на рис. 8. Некоторые из модулей серии SCM5B (рис. 9) имеют возможность формирования нелинейной передаточной функции средствами самого модуля.

Эта функция нелинейного преобразования настраивается на заводе и предназначена для зеркальной компенсации равных и противоположных по значению нелинейностей характеристик датчика. В результате выходной сигнал модуля является линейным по отношению к данному входному значению температуры. Выходной сигнал SCM5B, линеаризованный аппаратными средствами, удобен для клиента, поскольку устраняет необходимость в программной компенсации, создающей линеаризованный сигнал с помощью полиномов высокого порядка или справочных таблиц. Для исправления нелинейности сигнала в модулях SCM5B используется аппаратная техника кусочно-линейной аппроксимации. Разница между нелинейностью датчика и результатом линеаризации, обеспечиваемой модулем SCM5B, называется ошибкой соответствия. Этот параметр является мерой того, насколько хорошо техника линеаризации соответствует нелинейной кривой. Точки перегиба расположены вдоль кривой так, чтобы выровнять ошибки положительного и отрицательного несоответствия. Для исправления нелинейности модули SCM5B используют 9 точек перегиба (кривая разбивается на 10 сегментов), что позволяет добиться типичного соответствия в пределах ±0,015% во всем диапазоне. Нормализованный график нелинейности датчика и аппаратной линеаризации показан на рис. 10.
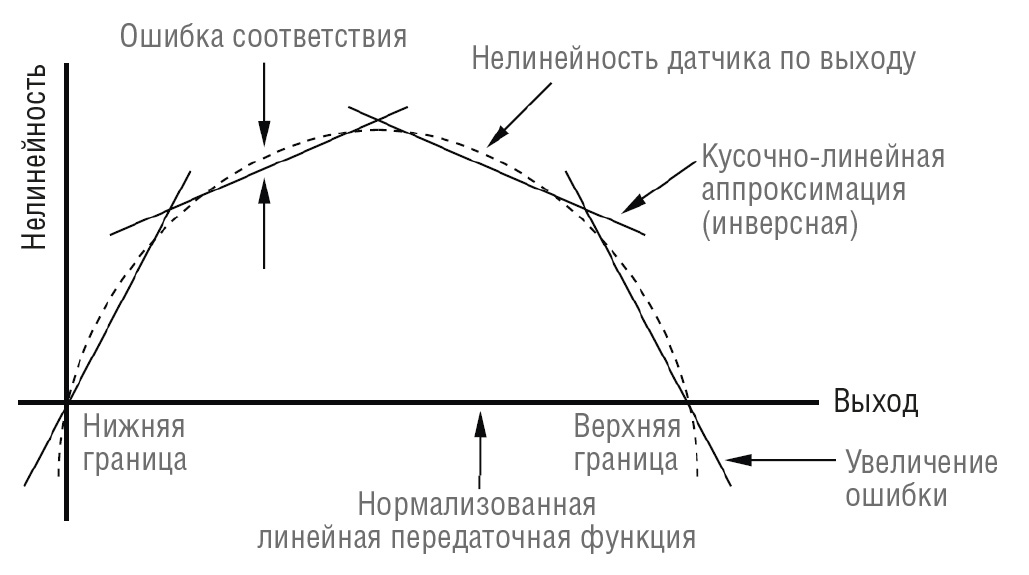
Линеаризация сигнала гарантируется в пределах заявленного минимума и максимума входного сигнала. Для любого значения в этих пределах выход модуля будет линейным, но если входной сигнал превышает минимальное или максимальное значение, линейность выходного сигнала модуля не гарантируется. Это также показано на рис. 10. По этой причине работа модуля SCM5B за пределами указанного входа не рекомендуется.
Практические соображения
Далее приведены полезные советы, которые следует учитывать при измерении температуры с помощью термопар.
- Всегда проверяйте спецификации производителей термопар на соответствие стандартам, указанным температурным диапазонам и взаимозаменяемости.
- Следует изучить воспроизводимость и взаимозаменяемость между марками термопар. Нужно избегать ошибок, возникающих из-за замены термопары.
- Чтобы избежать возникновения контуров заземления, используйте изолированные модули формирования сигнала.
- Всегда используйте модули формирования сигнала термопары с соответствующей входной фильтрацией. Это поможет избежать серьёзных шумовых ошибок.
- Все провода термопары, подключённые к сенсорному модулю, должны иметь одинаковую температуру. Разъёмы модуля не должны иметь температурных градиентов между отдельными соединениями.
- Поведение термопары зависит от молекулярной структуры материалов. Условия окружающей среды, такие как механические деформации, химическая коррозия, радиация и т.д., которые влияют на молекулярную структуру в любом месте по длине провода термопары, могут привносить ошибки. Например, термопары с железом в их составе подвержены ржавлению, что может привести к ошибкам.
- Используйте удлинительные провода для витой пары и модули формирования сигнала с соответствующей фильтрацией, чтобы избежать ошибок EMI (Electromagnetic Interference – электромагнитные помехи) и RFI (Radio Frequency Interference – радиочастотные помехи).
- Делайте соединительные провода термопары по возможности короткими.
- Если необходимы длинные провода термопары, используйте удлинители, рекомендованные производителем.
- Всегда соблюдайте полярность цветового кода: некоторые европейские производители, в отличие от североамериканских, используют противоположные цвета для маркировки положительной и отрицательной полярности.
- Избегайте тепловых помех при установке термопар. Любой теплопроводящий материал, например массивные свинцовые провода, может отводить тепло от термопары, создавая ошибку.
- Агрессивные среды в сочетании с влагой и теплом могут вызвать коррозию, которая способна стимулировать гальваническое воздействие и создавать электрохимические ошибки напряжения.
- Напомним, что на время отклика термопары существенно влияет время отклика контура измерения температуры. Например, установленные в термальном колодце термопары имеют медленное время отклика, что может вызвать нежелательное рассогласование в контуре управления.
- Некоторые термопары доступны в конструктивах с соединением с корпусом. Это заземлённые термопары, которые могут вызвать проблемы с контуром заземления. Рассматривайте использование изолированных модулей, чтобы избежать таких проблем.
- Убедитесь, что в модулях формирования сигнала с электронными методами CJC используются чувствительные к температуре устройства, у которых время теплового отклика равно времени измерения используемых термопар.
Ещё немного о модулях Dataforth SCM5B
Dataforth предлагает полную линейку модулей для всех типов термопар. Эти модули обеспечивают отличную изоляцию, превосходную точность и линейность. На рис. 11 показана функциональная блок-схема модуля изолированной линеаризованной термопары Dataforth SCM5B47. Каждый входной модуль термопары SCM5B47 имеет один канал ввода термопары, который фильтруется, изолируется, усиливается, линеаризуется и преобразуется в аналоговый выход высокого напряжения. Этот выход напряжения управляется логическим переключателем, что позволяет модулям использовать общую аналоговую шину без необходимости применения внешних мультиплексоров.
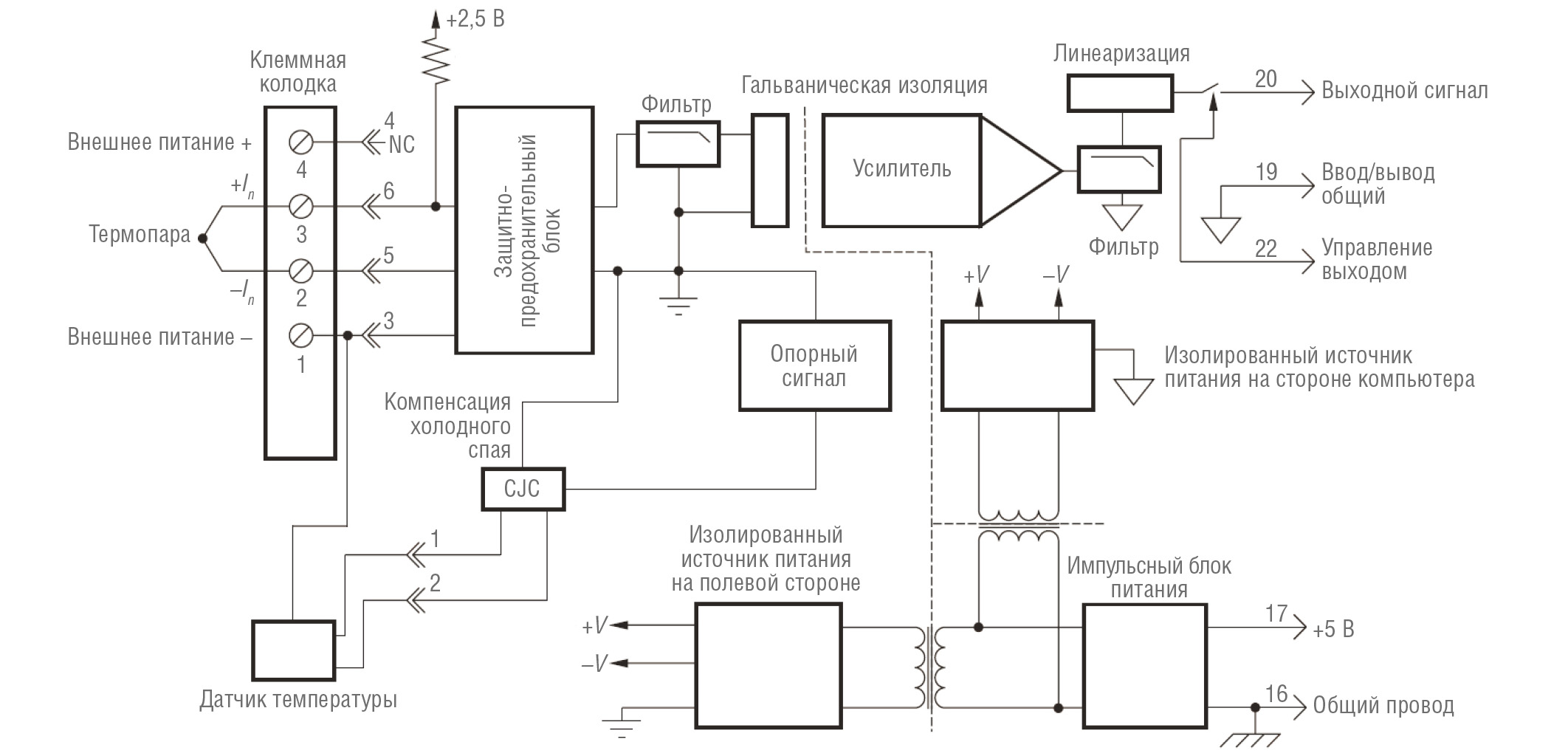
Условное обозначение: NC – свободный вывод.
Модули SCM5B спроектированы с полностью изолированной схемой на стороне компьютера, которая может быть подключена к ±50 В от общего источника питания, вывод 16. Такая полная изоляция означает, что для правильной работы выхода не требуется никакого соединения между общим входом/выходом и общим питанием. Этот модуль может взаимодействовать с восемью типами промышленных термопар: J, K, T, E, R, S, N и B. Его выходной сигнал линеен в диапазоне 0…+5 В. Модуль имеет компенсацию холодного спая для коррекции паразитных термопар, образованных проводом термопары и винтовыми клеммами на монтажной задней панели. Эффективное обнаружение обрыва термопары обеспечивается внутренним подтягивающим резистором. Индикация обрыва может быть реализована путём установки внешнего резистора между винтовыми клеммами 1 и 3 на задних панелях SCMPB01/02/03/04/05/06/07.
Фильтрация сигнала осуществляется с помощью шестиполюсного фильтра, который обеспечивает подавление помех в нормальном режиме на уровне 95 дБ при 60 Гц и на уровне 90 дБ при 50 Гц. Два полюса этого фильтра находятся на полевой стороне изолирующего барьера, а остальные четыре – на стороне компьютера. После начальной фильтрации на полевой стороне входной сигнал развязывается от выхода запатентованной цепью. Изоляция обеспечивается с помощью трансформаторной развязки, с использованием запатентованной технологии подавления передачи синфазных пиков и скачков напряжения. Модуль питается от +5 В постоянного тока ±5%. Специальная входная цепь модулей SCM5B47 обеспечивает защиту от случайного подключения напряжений линии питания до 240 В переменного тока.
Заключение
Такая, казалось бы, простая и знакомая любому инженеру вещь, как термопара, прошла в своём развитии путь длиной почти в 200 лет. В основе точных измерений температуры сегодня лежат достаточно сложная физическая теория, математический аппарат, а также достижения современной электроники и вычислительной техники. В качестве примера практического воплощения мы привели изделия компании Dataforth, с 1984 года являющейся экспертом в области промышленных средств сбора и передачи данных, а также формирования сигналов. Если ваша система автоматизации потребует подобной функциональности, смело обращайтесь к продуктам Dataforth – эталону надёжности и промышленного качества.
Статья подготовлена на основе материалов компании Dataforth
E-mail: textoed@gmail.com
Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!