Классические измерения значений напряжения (тока) основаны на понятиях «среднее» и «эффективное». Для усреднения значения функции напряжения V во времени берётся чистая площадь функции, рассчитанная за определённый интервал времени, и делится на этот временно́й интервал:

Причём если значение напряжения (тока) является постоянной или периодической величиной, то его среднее значение не зависит от интервала, в течение которого производится измерение. С другой стороны, если функция напряжения (тока) растёт без ограничения во времени, среднее значение зависит от интервала измерения и не обязательно будет постоянным, то есть никакого среднего значения в данном случае не существует. К счастью, на практике в мире электротехники значения напряжений и токов не растут безгранично и, следовательно, имеют определимые средние значения. Это является следствием того факта, что источниками реального напряжения (тока), как правило, являются либо батареи с постоянными или медленно (экспоненциально) затухающими значениями токов/напряжений, либо генераторы, имеющие на выходе сигналы в виде ограниченных синусоидальных функций времени, либо сочетания перечисленного. Синусоидальные функции с постоянной амплитудой имеют чистое нулевое среднее значение за интервалы времени, кратные их периоду. Более того, их средние значения могут быть рассчитаны за бесконечное число интервалов, не равных периоду синусоиды. Эти средние значения также будут равны нулю. Но хотя среднее значение ограниченной синусоидальной функции равно нулю, её так называемое эффективное значение нулю не равно. В качестве примера приведём электрические водонагреватели, которые прекрасно работают, будучи запитанными от сети переменного тока с синусоидальным напряжением с нулевыми средними значениями.
Эффективное значение
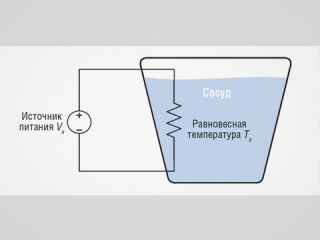
Эффективное значение симметричных периодических функций напряжения (тока) от времени основано на понятии «нагревательная способность». Рассмотрим тестовую установку, показанную на рис. 1.
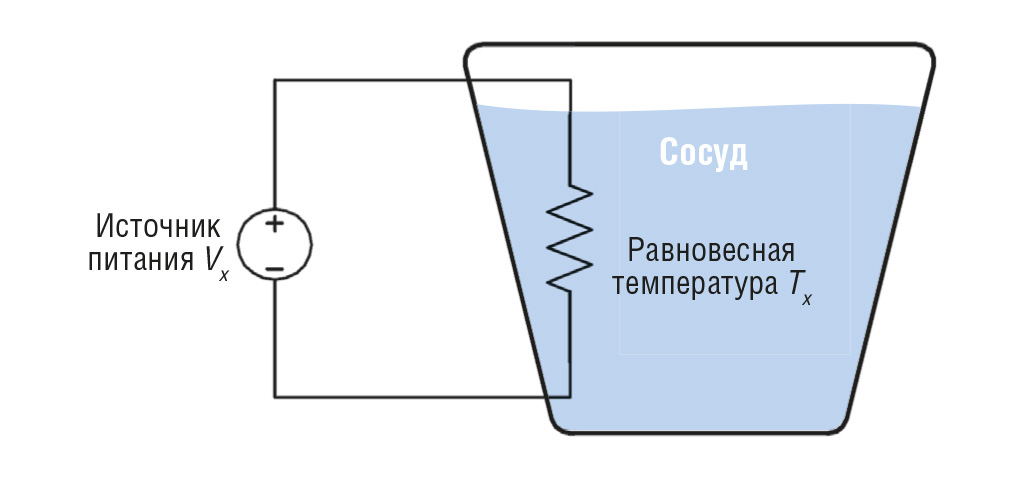
Сосуд на рисунке изолирован и заполнен некоторой стабильной жидкостью (например, трансформаторным маслом), способной достичь термодинамического равновесия. Если на внутренний нагреватель сосуда подать ток постоянного напряжения Vx, температура жидкости станет подниматься. В какой-то момент будет достигнуто состояние, при котором электрическая энергия, подаваемая на нагреватель в этом сосуде, будет равна потере энергии (тепла), и жидкость сосуда приобретёт равновесную температуру Tx градусов.
Заменим в этом экспериментальном сценарии источник постоянного напряжения Vx на источник с периодически изменяющимся во времени напряжением. Тогда через некоторое время Tfinal снова будет достигнуто тепловое равновесие. Если это условие равновесия устанавливает ту же температуру Tx, которая была достигнута ранее с приложенным напряжением постоянного тока Vx, то можно сказать, что эффективное значение этой изменяющейся во времени функции равно Vx.
Отсюда и определение эффективного значения, которое иллюстрирует формула (2):
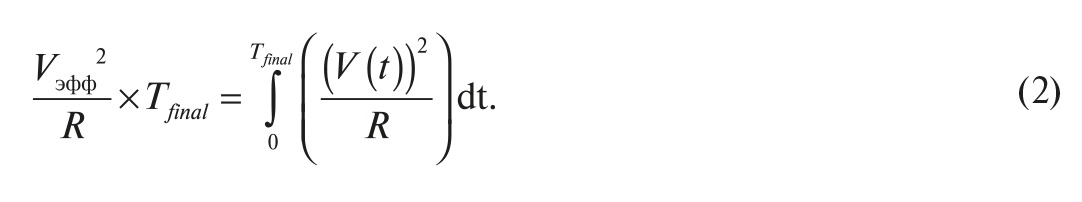
Здесь R – сопротивление. Если V(t) – периодическая функция времени с периодом Tp, а Tfinal – целое число, умноженное на период (n × Tp), то интеграл по Tfinal будет просто n-кратным интегралом по Tp. Результаты применения этих соображений приведены в формуле (3):

Формула (3) показывает, что эффективная эквивалентная теплопроизводительность ограниченной периодической функции напряжения (тока) может быть определена за один период. Это уравнение и есть представление действующего, или среднеквадратического значения электрического тока (Root Mean Square). Отсюда и происходит общеизвестная аббревиатура RMS.
Примеры использования формулы RMS
Прямое применение формулы (3) для распространённых случаев даёт следующие результаты.
.jpg)
Примечание. Приведённые примеры иллюстрируют, что среднеквадратическое значение определяется формой периодической функции. Для вычисления среднеквадратического значения часто ошибочно используется значение пика (гребня) функции напряжения (тока) во времени, делённое на 2. Этот метод может привести к ошибкам, и его определённо следует избегать.
Эффективные значения сложных функций
Чрезвычайно полезным для определения среднеквадратических значений фактом является то, что любая ограниченная во времени периодическая функция может быть выражена в виде суммы некоего постоянного значения и набора синусоид, представляющих гармонический спектр сложного колебания (преобразование Фурье).
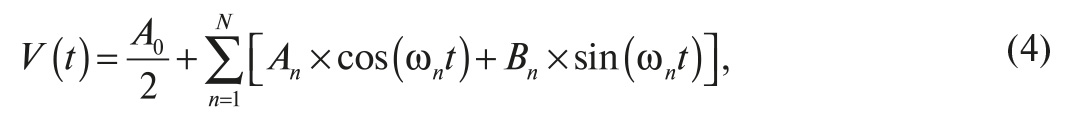
Если этот ряд подставить в интегральное выражение формулы для RMS, получаем следующее:

где Fn – амплитуда n-й гармоники.
Практические соображения
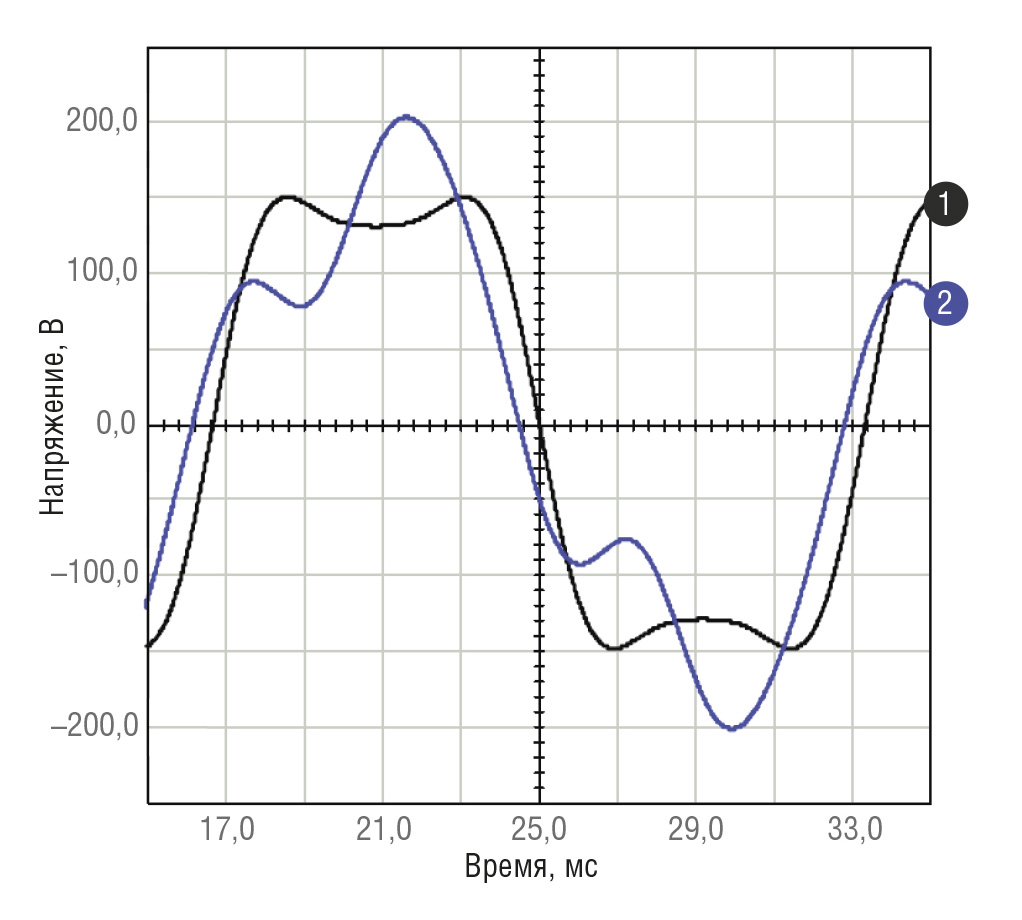
На рис. 2 показаны результирующие кривые, образованные сложением двух синусоид: одной с частотой 60 Гц и второй с частотой 180 Гц. Кривая 1 соответствует нулевому сдвигу фаз между синусоидами, а кривая 2 – сдвигу фаз 90°.
Кривая 1: V(t)=170×sin(377×t)+50×sin(1131×t).
Кривая 2: V(t)=170×sin(377×t)+50×cos(1131×t).
Форма результирующей кривой определяется гармониками фазы и частоты.
В промышленных электросетях часто присутствуют гармоники, влияющие на форму волны и её пиковые значения.Например, кривая 2 типична для токов намагничивания в трансформаторах и двигателях при частоте 60 Гц. В недорогих устройствах для измерения среднеквадратических значений часто используются выпрямители, которые фиксируют пиковое значение, просто умножаемое затем на 0,707 и отображаемое как среднеквадратическое значение. Очевидно, что в некоторых случаях этот метод может дать ошибочные показания RMS. В этом примере использование формулы Vp/√2 явно даёт неверные результаты:
для кривой 1 получаем: 203 × 0,707 = 144 В, что не является истинным среднеквадратическим значением;
для кривой 2 получаем: 155 × 0,707 = 110 В, что также не является истинным среднеквадратическим значением.
.jpg)
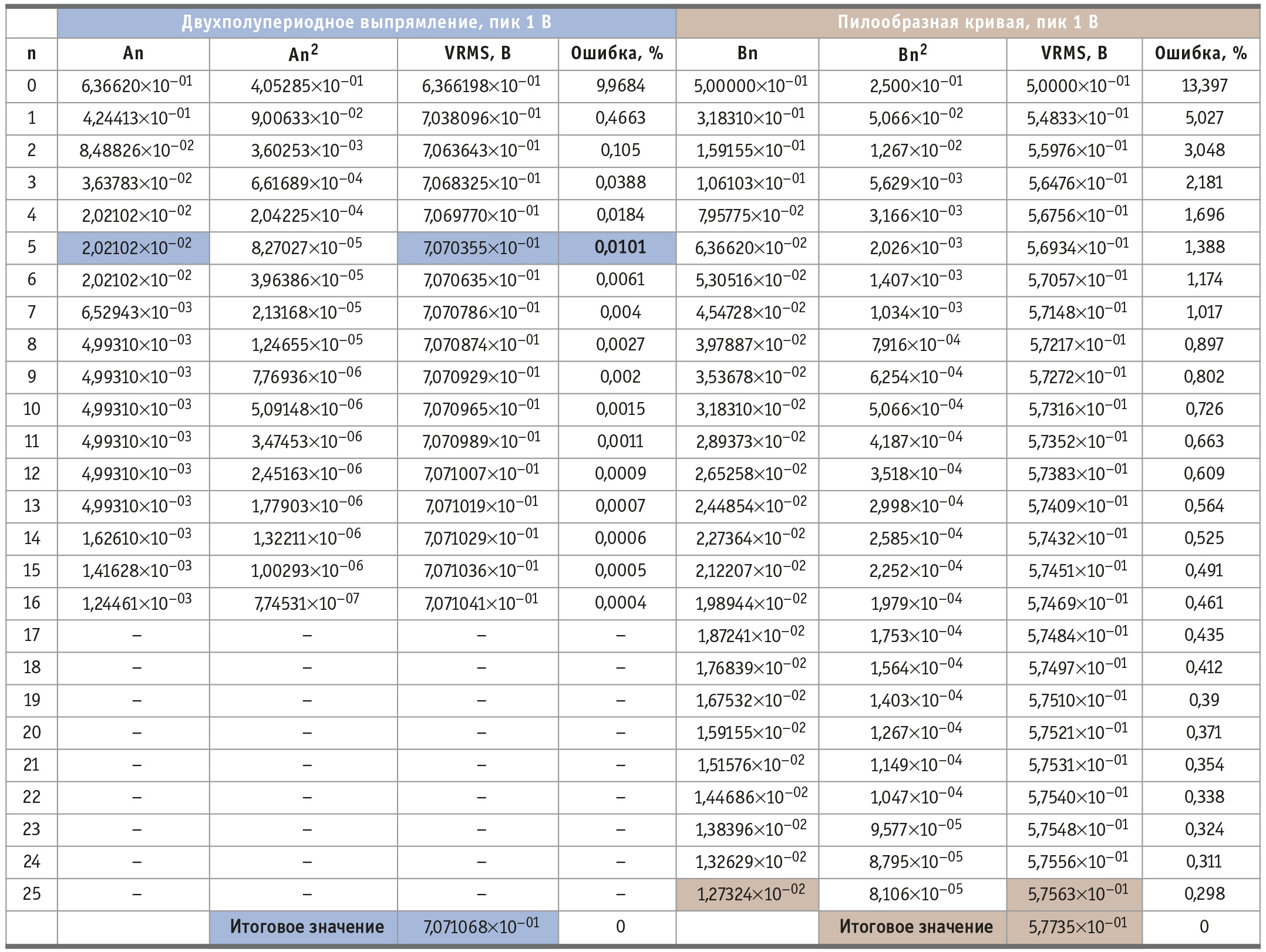
Таблица 1 иллюстрирует два примера вычислений RMS с использованием индивидуальных коэффициентов Фурье и формулы (5). Первым примером является выпрямленная двухполупериодным выпрямителем синусоида с пиком 1 В. Обратите внимание, что для функции двухполупериодного выпрямления измерительному устройству, необходимому для получения показаний RMS с погрешностью 0,01%, требуется полоса пропускания, захватывающая пятую гармонику, и разрешение 10 мВ.
Другой пример, проиллюстрированный таблицей 1, представляет собой пилообразную функцию напряжения 1 В.
В этом примере измерительному устройству, необходимому для получения показаний RMS с погрешностью 0,3%, требуется полоса пропускания, захватывающая двадцать пятую гармонику, и разрешение 10 мВ.
В целях иллюстрации предположим, что пульсации переменного тока на выходе выпрямителя могут быть аппроксимированы пилообразной функцией. В табл. 1 показано, что для измерения среднеквадратических пульсаций переменного тока с пиковыми значениями 10 мВ на выходе выпрямленной синусоиды частотой 20 кГц с погрешностью 0,3% измерительное устройство должно иметь полосу пропускания более 500 кГц и разрешение для фиксации уровней напряжения 40 дБ (100 мкВ). Этот пример ясно показывает, что на точность измерения истинного среднеквадратического значения чрезвычайно сильно влияют форма измеряемого сигнала, ширина полосы пропускания и разрешение.
Любое устройство измерения истинного среднеквадратического значения должно быть способно точно реализовать формулу (3). Тонкость этого утверждения состоит в том, что электронная реализация формулы (3) требует, чтобы устройство имело очень широкую полосу пропускания и было способно распознавать малые измеряемые величины.
Пик-коэффициент
Ещё одним показателем качества источника питания, часто используемым для описания периодической временно́й функции напряжения (тока), является пик-коэффициент, или пик-фактор (Crest Factor – CF). Это показатель, характеризующий способность источника питания питать нелинейную нагрузку, потребляющую импульсный ток. Пик-коэффициент для конкретной формы волны определяется как пиковое значение, делённое на среднеквадратическое значение:

Для ранее приведённых типовых случаев RMS можно вычислить и CF:
- Чистая синусоида: CF=√2
- Меандр: CF = 1.
- Несимметричная периодическая импульсная волна со спадами D: CF=1/√D
- Симметричная периодическая треугольная волна: CF=√3
- Выпрямленная двухполупериодным выпрямителем синусоида: CF=√2
- Выпрямленная однополупериодным выпрямителем синусоида: CF=2.
кривая 1: CF = 1,62;
кривая 2: CF = 1,24.
Измерительные устройства Dataforth RMS

Итак, для качественных измерений среднеквадратических значений требуются измерительные приборы, которые точно реализуют уравнение среднеквадратического значения. Эти устройства должны иметь широкую полосу пропускания и хорошее разрешение для сигналов низкого уровня, что позволяет им поддерживать измерения при высоких значениях пик-коэффициентов. Компания Dataforth разработала два продукта, удовлетворяющих этим требованиям, – True RMS-модули ввода SCM5B33 (рис. 3) и DSCA33 (рис. 4). Оба этих продукта обеспечивают гальваническую изоляцию 1500 В между входом и выходом. SCM5B33 – это съёмный панельный модуль, а DSCA33 – устройство, предназначенное для монтажа на DIN-рейку. Каждый из них обеспечивает один канал входа переменного тока, значение которого преобразуется в истинное среднеквадратическое значение постоянного тока, фильтруется, гальванически развязывается, усиливается и преобразуется в выходной сигнал напряжения или тока.

Модуль SCM5B33
Модуль ввода SCM5B33 True RMS (рис. 5) обеспечивает один канал входа переменного тока, который преобразуется в стандартное выходное напряжение или ток процесса.
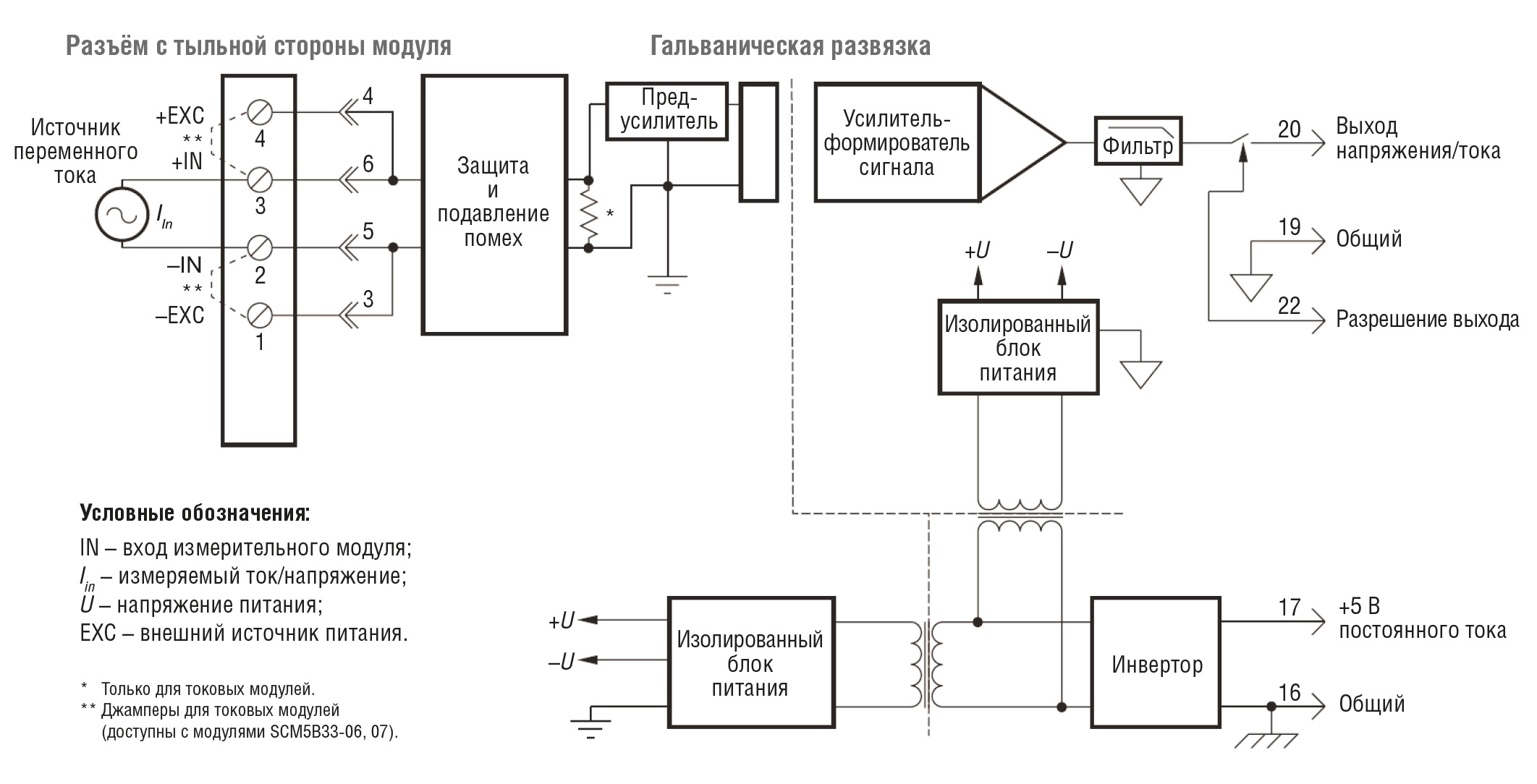
Модули SCM5B содержат полностью изолированную со стороны компьютера цепь, на которую может быть подано до ±50 В относительно общего провода (контакт 16). Эта полная изоляция означает, что для правильной работы выхода не требуется никакого соединения между общим входом/выходом и общим питанием. При желании выход модуля можно сделать включённым постоянно, просто подключив контакт разрешения чтения 22 к общему проводу ввода/вывода (контакт 19).
Входной сигнал напряжения или тока с полевой стороны обрабатывается предварительным усилителем и преобразователем среднеквадратических значений на полевой стороне изолирующего барьера. Преобразованный в постоянный ток сигнал затем гальванически развязывается запатентованной схемой и передаётся через трансформаторный изолирующий барьер, подавляющий передачу синфазных пиков и выбросов. Схема на стороне компьютера восстанавливает сигнал и преобразует его к стандартному выходному уровню. Модули питаются от +5 В постоянного тока ±5%.
Для моделей с токовым выходом требуется внешний источник питания с согласованным напряжением от 14 до 48 В постоянного тока. Подключение с последовательной нагрузкой осуществляется между контактом 20 (+) и контактом 19 (–).
Основные характеристики модуля
- Измерение напряжения RMS (0…300 В) или тока (0…5 А).
- Предназначен для стандартной работы с частотами от 45 до 1000 Гц (расширенный диапазон до 20 кГц).
- Совместим со стандартными трансформаторами тока и потенциальными трансформаторами.
- Отраслевые стандарты выхода: 0...1, 0...20, 4...20 мА, 0...5 или 0...10 В постоянного тока.
- Точность ±0,25%, калибруется на производстве.
- Гальваническая изоляция на основе трансформатора 1500 В (среднеквадратическое значение).
- Защита от перегрузки по входу до 480 В макс. (пиковый и постоянный ток) или 10 А RMS непрерывно.
- Сертификаты ANSI/IEEE C37.90.1-1989, CSA, FM.
Модуль DSCA33
Модуль ввода DSCA33 True RMS (рис. 6) по всем основным характеристикам идентичен SCM5B33. Отличие состоит в его конструктиве, оптимизированном для размещения на DIN-рейке.
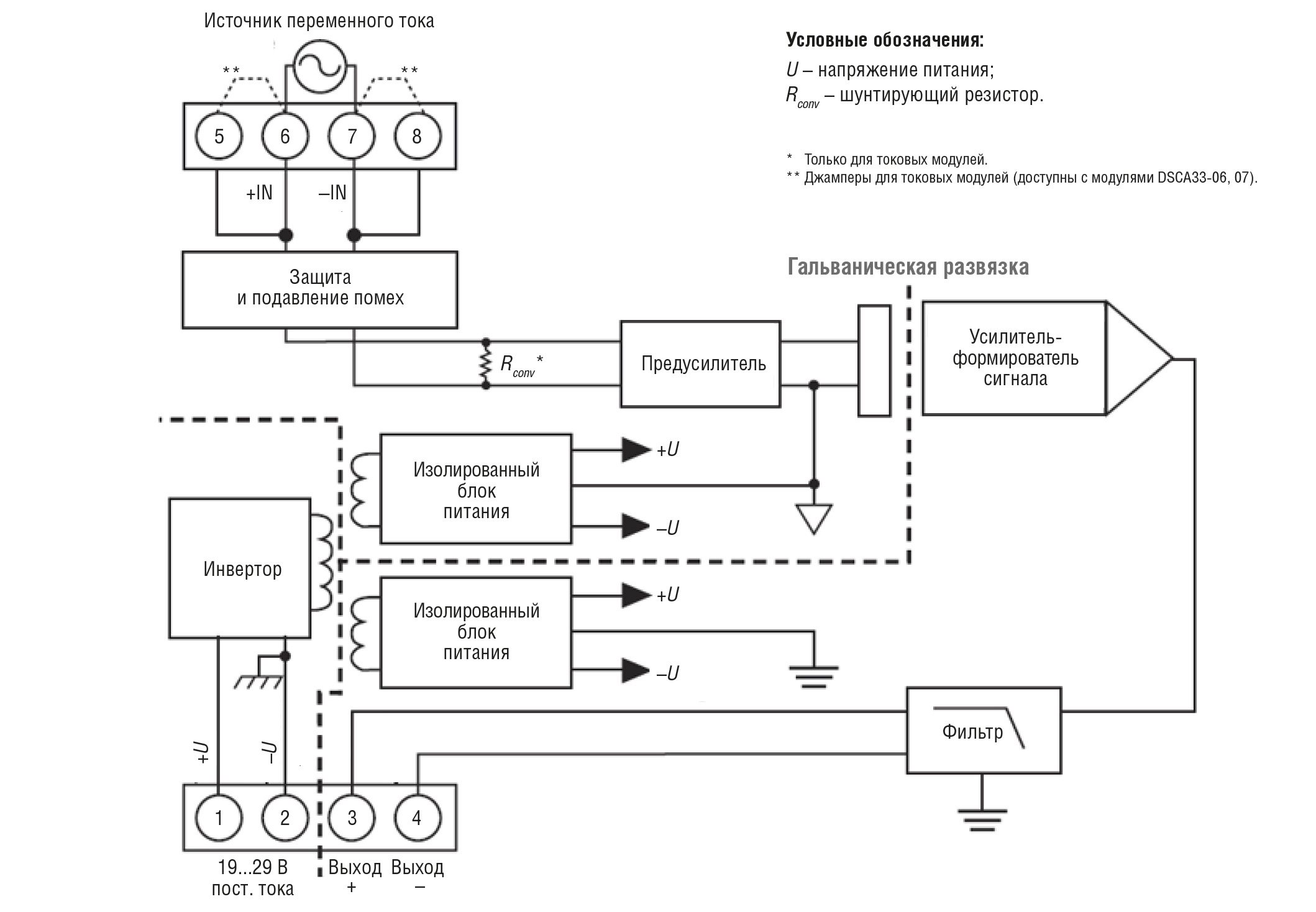
Модули DSCA33 обладают превосходной стабильностью во времени и не требуют повторной калибровки, однако в ситуациях, когда необходима точная настройка, это можно сделать вручную. Регулировки выполняются с помощью потенциометров, расположенных под этикеткой на передней панели, и не являются интерактивными.
Заключение
Итак, мы увидели, что измерить и рассчитать действующее значение тока или напряжения в условиях нестабильных показателей сетей реального производства не так-то просто: для этого требуется привлечение довольно сложного математического аппарата либо использование готовых качественных измерительных модулей из разряда рассмотренных в этой статье. Второе, разумеется, будет более практичным и простым решением. Что же касается надёжности и качества этих модулей Dataforth, то можно отметить их широкий диапазон рабочих температур –40…+80°C, малую погрешность измерений (класс точности 0,2), как для синусоидальных, так и для несинусоидальных токов, а также соответствие требованиям директивы 2014/34/EU (ATEX) для взрывозащищённого оборудования. ●
Статья подготовлена по материалам компании Dataforth
E-mail: textoed@gmail.com
Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!