Многократные измерения
В системах промышленной автоматизации в некоторых случаях измерения выполняют многократно, а полученные результаты усредняют с целью повышения точности. При этом возникает вопрос, существует ли граница повышения точности. Сколько измерений нужно делать на практике? Интуитивно ясно, что усреднение приводит к уменьшению погрешности, поскольку результаты отдельных измерений имеют как положительные, так и отрицательные отклонения от точного значения и поэтому частично взаимно компенсируются. С ростом числа измерений среднее значение отрицательных отклонений приближается по модулю к среднему значению положительных и точность их взаимной компенсации улучшается. Для практики важно получить количественную зависимость между числом измерений и погрешностью усреднённого результата. Вопросам повышения точности путём многократных измерений посвящён ГОСТ 8.207-76 [1], однако он не даёт ответа на поставленные вопросы.
Понятия корреляции, точности, разрешающей способности и порога чувствительности
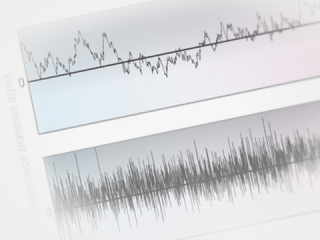
Погрешности измерений могут быть коррелированными и некоррелированными случайными величинами. Поскольку многократные измерения выполняются последовательно во времени, то серию измерений можно представить как выборки из реализации некоторого случайного процесса x(t). Если функция x(t) имеет ограниченный по частоте спектр, то при растяжении графика во времени наступает момент, когда он начинает выглядеть не как шум, а как извилистая кривая (рис. 1 а).
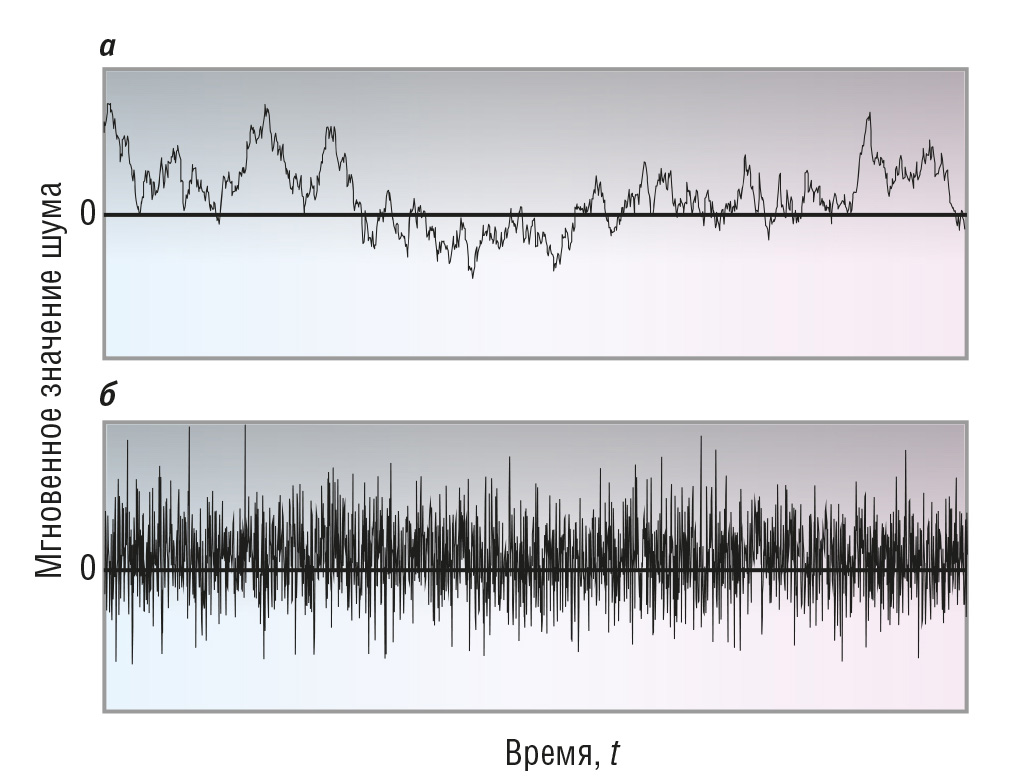
При достаточно малом сдвиге по времени τ функции относительно самой себя значения функции на рис. 1 а будут различаться слабо (при нулевом сдвиге не будут отличаться вообще), а на рис. 1 б – сильно даже при как угодно малом τ. Количественно эти свойства случайных функций описываются функцией автокорреляции:
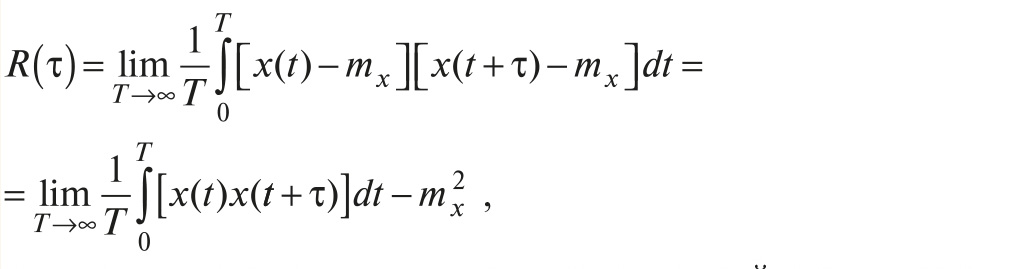
где mx – математическое ожидание случайного процесса, T→∞ – интервал наблюдения.
В нашем примере на рис. 1 а случайный процесс называют коррелированным, а на рис. 1 б – некоррелированным (белым шумом).
Часто используется понятие интервал корреляции, или время корреляции, под которым понимается величина временного сдвига τк, при превышении которого корреляцией можно пренебречь в условиях конкретного эксперимента. Обычно интервал корреляции определяют как
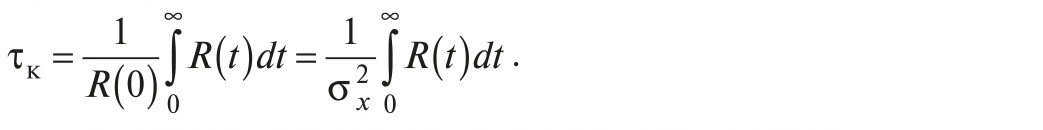
Если интервал корреляции равен нулю, то случайный процесс называют некоррелированным, или белым шумом. В противном случае он считается коррелированным. Все реальные процессы являются коррелированными, поскольку имеют ограниченную мощность и, следовательно, ограниченную полосу частот. Однако на определённом интервале времени (частот) их можно приближённо считать некоррелированными.
Рассмотрим теперь понятия точности, разрешающей способности и порога чувствительности. Точность (погрешность) характеризует степень отличия результата измерения от точного значения, связанного с эталоном единицы физической величины. Разрешающая способность показывает, какое минимальное отклонение измеряемой величины может быть зарегистрировано измерительным прибором. Порог чувствительности – это наименьшее значение физической величины, начиная с которого может осуществляться её измерение данным средством. Например, если модуль ввода в диапазоне измерений –10...+10 В имеет погрешность ±0,05%, то его порог чувствительности равен ±5 мВ. Однако благодаря наличию 16-разрядного АЦП этот модуль может различить два входных сигнала, отличающихся на 20/216 = 0,3 мВ, то есть его разрешающая способность в ±5/0,3 = ±16 раз выше порога чувствительности. Отметим, что это справедливо при условии, что уровень собственных шумов модуля ввода ниже величины младшего значащего разряда (МЗР), то есть погрешность является чисто систематической.
Порог чувствительности, который определяется погрешностью измерений, может быть гораздо больше, чем разрешающая способность, поскольку при определении погрешности учитывают:
-
нелинейность измерительного прибора во всём диапазоне измерений;
-
динамику процесса старения прибора;
-
технологический разброс метрологических параметров от прибора к прибору;
-
не только систематическую, но и случайную некоррелированную компоненту погрешности, которая может быть уменьшена до уровня МЗР путём многократных измерений с последующим усреднением результатов.
Разрешающая способность не зависит от перечисленных факторов, и это объясняет её отличие от порога чувствительности и погрешности. Разрешающая способность увеличивается при уменьшении случайной составляющей погрешности.
Приведём несколько примеров, когда требования к погрешности на несколько порядков могут отличаться от требований к разрешающей способности.
Пример 1
Предположим, имеется релейный регулятор, который в соответствии с алгоритмом своей работы должен определить знак разности между температурой в печи и значением уставки. Если для измерения температуры используется термопара с датчиком температуры холодного спая с погрешностью измерений 2°C, то для измерения температуры в диапазоне 0...100°C достаточно 50 уровней квантования, что может быть обеспечено 6-разрядным АЦП. Если же использовать 16-разрядный АЦП, то разрешающая способность по температуре составит 100/216 = 0,0015°C. В случае применения 6-разрядного АЦП колебания температуры в процессе регулирования не могут быть менее 2°С, в то время как при использовании 16-разрядного АЦП амплитуда колебаний приближается к 0,0015°C. Такой регулятор используется, когда важна стабильность во времени, а не точность соответствия уставке. Например, стабильность (а не точность) важна для термостатов, которые используются при калибровке термодатчиков методом сличения с показаниями образцового прибора. Напомним, что альтернативным вариантом является калибровка с помощью калибратора (задатчика), который должен иметь высокую точность (и одновременно стабильность) задания температуры.
Пример 2
В элеваторах для хранения растительного сырья наблюдается эффект самосогревания, связанный в основном с деятельностью микроорганизмов. Для обеспечения надлежащего качества зерна абсолютное значение температуры достаточно знать с погрешностью в несколько градусов, но факт её роста желательно фиксировать с разрешающей способностью 0,1...0,01°С. Высокая разрешающая способность позволяет предупредить развитие очага самосогревания на ранней стадии и расположить датчики температуры на большом расстоянии один от другого.
Пример 3
Если требуется обнаружить момент времени начала химической реакции по признаку начала роста температуры, то необходим прибор с высокой разрешающей способностью, но не обязательно с высокой точностью.
Пример 4
Пусть требуется оценить параметры колебательного процесса: декремент затухания колебаний, период колебаний, коэффициент нелинейных искажений, длительность переходного процесса, величину помехи на фоне полезного сигнала. Для оценки всех перечисленных параметров находится соотношение ординат или абсцисс функции в разных её точках, то есть пропорции между отдельными частями графика, которые не зависят от самого значения функции. Поэтому такие измерения могут быть выполнены прибором, имеющим низкую точность, но высокую разрешающую способность. Дополнительным требованием в этом примере является достаточная линейность измерительного канала в рассматриваемом диапазоне.
Для улучшения разрешающей способности при низкой точности используется «электронная лупа» (аналогичная опция в фотоаппаратах называется zoom). В основе принципа работы «электронной лупы» лежит свойство любых нелинейностей f(x) приближаться к линейным зависимостям
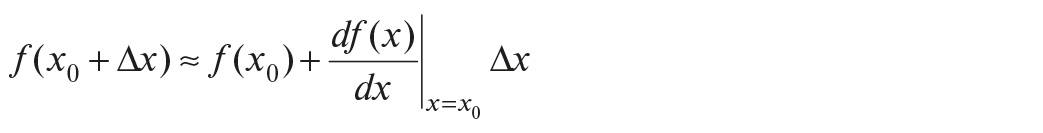
при малых Δx, что обеспечивает отсутствие нелинейных искажений формы исследуемого сигнала. Работа «электронной лупы» состоит в том, что из исследуемого сигнала вычитается некоторый постоянный уровень f(x0), а разность усиливается с помощью аналогового усилителя или квантуется АЦП с высокой разрядностью. При этом величина постоянного уровня может быть задана с низкой точностью, поскольку целью является измерение соотношений отдельных участков сигнала между собой, а не относительно единицы физической величины.
Отметим, что понятие разрешающая способность отсутствует в руководстве по метрологии РМГ 29-99 [2]. Причина, вероятно, в том, что данное понятие не связано с измерением как операцией сличения с эталоном, но связано с оценкой отношений между физическими величинами, ни одна из которых не является эталоном, а это согласно РМГ 29-99 не относится к измерениям.
Точность, разрешающая способность и порог чувствительности в общем случае выше у АЦП с большим числом двоичных разрядов, хотя прямой связи здесь нет. АЦП с высокой разрядностью может иметь большой уровень шумов, высокую нестабильность источника опорного напряжения и связанную с этими особенностями низкую точность.
Усреднение результатов некоррелированных измерений
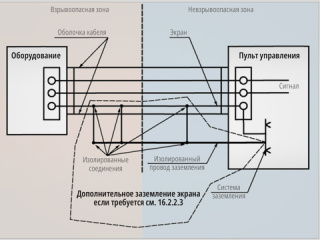
Рассмотрим некоторое средство измерений, например измерительный модуль аналогового ввода NL-8AI (НИЛ АП) для измерения и ввода в компьютер значений напряжения x (рис. 2).
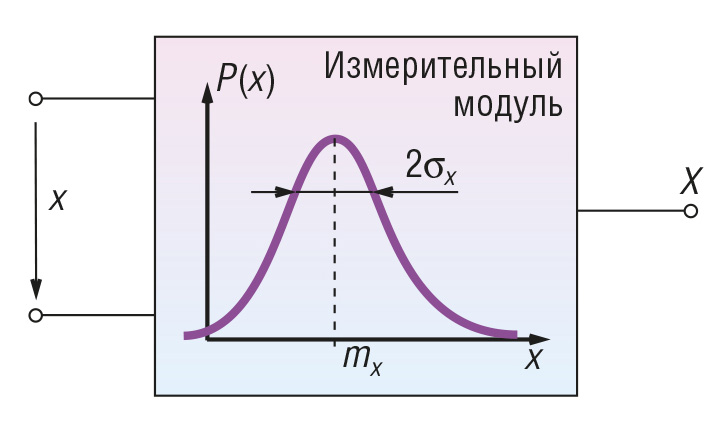
В общем случае на датчик, линию связи между датчиком и модулем и сам модуль действуют электромагнитные помехи и собственные шумы операционных усилителей, АЦП, резисторов, микропроцессорной части модуля и т.п. [3]. Мы не будем рассматривать помехи, действующие на объект измерений, поскольку он не входит в состав измерительного канала.
Указанные причины приводят к тому, что результат измерения становится случайной величиной, значение которой изменяется от измерения к измерению. Случайная величина X может быть описана некоторой функцией распределения c математическим ожиданием M(X) = mx и среднеквадратическим отклонением σx, которое принимается за случайную составляющую погрешности измерительного прибора. Дисперсия случайной величины D(X) = σx2.
Погрешность средства измерений определяется изготовителем и указывается в эксплуатационной документации.
В величину погрешности входит как систематическая, так и случайная составляющая. Если случайная составляющая превышает 10% от систематической, то она указывается отдельно (ГОСТ 8.009-84 [4]). Иногда случайная составляющая указывается с помощью автокорреляционной функции или спектральной плотности мощности.
Случайная составляющая погрешности может быть снижена путём усреднения результатов многократных измерений. Если в составе погрешности преобладает систематическая компонента, то усреднение не приводит к повышению точности. О наличии случайной составляющей можно судить по рассеянию результатов однократных измерений.
Предположим, что с помощью измерительного модуля выполнено N измерений, в результате которых получены значения x1, x2,…xN. Усреднение результатов измерений выполняется по формуле среднего арифметического значения:

Однако xср также является случайной величиной, поскольку, выполняя несколько серий измерений и усредняя каждую из них, мы получим отличающиеся друг от друга средние значения xср для каждой серии. Но xср будут иметь меньшую дисперсию (среднеквадратическое отклонение), чем измерительный прибор. Покажем это.
Будем считать, что результаты измерений x1, x2,…xN являются независимыми случайными величинами (выборками из некоррелированного случайного процесса). Тогда дисперсия их среднего арифметического будет равна
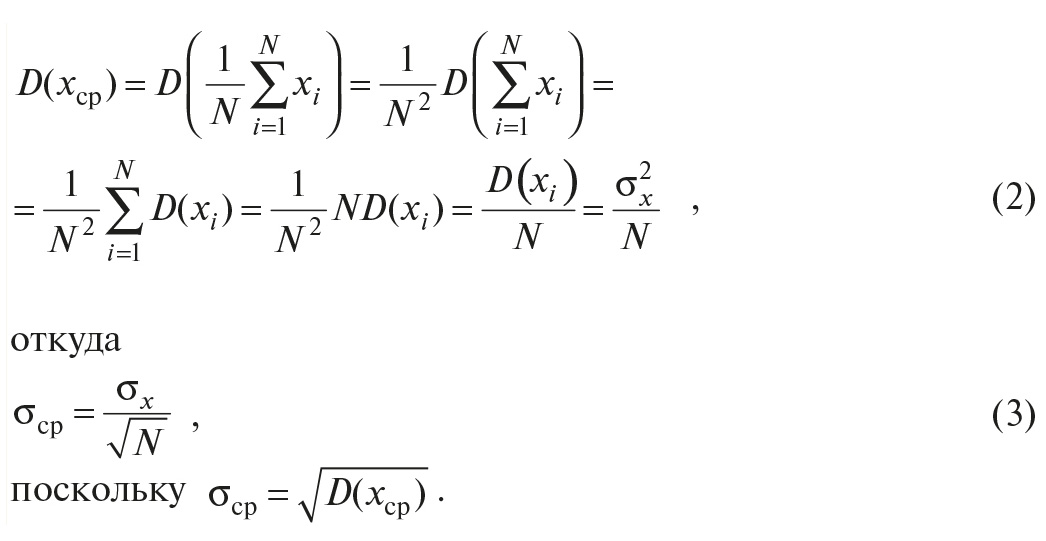
В (2) использованы два свойства оператора дисперсии:
а) дисперсия произведения случайной величины и константы равна дисперсии случайной величины, умноженной на квадрат константы, и б) дисперсия суммы случайных величин равна сумме дисперсий каждой из них [5]. Кроме того, считается, что все измерения выполнены одним и тем же прибором, то есть дисперсии всех измерений одинаковы и равны D(xi) = δx2, а случайные величины являются некоррелированными.
Докажем первое из использованных свойств (подробнее см. [5]). По определению дисперсии D(X) и математического ожидания M(X) = mx случайной величины X имеем

Докажем теперь, что дисперсия суммы случайных величин равна сумме их дисперсий. Для этого сначала докажем, что математическое ожидание суммы случайных величин равно сумме их математических ожиданий, то есть

Сумма случайных величин X+Y – это такая случайная величина, которая принимает все возможные комбинации сумм случайных величин X и Y, то есть X+Y = {x1+y1, x1+y2, x2+y1, x2+y2,…, xN+yN}. Поэтому по определению математического ожидания получим:
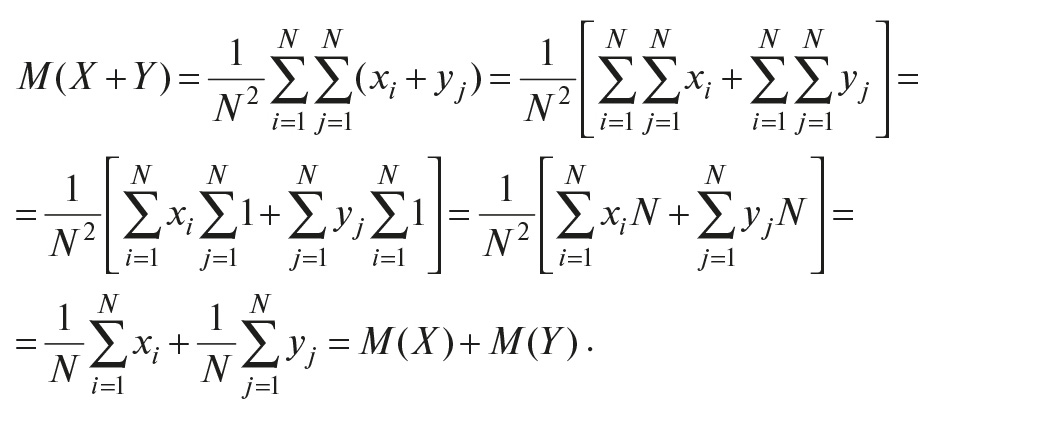
Аналогичное соотношение для N случайных величин можно доказать путём попарной группировки случайных величин. Формула (5) доказана.
Выведем ещё вспомогательное равенство, связывающее дисперсию случайной величины с математическим ожиданием. Пользуясь определением дисперсии (4), получим:
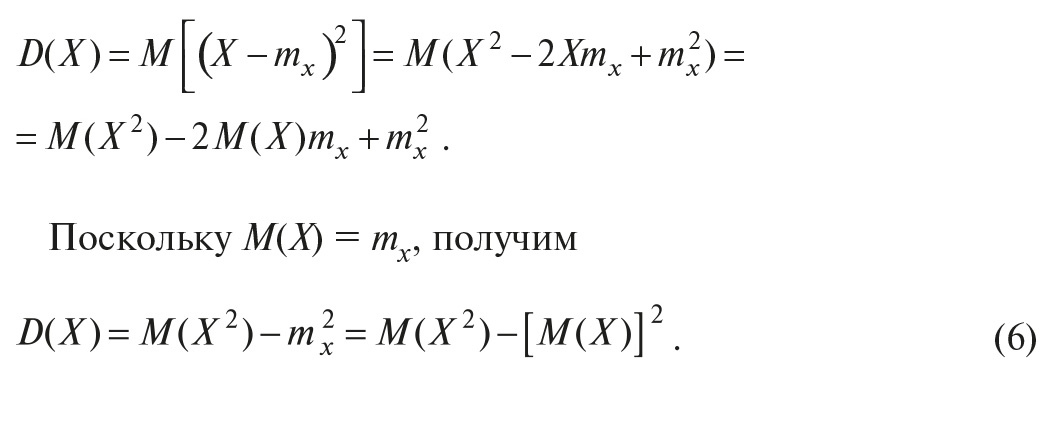
Пользуясь соотношениями (5) и (6), получим дисперсию суммы двух случайных величин в виде:
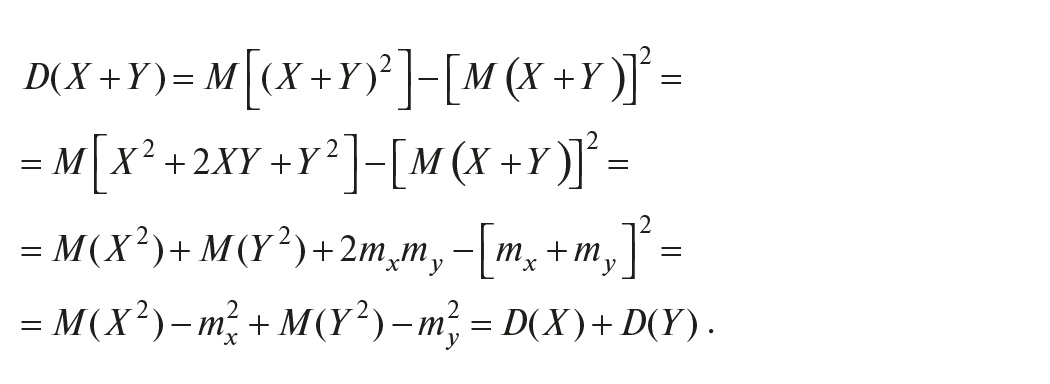
Однако это утверждение справедливо при соблюдении нескольких условий, выполнимость которых довольно трудно проверить на практике.
Во-первых, усреднение даёт эффект только для случайной составляющей погрешности. Погрешность измерений перестаёт уменьшаться, когда σср становится настолько малой, что суммарная погрешность определяется систематической составляющей. Систематическая погрешность складывается из нелинейности АЦП и операционных усилителей, температурной зависимости напряжения смещения нуля и коэффициента передачи измерительного канала (температурно-зависимые погрешности учитываются как дополнительные), низкочастотных шумов, у которых время автокорреляции больше времени выполнения серии повторных измерений (к ним относится, в частности, «старение» элементов), динамической погрешности. Практически редко удаётся снизить общую погрешность измерений более чем в 2-3 раза с помощью усреднения.
Во-вторых, результаты измерений должны быть статистически независимы, то есть интервал времени между соседними измерениями должен быть много больше времени автокорреляции случайной погрешности. Посмотрим на рис. 3: если при белом шуме средние значения за интервалы времени Δt1 и Δt2 равны между собой (рис. 3 б), то при коррелированном шуме – не равны (рис. 3 а). Например, усреднение даже 100 измерений в течение 10 с не может скомпенсировать компоненты шума, спектр которых лежит ниже 0,1 Гц.
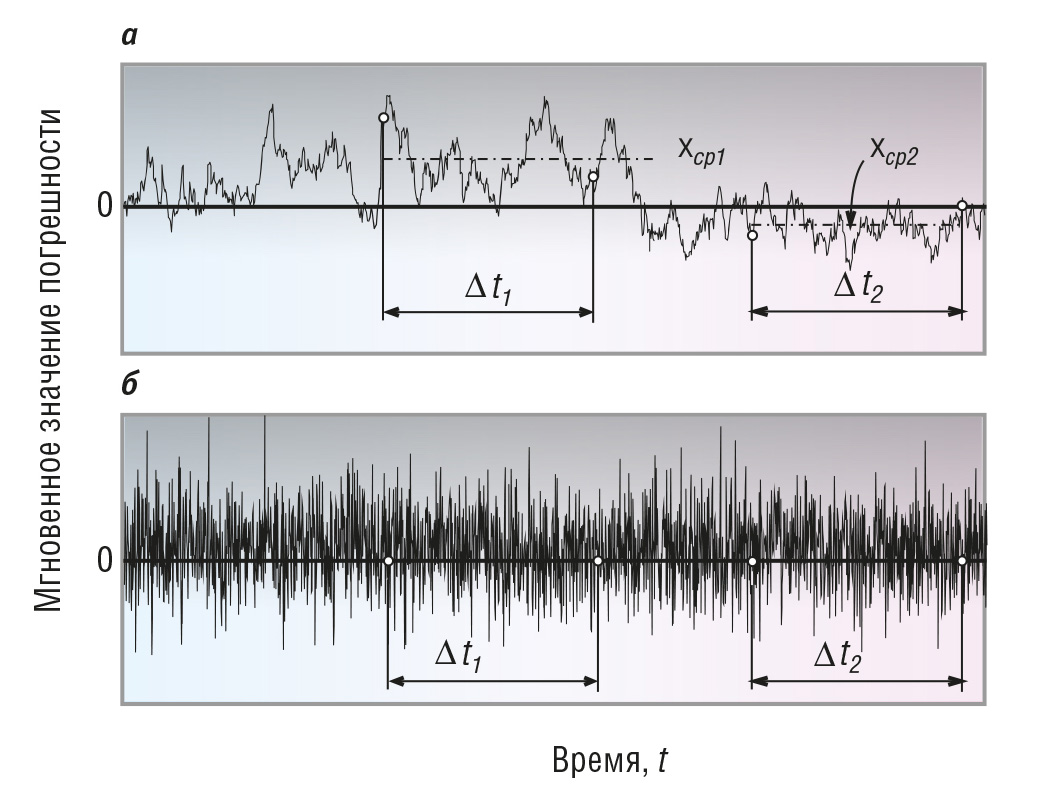
Требование статистической независимости измерений не выполняется, в частности, и в случае, когда действует искусственная помеха, делающая шум цветным (коррелированным), например помеха от сотового передатчика на крыше здания, от радиотелефона, из сети 50 Гц, от сварочного аппарата, от молнии, от внутренних генераторов измерительного прибора, от электродрели и т.п. В этих случаях усреднение также ослабляет помеху, но уже не в √Nраз (подробнее об этом будет рассказано далее).
Особо следует отметить, что как систематическая, так и случайная составляющая погрешности средств измерений являются случайными величинами. Однако между ними имеется принципиальное различие. Систематическая погрешность является случайной на множестве средств измерений, но детерминированной для каждого образца из множества. Поэтому систематическую погрешность невозможно уменьшить путём многократных измерений одним и тем же прибором, но можно уменьшить, усредняя результаты, полученные измерением с помощью множества средств измерений одного типа. Случайная же погрешность является случайной на множестве результатов измерений одним и тем средством измерений, и поэтому её можно уменьшить путём усреднения результатов многократных измерений.
В отличие от погрешности разрешающая способность не зависит от величины систематической погрешности и поэтому может быть увеличена существенно. Она может стать даже меньше величины младшего значащего разряда АЦП при условии, если стабильность его уровней позволяет это сделать.
Если в паспорте на средство измерения не указана величина случайной составляющей погрешности, её можно оценить по результатам измерений:

где коэффициент M зависит от количества измерений N. При N>60 он равен единице, при N<60 о выборе этого коэффициента см. в [6].
Мы рассмотрели случай, когда отдельные измерения не коррелированы. В случае коррелированных измерений можно показать, что среднеквадратическое отклонение усреднённого результата N измерений будет описываться выражением:
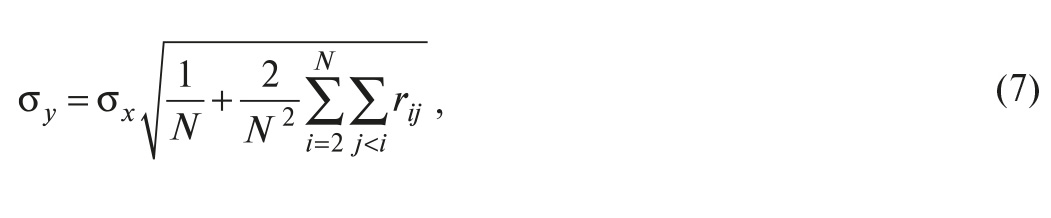
где rij – элементы корреляционной матрицы N измерений. ●
Литература
-
ГОСТ 8.207-76. Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения.
-
РМГ 29-99 ГСИ. Метрология. Основные термины и определения.
-
Денисенко В.В. Компьютерное управление технологическим процессом, экспериментом, оборудованием. – М. : Горячая линия-Телеком, 2009. – 608 с.
-
ГОСТ 8.009-84. Государственная система обеспечения единства измерений. Нормируемые метрологические характеристики средств измерений.
-
Гмурман В.Е. Теория вероятностей и математическая статистика. – М. : Высшая школа, 2001. – 479 с.
-
Орнатский П.П. Теоретические основы информационно-измерительной техники / 2-е изд. – Киев : Вища школа, 1983. – 455 с.
Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!