Термопреобразователи сопротивления

Термопреобразователи сопротивления [1] (терморезисторы, резистивные термопреобразователи, термометры сопротивления) являются вторыми по распространённости средствами измерения температуры после термопар. Принцип их действия основан на зависимости электрического сопротивления металла (по ГОСТ 6651-2009 [2] используется медь, платина и никель) или полупроводника от температуры.

Достоинством металлических датчиков является высокая линейность и взаимозаменяемость, то есть возможность замены вышедшего из строя датчика на аналогичный без повторной юстировки системы. Взаимозаменяемость достигается благодаря малому технологическому разбросу сопротивлений датчиков (разброс температуры составляет от ±0,15°С при температуре 0°С для медных датчиков класса допуска А до ±0,6°С для датчиков класса С по ГОСТ 6651-2009). Разброс сопротивлений увеличивается с ростом температуры. Медные датчики используются для измерения температуры в диапазоне от –180 до +200°С, платиновые – в диапазоне от –200 до +850°С, никелевые – от –60 до +180°С [2].

Никелевые термопреобразователи имеют высокую чувствительность, платиновые – высокую стабильность (неизменность показаний с течением времени), медные – низкую цену и наилучшую линейность зависимости сопротивления от температуры.

Нормируемыми параметрами металлических термопреобразователей являются сопротивление R₁₀₀ при 100°С и температурный коэффициент термопреобразователя сопротивления α=(R₁₀₀ – R₀₎ / R₀•100ºC, где – сопротивление при 0°С. Медные датчики из­го­тавливаются с α=0,00428ºC^–1, плати­но­вые – c α=0,00385ºC^–1 и α=0,00391ºC^–1, никелевые – с α=0,00617ºC^–1. В маркировке, приводимой на корпусе датчика или прикреплённой к нему бирке, по ГОСТ 6651-2009 должны указываться следующие данные: модификация датчика по номенклатуре изготовителя, число чувствительных элементов (если их более одного), класс допуска, схема соединения выводов, диапазон рабочих температур.

Зависимость сопротивления от температуры R (t) в узком диапазоне температур приближённо можно считать линейной (рис. 1).

 

 

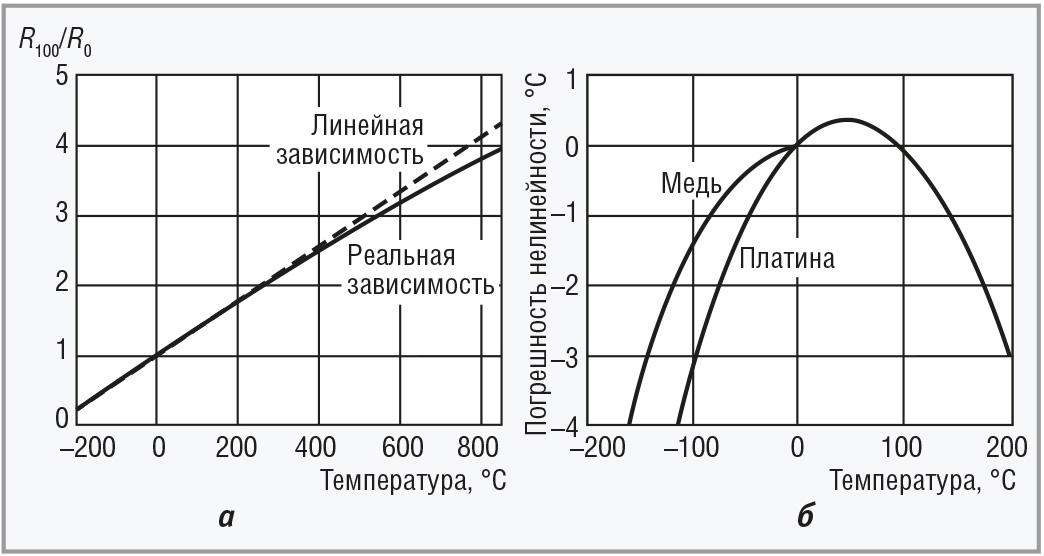
В широком диапазоне температур линейная зависимость даёт слишком большую погрешность (рис. 1б), поэтому ГОСТ 6651 [2] устанавливает для термопреобразователей сопротивления табличную или полиномиальную аппроксимацию экспериментально полученной зависимости сопротивления от температуры [2]. Это позволяет исключить систематическую составляющую погрешности нелинейности из результата измерений. Процедура исключения погрешности нелинейности обычно выполняется в микроконтроллере модуля ввода [1].

После исключения систематической составляющей погрешности нелинейности остаётся случайная составляющая, обусловленная технологическим разбросом сопротивления датчика при 0°С и разбросом его температурного коэффициента сопротивления. Эта погрешность вносит основной вклад в результат измерения температуры. Она нормируется для четырёх классов допуска: АА, А, B и С [2].

Источником погрешности измерений с помощью термопреобразователей сопротивления является также электро-термический эффект, который проявляется при соединении никелевых или медных термопреобразователей с медными проводами. Обычно он не превышает 20 мкВ. Для уменьшения этого эффекта используют среднее значение двух измерений при противоположных направлениях тока или измерения на переменном токе [3].

Датчик температуры, основанный на зависимости сопротивления от температуры, состоит из термочувствительного элемента и защитной оболочки. Чувствительный элемент (сенсор) может быть изготовлен в виде катушки с бифилярной намоткой (безиндуктивная намотка сдвоенным проводом) или в виде проводникового слоя металла, нанесённого на диэлектрическое основание.

При использовании крупных датчиков для измерения температуры тел с малой теплоёмкостью появляется методическая погрешность, вызванная перераспределением количества теплоты между объектом измерений и датчиком (погрешность термического шунтирования). Для уменьшения этой погрешности следует правильно выбирать размер (теплоёмкость) датчика или учитывать эту погрешность расчётным путём.

Для датчиков с малыми геометрическим размерами существенную роль играет величина измерительного тока I_ex (здесь индекс ex происходит от “excitation” – «возбуждение»). Мощность I_ex²R(t), выделяемая при прохождении измерительного тока через датчик с сопротивлением R(t), преобразуется в тепло, вызывающее саморазогрев датчика. Для уменьшения эффекта саморазогрева следует снижать величину измерительного тока, однако это приводит к уменьшению отношения сигнала к шуму и увеличению случайной составляющей погрешности измерений. Лучшие результаты даёт измерение с помощью импульса, длительность которого выбирается из условия минимизации энергии, поступающей в резистор за время измерения.

В отличие от металлических термопреобразователей полупроводниковые терморезисторы, как правило, требуют индивидуальной градуировки и не обеспечивают взаимозаменяемости. Их достоинствами являются малые размеры, низкая стоимость и высокая чувствительность к изменению температуры.

Для измерения температуры с помощью термопреобразователей сопротивления необходимо измерять величину омического сопротивления датчика. В системах промышленной автоматизации используются три варианта схем измерений: двухпроводная, трёхпроводная и четырёхпроводная.

Двухпроводная схема измерений

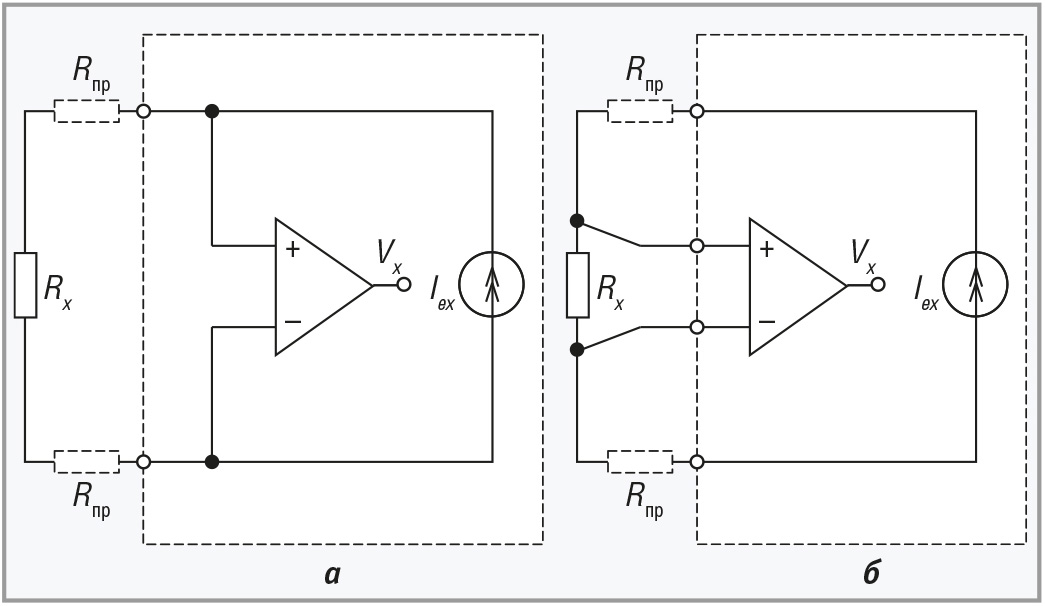
Двухпроводная схема измерений (рис. 2) использует косвенный метод измерений, при котором измеряется напряжение на сопротивлении V_x, вызванное протекающим калиброванным током возбуждения I_ex. 

Реже задаётся калиброванное напряжение V_x и измеряется ток I_ex. Возможен также вариант, когда одновременно измеряются как ток, так и напряжение при использовании некалиброванных источников измерительных сигналов. Во всех случаях величину сопротивления R_x рассчитывают по формуле 

В связи с тем, что сопротивление металлических датчиков мало, большую погрешность в результат измерения вносят сопротивления проводов R_пр (рис. 2а). Поэтому двухпроводная схема измерений используется, когда сопротивления R_пр малы, например, не превышают 0,1% от сопротивления датчика R₀, то есть для медного датчика ТСМ50 с R₀ = 50 Ом сопротивление проводов должно быть не более 0,05 Ом. При использовании проводов сечением 0,35 мм² с погонным сопротивлением 0,049 Ом/м длина пары проводников для этого случая не должна превышать 0,5 м.

Поскольку рассматриваемая погрешность является систематической, её можно исключить из результата измерений несколькими способами. Если измерения выполняются при заранее известном сопротивлении проводов R_пр, то величину измеренного сопротивления нужно уменьшить на R_пр. Для более точного исключения этой погрешности нужно учесть зависимость сопротивления от температуры, если известна температура провода.

Относительную погрешность измерения сопротивления по двухпроводной схеме можно получить из выражения (2), с учётом погрешности, вызванной нескомпенсированной составляющей сопротивления проводов ΔR_пр: 

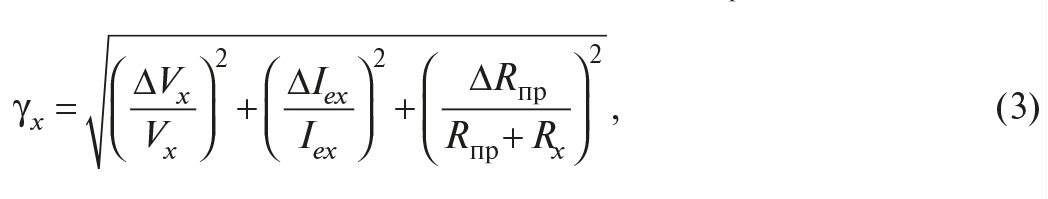
где ΔV_x – погрешность измерения напряжения; ΔI_ex – погрешность задания тока. Здесь использовано квадратичное суммирование погрешностей, поскольку все они являются случайными. В случае, когда сопротивление проводов не вычитается из результата измерения, ΔR_пр = 2R_пр, и эта погре­­­­шность должна учитываться алгебраически.

Четырёхпроводная схема измерений

Принцип действия четырёхпроводной схемы (рис. 2б) основан на измерении напряжения не на выводах источника тока, как на рис. 2а, а непосредственно на выводах сопротивления R_x. При этом падение напряжения на сопротивлении проводов R_пр не влияет на результат измерения.

Методическая погрешность в рассматриваемой схеме отсутствует, и относительная погрешность измерения сопротивления определяется только инструментальной погрешностью измерения напряжения и задания тока: 

Расстояние от модуля ввода до датчика при четырёхпро­-водной схеме измерений ограничивается только уровнем помех, который растёт пропорционально длине проводов.

Трёхпроводная схема измерений

Желание снизить стоимость кабеля в системах автоматизации при невысоких требованиях к точности привело к появлению трёхпроводной схемы измерений. В модулях ввода используются три варианта трёхпроводных схем измерения сопротивлений, которые отличаются погрешностью и конструкцией измерительного модуля.

С появлением интегральных АЦП с двумя встроенными цифроуправляемыми источниками тока возникла возможность реализовать трёхпроводную схему измерений, показанную на рис. 3а.

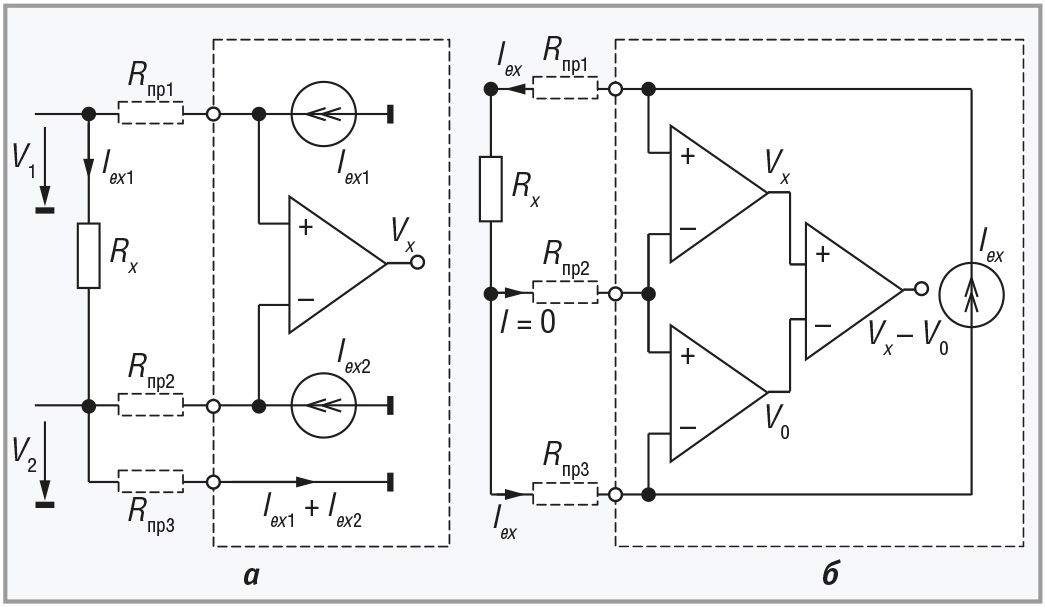
Предположим сначала, что равны токи источников тока I_ex1 = I_{ex2 =} I_ex и сопротивления проводов: R_пр1 = R_пр2 = R_пр, а погрешность измерителя напряжения равна нулю. Тогда напряжение V_x между выводами измерителя напряжения на рис. 3а будет равно 

 

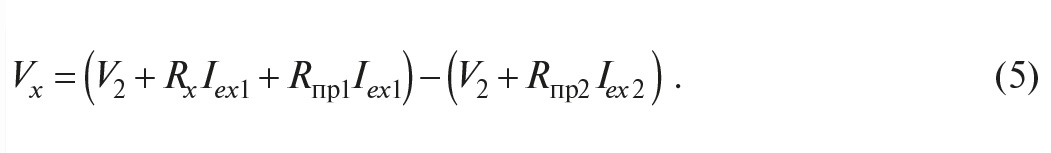
Учитывая идентичность токов и сопротивлений, получим

 

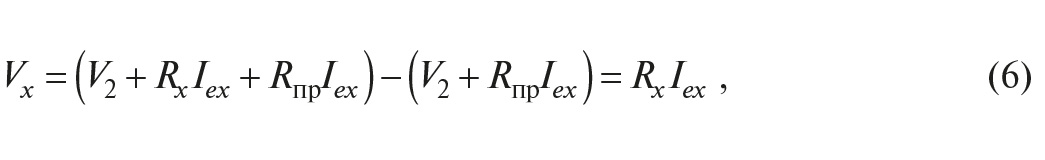
то есть падения напряжения на проводах взаимно компенсируются благодаря идентичности измерительных токов и сопротивлений проводов.

Предположим теперь, что токи I_ex1 и I_ex2 заданы со случайной погрешностью ΔI_ex , то есть I_ex1 = I_ex ± ΔI_ex, I_ex2 = I_ex ± ΔI_ex и сопротивления проводов также имеют технологический разброс R_пр1 = R_пр ± ΔR_пр, R_пр2 = R_пр ± ΔR_пр , а погрешность измерителя напряжения равна Δ_V. Тогда выражение (5) примет вид 

 

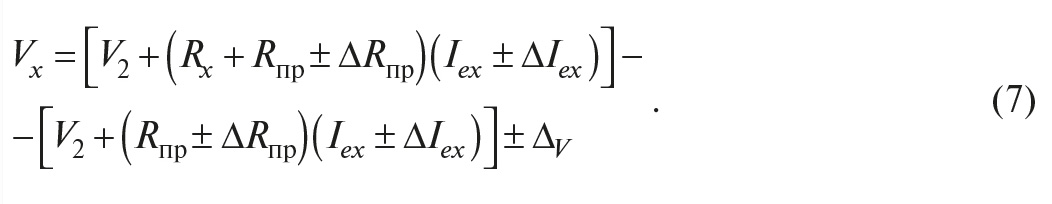
Пренебрегая выражениями вида ΔR_прΔI_ex по сравнению с R_прI_ex и с ΔR_прI_ex, получим:

 

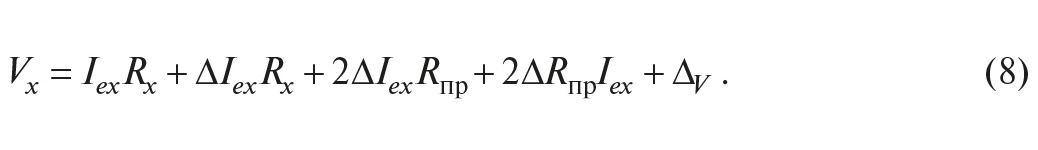
Используя правило квадратичного суммирования случайных погрешностей, получим выражение для среднеквадратической погрешности измерения напряжения:

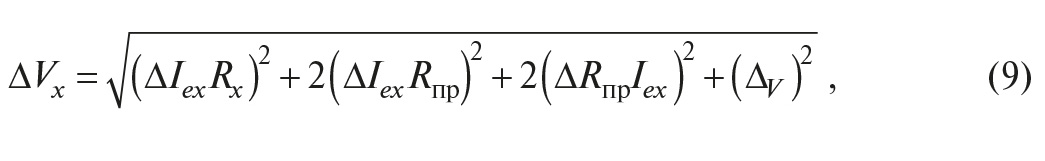
то есть

Относительную погрешность измерений с помощью трёхпроводной схемы, показанной на рис. 3а, можно рассчитать по формуле (4), используя (9).

Как следует из (9) и (4), погрешность пропорциональна сопротивлению (длине) провода R_пр и дисбалансу токов источников измерительного тока. Заметим, что обе эти составляющие отсутствуют в ранее рассмотренной четырёхпроводной схеме измерений.

Второй вариант трёхпроводной схемы измерений показан на рис. 3б. Компенсация падений напряжения на проводах в ней осуществляется благодаря применению второго измерителя напряжения V₀. Зная величину V₀ и предполагая, что сопротивления R_пр1 = R_пр3 (сопротивление R₂ не вносит погрешность, так как ток через него равен нулю), получим:

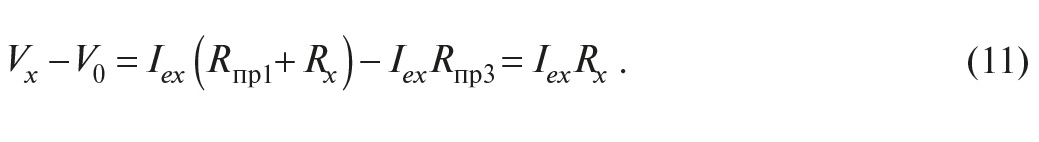
В этой схеме присутствуют те же источники погрешности, что и в предыдущей, поскольку используется тот же принцип компенсации погрешностей, если учесть, что вместо погрешности задания тока вносится погрешность его измерения.

Третьим вариантом трёхпроводной схемы измерения сопротивлений является мост Уитстона (рис. 4). 

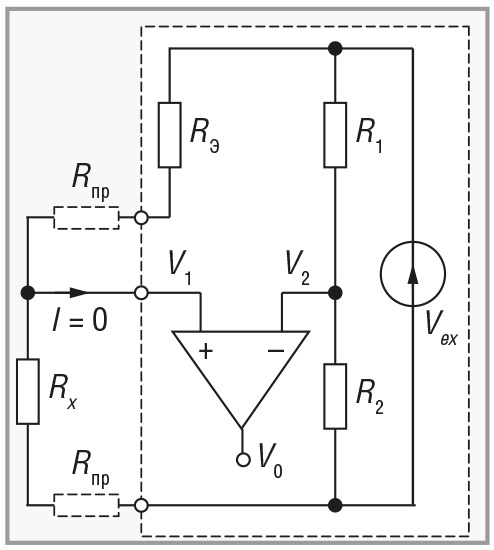
В отличие от предыдущих схем, в которых использован косвенный метод измерения сопротивлений, мост используется для прямого измерения методом сличения с эталоном. В процессе измерений мост служит индикатором равенства напряжений левого V₁ и правого V₂ плеча моста:

 

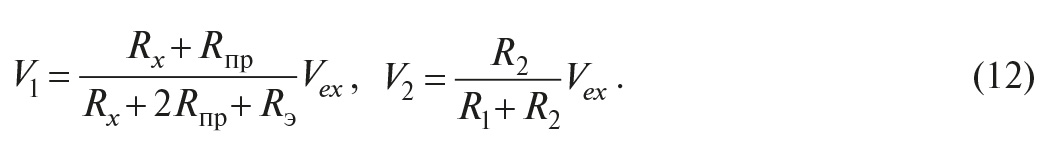
До появления микропроцессорных измерительных средств процесс измерения сопротивлений с помощью моста выполнялся следующим образом. В качестве R_э использовался магазин эталонных сопротивлений, которые переключались вручную или специальным механическим приводом до тех пор, пока не наступало состояние равно­весия моста, когда V₀ = 0, или V₁ = V₂ . В состоянии равновесия, как следует из (12),

 

Зная R₁, R₂, R_э, и R_пр, из (13) можно найти искомое значение R_x. Важно, что результат измерения не зависит от напряжения V_ex, в том числе его стабильности и величины помех в цепях питания моста.

Если мост уравновешен при условии R₁/R₂=1, то, как следует из (13), R_x = R_э, при этом сопротивление проводов R_пр не влияет на результат измерения.

В модулях аналогового ввода описанный метод измерения в принципе возможен с помощью цифроуправляемого эталонного резистора [4, 5], однако экономически эффективнее использовать рассмотренные в статье схемы с источниками тока.

Современные модули ввода сигналов термопреобразователей сопротивления используют все три схемы измерения сопротивлений: двухпроводную, трёхпроводную и четырёхпроводную. Например, модуль NL-4RTD НИЛ АП имеет 6 источников тока I_ex0 +...I_ex2 +, I_ex0 –...I_ex2 – и 4 дифференциальных потенциальных входа (Sence0+,Sence0−…Sence3+,Sence3−). Это позволяет подключить к нему 4 датчика по двухпроводной схеме или 4 датчика по четырёхпроводной схеме, или 3 датчика по трёхпроводной схеме измерений, показанной на рис. 3а.

Погрешность измерений

Погрешность измерений температуры с помощью термопреобразователей сопротивления включает следующие составляющие:

Погрешность модуля ввода нормируется при условии, что сопротивление провода от модуля до датчика равно нулю. Поэтому эту составляющую погрешности можно рассчитать по форму­ле (9) и сложить с погрешностью модуля, но лучше откалибровать модуль с подключёнными к нему проводами нужной длины. ●

Литература