О некоторых особенностях формирования межчастотного корреляционного признака

В работах [1, 2, 3] показано, что для классификации отражённых сигналов обнаруженных объектов по их продольному размеру можно использовать характер флюктуаций отражённых сигналов на разных несущих частотах. В частности, в основе этого сигнального признака классификации лежит взаимосвязь значения нормированного межчастотного коэффициента корреляции с линейными размерами объекта: чем больше размер объекта, тем меньше межчастотный коэффициент корреляции.

Для того чтобы сформировать межчастотный коэффициент корреляции, используют наиболее эффективный алгоритм в виде оценки модуля максимального правдоподобия (ОМП) межчастотного коэффициента корреляции, которая выполняется в соответствии с формулой (1) [2].

Где  – оценка модуля межчастотного коэффициента корреляции, т.е. число накоплений по независимым выборкам наблюдения, например обзорам РЛС.

Z1_j = x1_j+ iy1_j , Z2_j = x2_j+ iy2_j в (1) – комплексные выборки классифицируемых эхо­сигналов на входе в двух частотных каналах. Квадратурные компоненты классифицируемых флюктуирующих сигналов имеют нормальное распределение, при этом без уменьшения общности подхода, так как данный алгоритм нечувствителен к изменению мощности сигналов мешающих отражений, дисперсия их равняется единице и среднее – нулю.

Решение о том, что классифицируемый объект протяжённый принимается, если (2).

Проиллюстрируем работу предлагаемого способа на конкретном примере, прибегнув как к аналитическому расчёту, так и к моделированию с помощью системы MATLAB [4].

Осуществим классификацию протяжённого объекта, используя две выборки наблюдений с межчастотным коэффициентом корреляции, равным 0. Корреляционный порог в расчётах будем менять от 0,1 до 0,9. Независимое число накоплений N возьмём равным 8 и 16.

Для нахождения вероятности правильной классификации протяжённого объекта по непревышению оценкой порога нужно воспользоваться распределением Уишарта. В работе [3] получено распределение (3), где Г() – гамма функция.

Для протяжённых объектов с = 0 и распределение (3) можно представить в более простом виде (4).

Используя (4), можно получить формулу для вероятности правильной классификации протяжённых объектов как вероятность непревышения   порога (5).

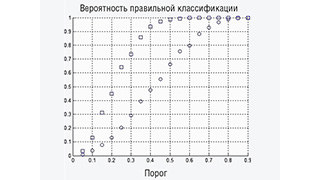
Для верификации данной формулы было проведено моделирование с помощью системы MATLAB [4] классификатора ОМП с расчётом для разных значений порога R_пор и N =16 и 32 (см. рис. 1 и 2 соответственно).

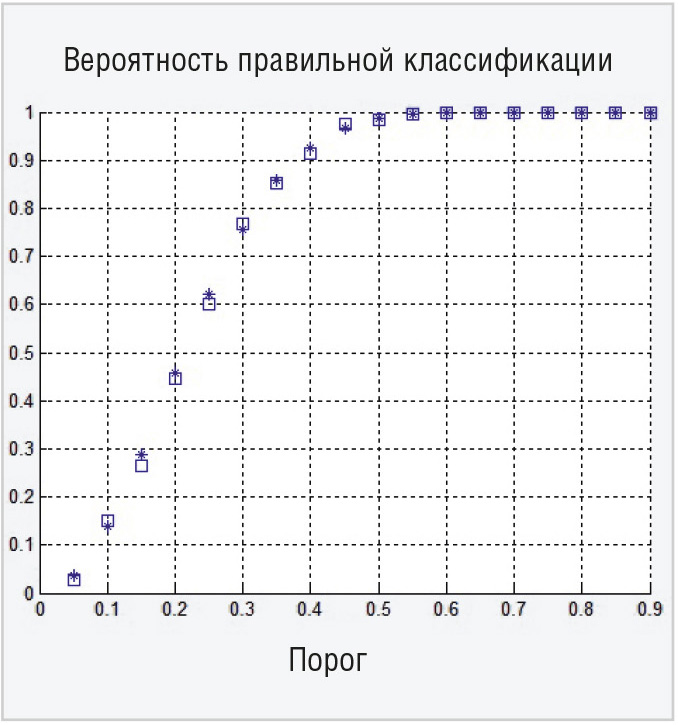
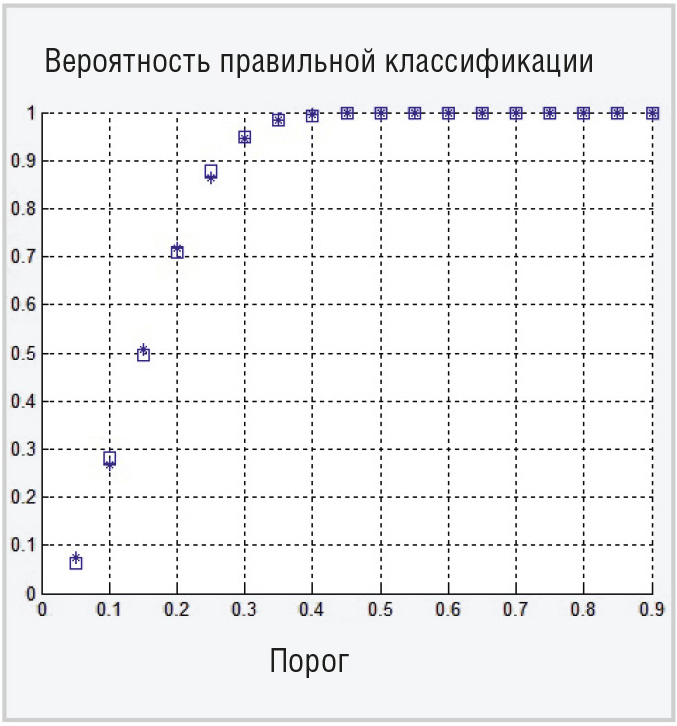
Результаты моделирования хорошо совпадают с аналитическими расчётами (см. рис. 1 и 2).

Все вышеприведённые исследования выполнены для независимых выборок наблюдений и получены, например, принимая отражённые сигналы от обзора к обзору РЛС. Однако представляет интерес и другой способ формирования модуля межчастотного коэффициента корреляции, когда обрабатываются сигналы в виде коррелированной пачки импульсов на каждой частоте в одном обзоре.

К сожалению, аналитически рассчитать вероятность правильной классификации протяжённого объекта в этом случае не представляется возможным, и результаты были получены только моделированием в MATLAB. Для этого использовалась модель отражённых сигналов на каждой частоте в виде коррелированной пачки импульсов с нормально распределёнными квадратурными составляющими и имеющих корреляционную функцию гауссовой формы. Межпериодный коэффициент корреляции задавался 0,7 и 0,9, для числа импульсов в пачке – 16 и 32. Результаты моделирования представлены на рис. 3–6.

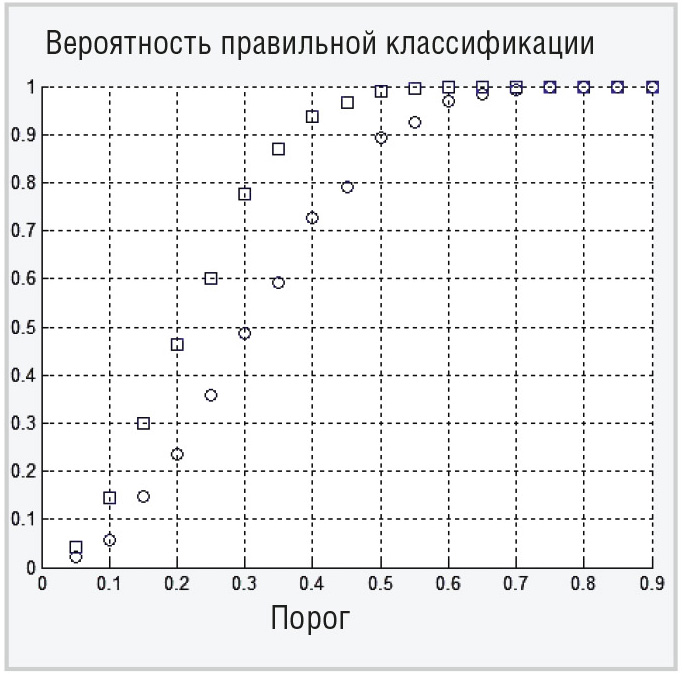
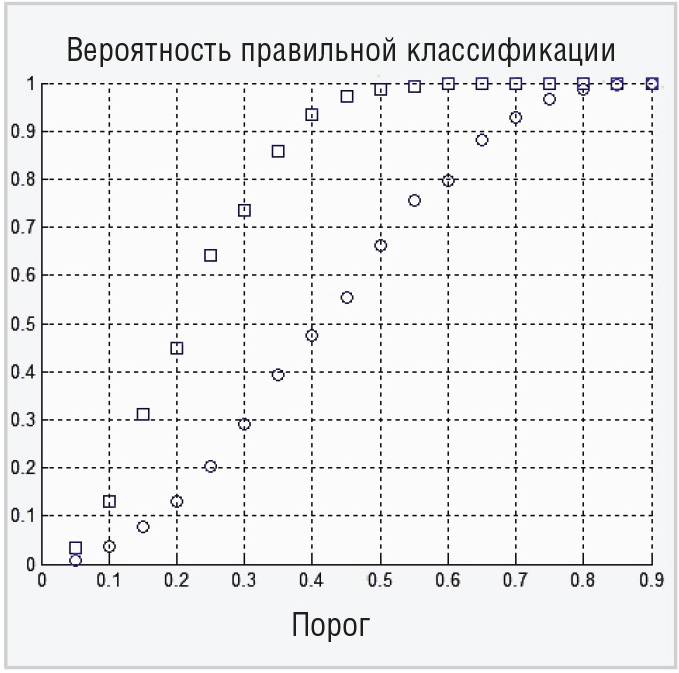
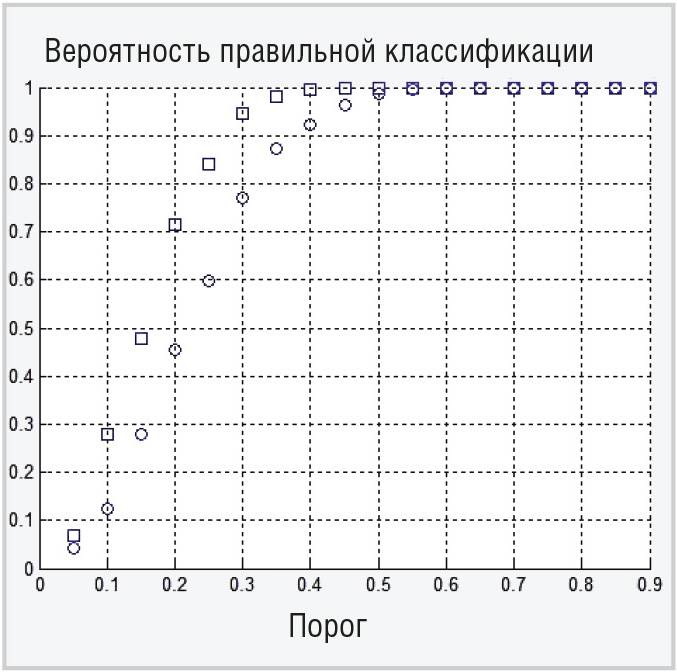
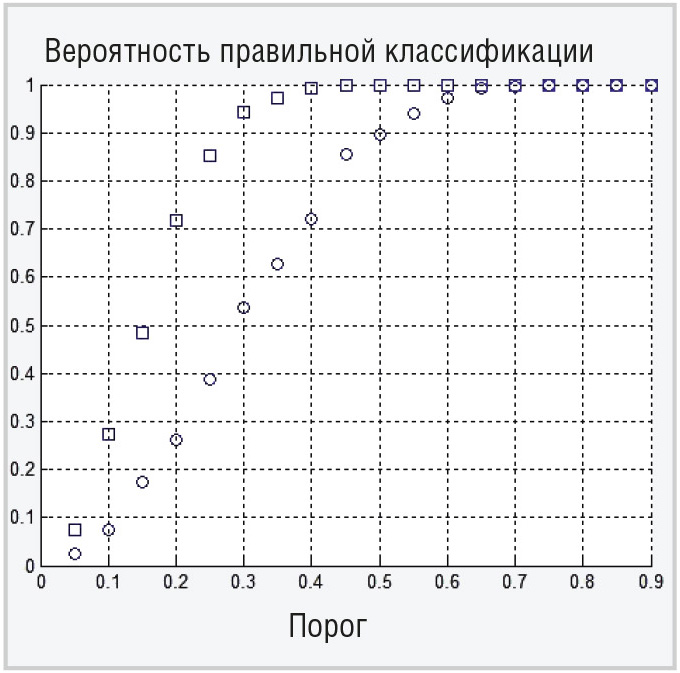
Таким образом, проведённое исследование полностью подтверждает положительный эффект от применения предложенного способа для классификации протяжённых объектов с использованием межчастотного корреляционного признака. Например, для независимых выборок наблюдения при N=16 для порога, равного 0,5, обеспечивается вероятность правильной классификации 0,99. Коррелированность же выборок наблюдения заметно снижает эффективность классификации. Так, при тех же 16 выборках наблюдений, но коррелированных с межпериодным коэффициентом корреляции 0,7, вероятность правильной классификации для порога 0,5 равна 0,9, а для межпериодного коэффициента корреляции 0,9 – около 0,7. Повысить эффективность классификации для коррелированных выборок можно или их декорреляцией, или увеличением их числа. Так для 32 коррелированных выборок с межпериодным коэффициентом корреляции 0,9 вероятность правильной классификации для порога 0,5 равна 0,9.

Литература

Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!