Радиолокационные обнаружители движущихся целей нового поколения

Введение

История борьбы с пассивными помехами в радиолокации насчитывает уже более 70 лет [1]. Однако до настоящего времени многие проблемы, связанные с этой задачей, не только не решены, но и ещё более усугубились. Технологии создания и постановки пассивных помех непрерывно совершенствуются. Кроме того, появление малоразмерных беспилотных летательных аппаратов, а также использование технологии Стелс (Stealth) при создании самолётов и крылатых ракет, имеющих малую эффективную площадь рассеивания (ЭПР), соизмеримую с ЭПР объектов, известных как «ангелы», создающих мешающие отражения от «ясного неба», приводит к снижению эффективности традиционных фильтровых адаптивных систем селекции движущихся целей (СДЦ). Всё это актуализирует исследования по разработке эффективных методов и алгоритмов обнаружения целей с малыми ЭПР на фоне целой совокупности многокомпонентных, в том числе и дискретных пассивных, помех [2]. Фактически, в данной отрасли стоит вопрос об использовании обнаружителей движущихся целей (ОДЦ), представляющих собой целый комплекс устройств фильтрации, стабилизации ложных тревог, адаптивного обнаружения и классификации принимаемых сигналов, превысивших порог обнаружения. Появление совершенной элементной базы в виде многоразрядных быстродействующих АЦП, высокопроизводительных многоядерных сигнальных процессоров (DSP), систем на кристалле (SOC) и программируемых логических интегральных микросхем с числом вентилей свыше нескольких миллионов (FPGA) открывает новые возможности для реализации более эффективных систем селекции движущихся целей. О двух таких высокоэффективных устройствах, входящих в обнаружитель движущихся целей, и пойдёт речь в данной статье.

Обнаружение сигналов движущихся помех на фоне многокомпонентных протяжённых пассивных помех

В практике защиты РЛС от сигналов многокомпонентных пассивных помех, вызванных совокупностью отражений от местных предметов, облаков, гидрометеоров, дипольных помех, применяют различные способы обнаружения полезных целей.

Один из способов обнаружения сигналов на фоне пассивных помех основан на предварительной адаптивной фильтрации пассивной помехи при помощи соответствующего выбора весовых коэффициентов фильтра [3] с последующим сравнением огибающей выходного сигнала с порогом. Основным недостатком этого способа является его низкая эффективность, обусловленная использованием фиксированных весовых коэффициентов для фильтрации сигналов, имеющих доплеровское смещение спектра. Кроме того, отсутствие нормирования сигнала до сравнения с порогом приводит к отсутствию стабилизации ложных тревог.

Известен способ обнаружения сигналов на фоне пассивных помех [4], который включает в себя: многоканальное весовое когерентное накопление, последующее выделение огибающих, адаптивную нормировку огибающих сигналов в каждом из каналов и их объединение. Тем самым формируется выходной сигнал, сравниваемый с порогом обнаружения. Недостатком данного способа является низкая эффективность защиты от пассивных помех за счёт того, что формирование вида частотных характеристик при весовом когерентном накоплении осуществляется без учёта таких параметров, как ширина спектра флуктуаций пассивной помехи и доплеровское смещение её частоты. Использование во всех каналах одинаковой весовой функции для уменьшения уровня боковых лепестков частотных характеристик каналов обеспечивает симметричное и равномерное подавление всех боковых лепестков фильтров, тогда как при оптимальной обработке осуществляется максимизация отношения сигнал/помеха за счёт разной коррекции частотных характеристик фильтров в зоне спектра флуктуации сигналов пассивной помехи.

Наиболее близким технически к рассматриваемому способу является патент США [5], в котором обработка строится следующим образом. На входе отражённые сигналы, представленные своими цифровыми квадратурными составляющими, подвергаются многоканальной доплеровской фильтрации и многоканальному когерентному накоплению в процессоре дискретного преобразования Фурье (ДПФ). На выходе процессора вычисляются огибающие, которые нормируются, объединяются и подаются на порог обнаружения, причём вычисление весовых коэффициентов для многоканальной доплеровской фильтрации осуществляется предварительно по приближённой формуле для выбранной заранее формы спектра флуктуаций пассивной помехи. В данном способе коррекция частотных характеристик при многоканальной доплеровской фильтрации производится более эффективно, с учётом близкой к реальности пассивной помехи, имеющей, например, гауссовский спектр. Для этого весовые коэффициенты, обеспечивающие оптимизацию частотных характеристик, предварительно рассчитываются по формуле [5]:

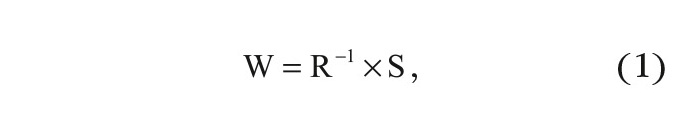
где R^–1 – обратная корреляционная матрица для предварительно заданной модели пассивной помехи, хранящаяся в постоянном запоминающем устройстве, S – вектор полезного сигнала, который для цели с неизвестной скоростью формируется в виде коэффициентов Фурье:

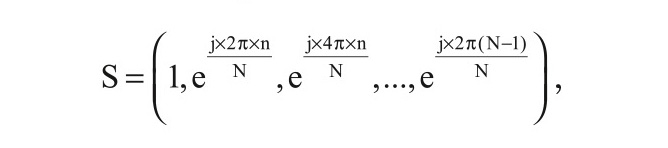
где n – номер доплеровского канала, а N – число импульсов в пачке.

В данном способе вычисление весовых коэффициентов, в силу невозможности в реальном времени оценить многомерную комплексную корреляционную матрицу и сделать её обращение, использован упрощённый подход. Суть этого подхода заключается в рассмотрении модели пассивной помехи, например, с гауссовой формой спектра и расчёте весовых коэффициентов без оценки и обращения всей корреляционной матрицы в реальном времени. Вместо этого производится только оценка модуля межпериодного коэффициента корреляции и его аргумента – межпериодного доплеровского набега фазы помехи. Затем на их основе из запоминающего устройства выбираются заранее рассчитанные весовые коэффициенты для неподвижной пассивной помехи, которые корректируются с учётом оценки межпериодного доплеровского набега фазы. К сожалению, заранее всё многообразие форм спектра предусмотреть невозможно, особенно если пассивная помеха многокомпонентная, то есть имеет многомодовый спектр одновременно отражённых сигналов от местных предметов, гидрометеоров и дипольных отражателей. Отсюда и низкая эффективность данного способа.

Для того чтобы повысить эффективность защиты РЛС от пассивных помех с многомодовыми спектрами, предлагается рассчитывать весовые коэффициенты доплеровского фильтра по отражённым сигналам от многокомпонентной пассивной помехи, используя аппроксимацию реальной помехи процессом авторегрессии [6, 7]. Это позволит не производить оценку корреляционной матрицы и её обращение, а в реальном масштабе времени оценивать коэффициенты авторегрессии. Воспользуемся в нашем случае иным представлением формулы (1), не прибегая к оцениванию и обращению комплексной корреляционной матрицы. Обратную корреляционную матрицу для процесса авторегрессии можно представить в виде разложения на диагональную D, верхнюю и нижнюю треугольные матрицы коэффициентов авторегрессии А:

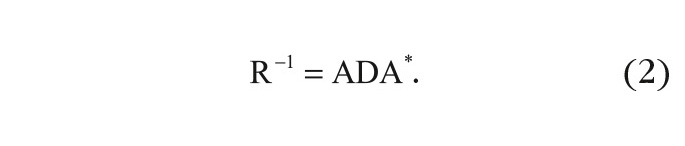
В соответствии с (2) получим:

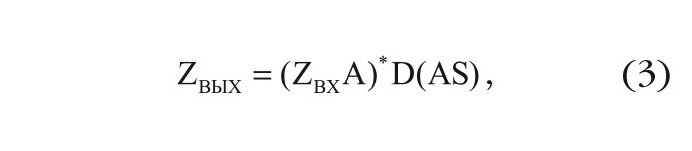
где Z_вх, Z_вых – комплексные сигналы, представляемые своими квадратурными составляющими на входе и выходе доплеровского фильтра, A – комплексный вектор коэффициентов авторегрессии. Левую часть формулы (3) в терминах патента метода-прототипа можно рассматривать как многоканальную доплеровскую фильтрацию, а правую – как когерентное многоканальное накопление в процессоре ДПФ. Диагональные члены D – это результат нормирования сигналов в каждом канале фильтра.

Преобразуем (3) так, чтобы совместить доплеровскую фильтрацию с когерентным накоплением сигналов цели с неизвестной скоростью:

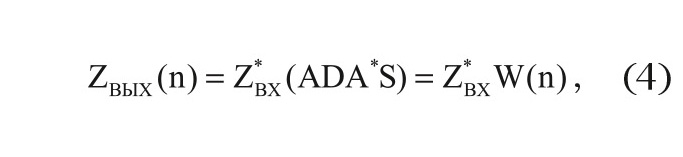
где n – номер доплеровского канала, N – число импульсов в пачке, а W(n) – вектор весовых коэффициентов для многоканальной доплеровской фильтрации, включающий в себя коэффициенты авторегрессии и коэффициенты Фурье.

В предлагаемом способе при неизвестной скорости цели адаптивная обработка реализуется с помощью многоканальной доплеровской фильтрации для каждого канала. Для каждого канала используются свои весовые коэффициенты, учитывающие как оценки коэффициентов авторегрессии, так и коэффициенты разложения по Фурье, что позволяет в отличие от метода-прототипа фильтровать сигналы пассивной помехи с многомодовыми спектрами.

Таким образом, в метод-прототип адаптивного обнаружения целей на фоне многокомпонентных пассивных помех, включающий в себя многоканальную доплеровскую фильтрацию, с многоканальным когерентным накоплением в виде дискретного преобразования Фурье, результат которого подвергается вычислению огибающих, которые нормируются и объединяются с выделением максимального значения, введены существенные изменения. Для операции многоканальной доплеровской фильтрации весовые коэффициенты теперь вычисляются в реальном времени посредством векторного перемножения оценённых коэффициентов авторегрессии и коэффициентов преобразования Фурье.

Такой подход обладает важнейшим преимуществом, поскольку без предварительного оценивания корреляционной матрицы помехи и её обращения, используя непосредственно выборку наблюдений, удаётся получать в реальном времени оценки коэффициентов авторегрессии с помощью эффективного в вычислительном отношении алгоритма. При этом с помощью ограниченного числа коэффициентов авторегрессии можно обеспечивать эффективное обнаружение целей для широкого класса многокомпонентных пассивных помех, имеющих многомодовые спектры. Наиболее предпочтительным из алгоритмов оценивания коэффициентов авторегрессии с точки зрения эффективности является алгоритм Берга [8, 9]. Ещё одна отличительная особенность предложенного способа состоит в обработке нескольких пачек импульсов на разных частотах повторения или на разных несущих частотах, что позволяет в целом улучшить скоростную характеристику работы обнаружителя сигналов по цели. Для этого при обработке каждой пачки из M сигнал, после отбора по максимуму каждой обработанной пачки импульсов, запоминается и по окончании последней обработанной пачки отбирается максимум от всех полученных максимумов. Он и сравнивается с порогом обнаружения:

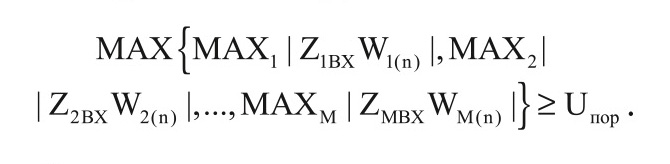
С целью исключения подавления полезного сигнала при фильтрации предлагается усреднять оценки коэффициентов авторегрессии по нескольким элементам дальности.

Выигрыш в эффективности предложенного способа по сравнению с прототипом оценивался в пороговом сигнале для вероятности правильного обнаружения 0,5 и вероятности ложной тревоги 10^–1–10^–2. Расчёт производился методом статистического моделирования в программе MATLAB. Пассивная помеха задавалась как двухкомпонентная помеха (с двухмодовым спектром), протяжённая по дальности. Первая мода имела относительную ширину спектра флуктуаций по уровню –20 дБ ΔF₁ / F_П = 0,15, вторая мода ΔF₂ / F_П = 0,25. Каждая мода имела превышение над шумом 20 дБ с относительным доплеровским смещением ΔF_Д1 / F_П = 0,35 и ΔF_Д2 / F_П = 0,5. Заданная скорость цели составляла 500 м/с. Число обрабатываемых импульсов – 12 (две пачки по 6 импульсов на двух частотах повторения 400 и 440 Гц.) Порядок авторегрессии – 5. Оценка коэффициентов авторегрессии производилась в MATLAB для первой SF11 и второй SF22 пачек (см. листинг 1).

Формирование весовых коэффициентов производилось векторным умножением оценок коэффициентов авторегрессии на коэффициенты Фурье (см. листинг 2).

На рисунке 1 показана частотная характеристика одного из каналов доплеровского фильтра, использующего оценки коэффициентов авторегрессии.

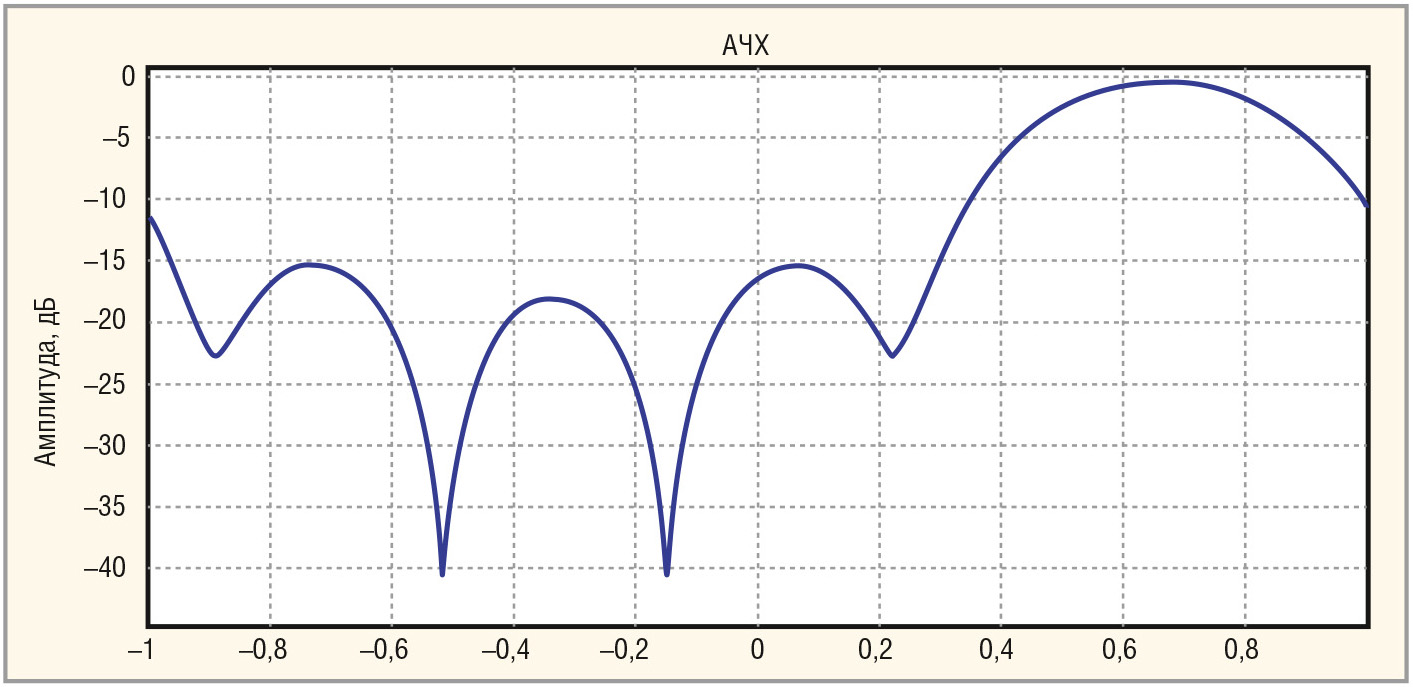
Хорошо просматриваются два глубоких провала для двух компонент пассивной помехи. Для прототипного способа оценка модуля межпериодного коэффициента корреляции и межпериодного доплеровского набега фазы также производилась в MATLAB (см. листинг 3).

Данные оценки, в предположении о гауссовой форме спектра помехи, использованы для воспроизведения корреляционных матриц помехи без доплеровского смещения для первой и второй пачек, которые затем обращаются с помощью программы inv MATLAB.

После поворота вектора входной выборки наблюдений на угол, соответствующий полученной оценке аргумента межпериодного коэффициента корреляции, производится многоканальная доплеровская фильтрация с весами, в которой используются воспроизведённые обратные матрицы RE1 для первой пачки и RE2 – для второй пачки (см. листинг 4).

Поскольку в описании метода-прототипа рассматривается обработка только одной пачки, сравнение предложенного способа с прототипом сначала производилось при обработке одной пачки, то есть когда выделенные огибающие на выходе доплеровских каналов после усреднения объединялись с отбором максимального значения с помощью функции max MATLAB, которое подавалось на порог обнаружения. Затем такое же сравнение было сделано при обработке двух пачек с разными двумя частотами повторения, с отбором в соответствии с формулой максимума при обработке каждой пачки.

Расчёты показали, что выигрыш в пороговом сигнале предложенного способа, по сравнению со способом, взятым в качестве прототипа, как при обработке одной пачки, так и для двух пачек, составляет 5–10 дБ. Объяснить полученную разницу в эффективности обнаружения достаточно просто, если сравнить корреляционные функции каждой из двух компонент пассивной помехи с корреляционной функцией, полученной по оценке результирующего модуля межпериодного коэффициента корреляции двухкомпонентной пассивной помехи (см. рис. 2).

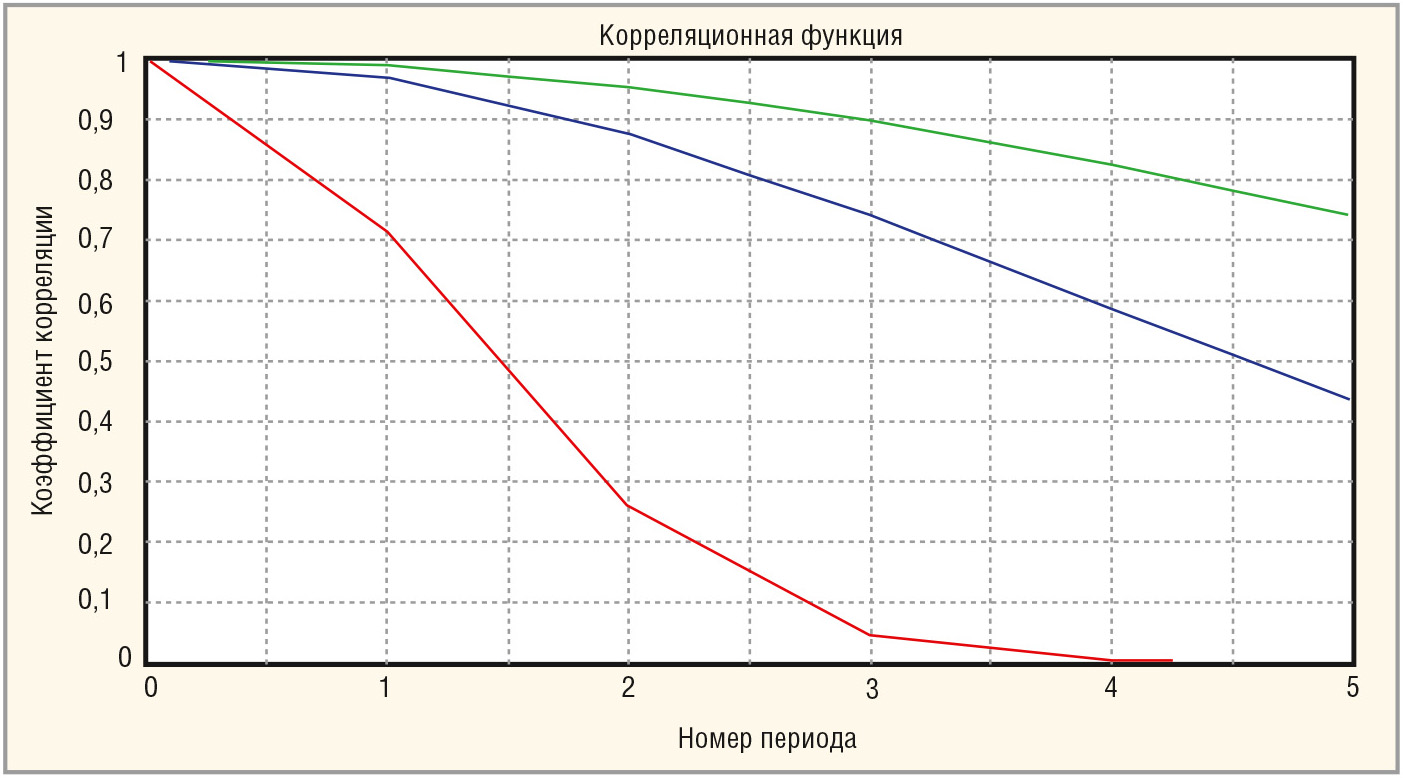
Кроме того, в исходном методе ошибочно формируется оценка межпериодного доплеровского набега фазы (аргумента межпериодного коэффициента корреляции) по двум доплеровски смещённым компонентам помехи. Поэтому оптимальные весовые коэффициенты в прототипе не соответствуют реальной помеховой обстановке, которую заранее не удаётся предусмотреть, даже сохранив в запоминающем устройстве огромное множество готовых весовых коэффициентов. Всё это приводит к снижению у прототипа эффективности обнаружения полезных целей на фоне многокомпонентных пассивных помех.

Обнаружение сигналов движущихся целей на фоне дискретных пассивных помех

В практике работы радиолокационных систем сантиметрового и дециметрового диапазонов волн отражения от «ясного неба» или, как их называют на Западе, «ангелы» известны достаточно давно. Эти мешающие радиолокационные отражения имеют различное происхождение, и их природа ещё не достаточно изучена. Иностранные учёные связывают это явление с эхо-сигналами от птиц (в особенности от стай перелётных птиц), скоплений насекомых (таких как, например, саранча), перемещающихся со скоростью ветра [10]. В отечественной литературе [11] происхождение эхо-сигналов от «ясного неба» объясняется появлением зон аномального распространения электромагнитных колебаний, в которых наблюдается интенсивные отражения на границе сред с различными показателями преломления, в том числе вызванных турбулентностями атмосферы – «термиками». Перелёты птиц происходят в одно и то же время суток (утром и вечером) и в определённые времена года. Соответствующие радио-локационные сигналы имеют характеристики, напоминающие эхо-сигналы от самолёта, поскольку высота полёта птиц может составлять 2 км, скорость от 20 до 150 км/ч, а ЭПР птиц в пределах импульсного объёма РЛС перелётных птиц составляет от 0,001 до 0,1 м², а в некоторых случаях достигает 1 м². Зоны аномального распространения радиоволн перемещаются со скоростью ветра и имеют высоту 2 км. ЭПР этих зон обычно меньше 1 м². Зоны образования эхо-сигналов имеют малое время жизни и их положение может существенно меняться от обзора к обзору РЛС. Размеры этих зон могут превышать импульсный объём РЛС и при увеличении высоты их интенсивность снижается. Существование «ангелов» в течение большей части года (с апреля по сентябрь), в том числе в период отсутствия массового перелёта птиц, позволяет считать, что основными источниками этих мешающих отражений являются не стаи птиц или рои насекомых.

Для повышения помехоустойчивости РЛС к воздействию отражений от «ангелов» в настоящее время используются следующие методы.

Рассмотрим методы классификации и бланкирования мешающих отражений более подробно. Известен способ классификации и бланкирования сигналов дискретных мешающих отражений, основанный на формировании так называемого скоростного порога, не превышение которого классифицируется как признак сигнала отражённого от мешающего точечного объекта с малой радиальной скоростью в данном элементе дальности [12]. Такой сигнал бланкируется, снижая поток ложных отметок на выходе приёмного тракта РЛС. Основным недостатком данного способа является его низкая эффективность, обусловленная необходимостью использования вобулированной пачки с ограниченным числом импульсов для однозначного измерения скорости. Кроме того, попытка выставления максимально высокого скоростного порога для повышения эффективности данного способа приводит к росту вероятности бланкирования полезных целей с малой радиальной скоростью. С технической стороны наиболее близким к заявляемому способу является двухчастотный способ классификации и бланкирования дискретных коррелированных помех. Данный способ строится на обработке отражённых сигналов на каждой несущей частоте РЛС в виде двух выборок наблюдения в каждом элементе дальности и включает в себя формирование оценок межпериодной доплеровской разности фаз с последующим их вычитанием для однозначного измерения скорости обнаруживаемого дискретного объекта [13]. Полученная таким образом оценка межчастотной межпериодной разности фазы сравнивается с фазовым порогом (фактически со скоростным порогом), на основании чего принимается решение о бланкировании отражённых сигналов от медленно движущихся мешающих точечных объектов, если этот порог оказался не превышен. Хотя данный способ позволяет осуществлять более эффективную классификацию сигналов, благодаря более высокой точности оценки межпериодной разности фазы на каждой несущей частоте РЛС, из-за отсутствия вобуляции периодов повторения с использованием большего числа импульсов, он недостаточно хорош для бланкирования полезных целей с малыми радиальными скоростями.

Для предотвращения бланкирования полезных сигналов от целей с малыми радиальными скоростями предлагается метод [14]. Этот метод предполагает, как и метод-прототип, на основе двух выборок наблюдений, принятых на двух несущих частотах, формирование оценок межчастотной межпериодной доплеровской разности фазы для однозначного измерения скорости объектов в каждом элементе дальности и сравнение этой оценки с порогом. При непревышении порога обнаруженный сигнал классифицируется по скоростному признаку как мешающий. Для мешающего сигнала дополнительно формируется модуль межчастотного коэффициента корреляции, который используется для оценки продольного размера классифицируемых объектов. При этом скоростному и корреляционному признаку для мешающих отражений ставят в соответствие логические единицы, совпадение которых фиксируют в каждом элементе дальности с помощью логической функции «И», на основании чего и принимается решение о бланкировании отражённого сигнала. При выборе разноса несущих частот в несколько процентов от частоты несущих руководствуются следующим:

Предлагаемый способ раскрывает новые функциональные возможности классификации и бланкирования дискретных помех и позволяет исключить бланкирование малоразмерных полезных целей, имеющих низкие радиальные скорости. Действительно, в способе, взятом в качестве прототипа, для однозначного измерения скорости обнаруженного объекта на каждой несущей частоте формируется оценка межпериодной доплеровской разности фаз с последующим формированием межчастотной межпериодной разности фаз. Для классификации объектов по скоростному признаку можно воспользоваться известной оценкой аргумента межпериодного коэффициента корреляции. Алгоритм этой оценки, получаемой по пачке из N-импульсов, может быть выражен в следующем виде:

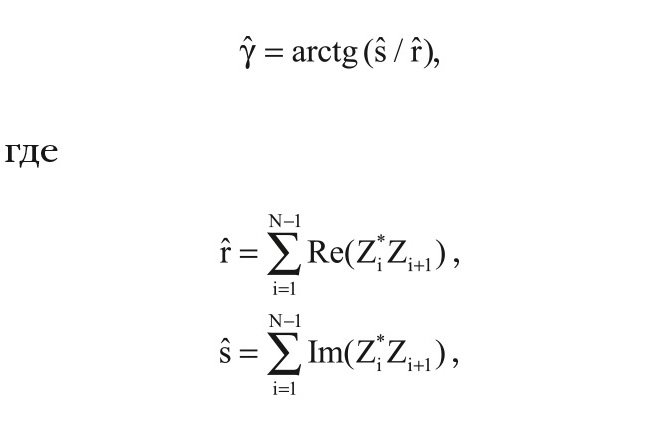
Z_i – комплексные выборки наблюдений на одной несущей частоте.

Классификация объектов по скоростному признаку может быть реализована с порогом γ_пор, соответствующим максимальной скорости движения мешающего объекта. Использование такого одночастотного алгоритма классификации сопряжено с существенным недостатком – наличием неоднозначности оценки доплеровской фазы. Известно, что оценка γ связана с длиной волны λ излучения РЛС, частотой повторения импульсов F и радиальной составляющей скорости полёта объекта V соотношением .

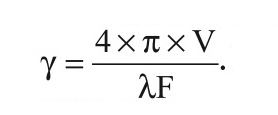
При относительно малых значениях частот повторения (F = 300–1000 Гц), которые используются в большинстве современных РЛС обнаружения, γ в несколько раз может превышать значение 2π даже в случае зондирования РЛС медленно движущегося объекта, в то время как функция арктангенса однозначно определена в интервале изменения фазы от 0 до 2π (или от –π до +π). Это может привести к увеличению вероятности ошибочной классификации скоростных и медленно движущихся объектов. Для устранения указанного недостатка в прототипе используются две несущих частоты РЛС. Доплеровский набег фазы на каждой из несущих частот можно представить в виде:

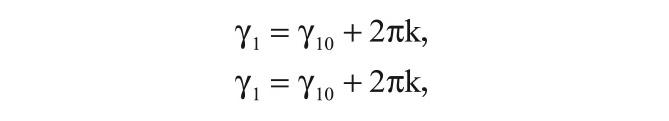
где γ₁₀, γ₂₀ – значения фазы в области определения (–π, +π), а k, n = 0, 1, 2, …, ∞.

Определим межчастотную разность фазы:

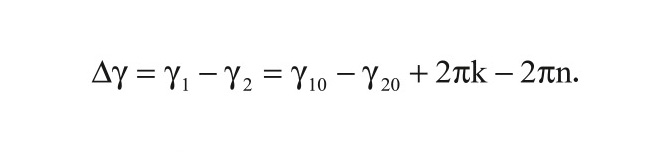
Для небольшого разноса несущих частот (несколько процентов от несущей) k = n получаем Δγ=γ₁-γ₂. Разность Δγ однозначно определена в пределах (–π, +π). Таким образом, алгоритм однозначного измерения разности фаз │ˆγ│:

Измеренная межчастотная разность межпериодной разности фаз сравнивается с порогом и, при непревышении порога, делается вывод о том, что отражённый сигнал происходит от точечных мешающих отражений и его необходимо бланкировать. Так в методе, взятом в качестве прототипа [13], использовалась оценка межчастотной межпериодной разности фаз. В предлагаемом же способе оценка межчастотной межпериодной разности фаз путём сравнения с порогом формирует лишь первый скоростной признак, например, в виде логической единицы, если порог не превышен.

Использование двух несущих частот для однозначного измерения скорости даёт возможность сформировать ещё один признак классифицируемого объекта – межчастотный коэффициент корреляции. Как показано в работе [15], для классификации отражённых сигналов от объектов по их продольному размеру можно использовать характер флуктуаций отражённых сигналов на разных несущих частотах. В частности, в основе второго признака классификации в предлагаемом способе лежит взаимосвязь значения нормированного межчастотного коэффициента корреляции с линейными размерами объекта. Чем больше размер объекта, тем меньше межчастотный коэффициент корреляции. Если разнос несущих частот выбрать из условия:

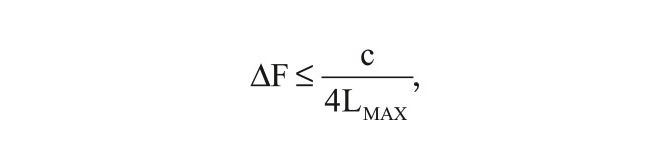
где L_MAX – максимальный разнос участков локального отражения вдоль линии визирования РЛС на объект при разных несущих частотах зондирующего сигнала, то величина межчастотного коэффициента корреляции R(ΔF) будет связана с размером объекта L выражением:

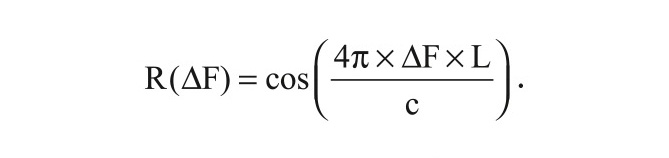
Как следует из этой формулы, для того чтобы отличить летательные аппараты с малым продольным размером от медленно перемещающихся дискретных мешающих объектов, имеющих значительно большие размеры L, достаточно выбрать разнос несущих частот ΔF порядка 10 МГц [15]. Современные летательные аппараты имеют максимальный размер менее 75 м, что значительно меньше разрешающей способности РЛС обнаружения, составляющей 150–300 м, то есть соизмеримой с размерами дискретных пассивных помех.

В этом случае для самого большого самолёта, например, Airbus A380, размером 72 м, межчастотный коэффициент корреляции равен:

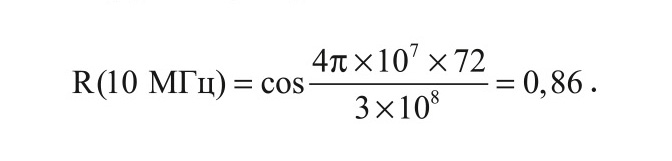
Для меньшего размера отечественного лайнера ИЛ-96-300 длиной в 55 м:

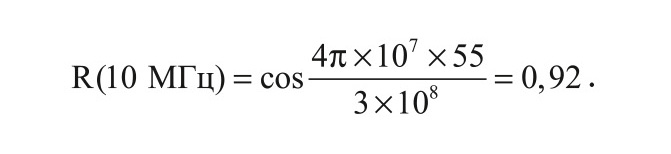
В то время как для 200-метрового мешающего объекта:

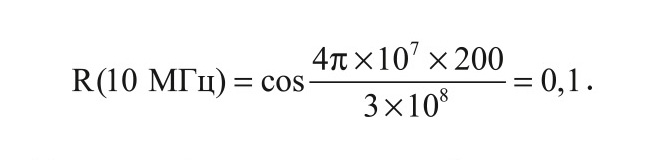
Таким образом, при выборе разноса несущих не более 10 МГц посредством сравнения корреляционного признака с пороговым значением формируется второй логический признак.

При наличии двух логических единиц (операция «И») принимается решение о бланкировании сигнала отражённого мешающим объектом в данном элементе дальности. Следует отметить, что разнос несущих в 10 МГц хорошо согласуется с требованием однозначной оценки и скоростного признака, то есть составляет несколько процентов от частоты несущих современных РЛС обзора.

Остаётся лишь решить, как формировать межчастотный коэффициент корреляции, выбрав для этого наиболее эффективный алгоритм оценки. Как и для первого скоростного признака, для формирования межчастотного коэффициента корреляции применим накопление оценки по пачке из N-импульсов:

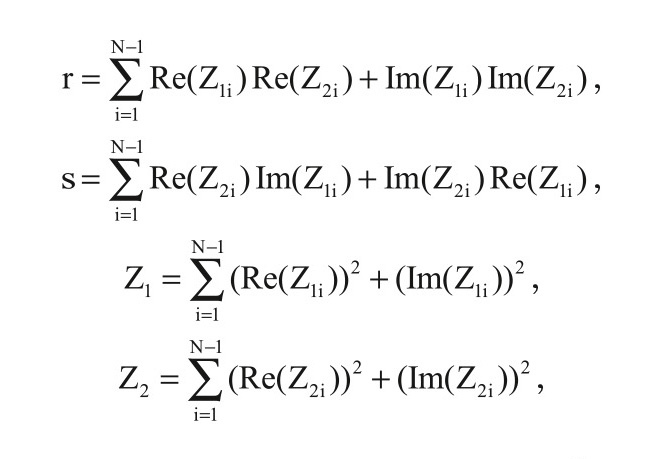
где z_1i и z_2i – комплексные выборки наблюдений на первой и второй несущей частоте. Тогда межчастотный коэффициент корреляции может быть вычислен по следующей формуле:

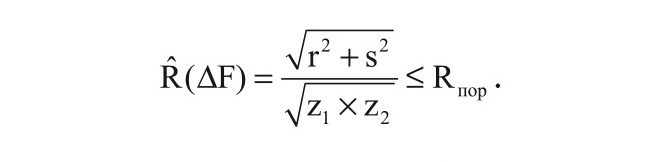
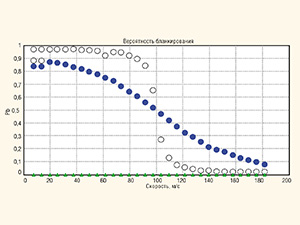
Проиллюстрируем работу предлагаемого способа на конкретном примере, прибегнув к моделированию с помощью системы MATLAB. Осуществим классификацию объекта, движущегося со скоростью от 10 до 180 м/с, используя две выборки наблюдений в виде двух пачек импульсов с постоянным периодом повторения 0,001 с, отражённых от объекта на разных несущих частотах: 500 и 510 МГц. Объект может иметь ширину спектра флуктуаций от нескольких герц до нескольких десятков герц и два разных продольных размера, характеризуемых двумя межчастотными коэффициентами корреляции 0,1 (мешающий объект) и 0,9 (полезный объект). Скоростной порог установлен в 100 м/с, а корреляционный порог – 0,5. Обрабатываемое число импульсов в пачке на каждой несущей равно 8.

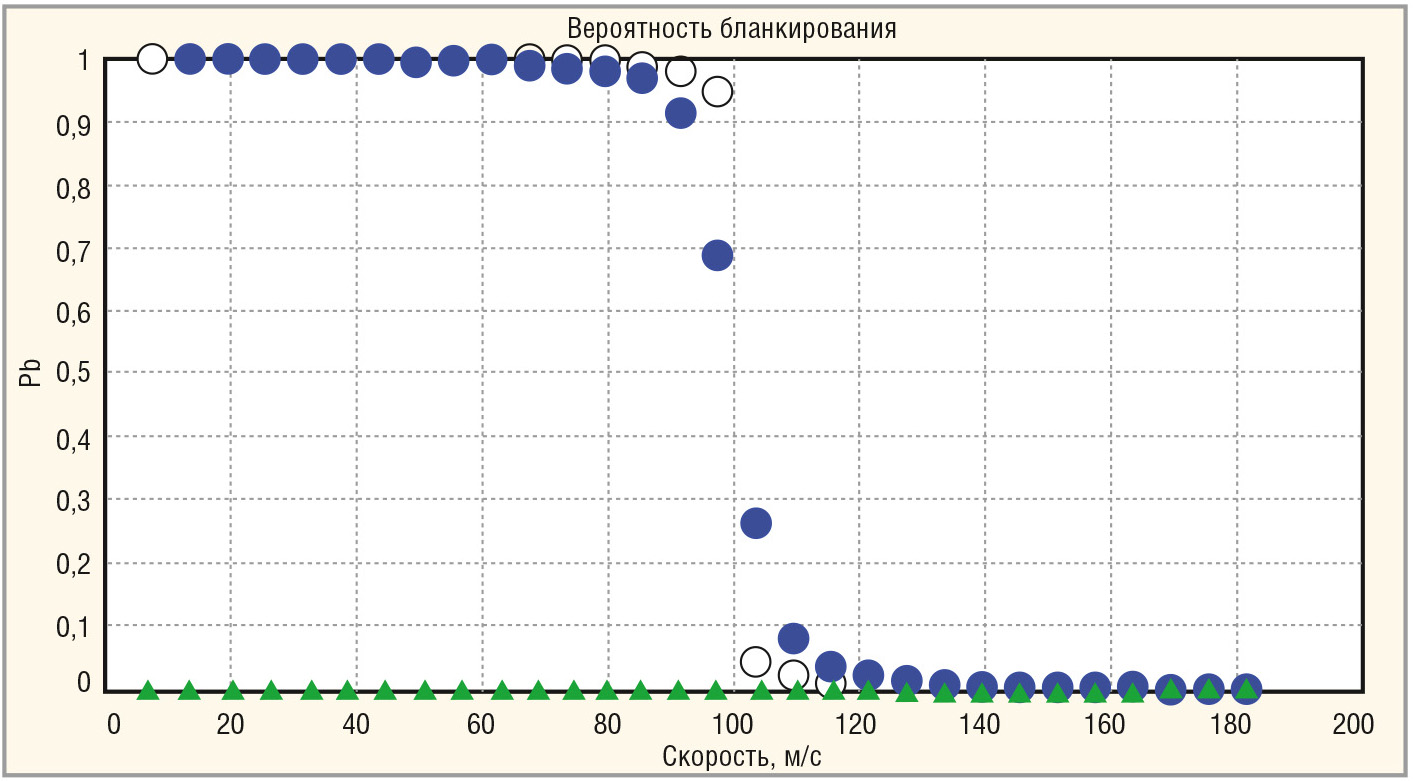
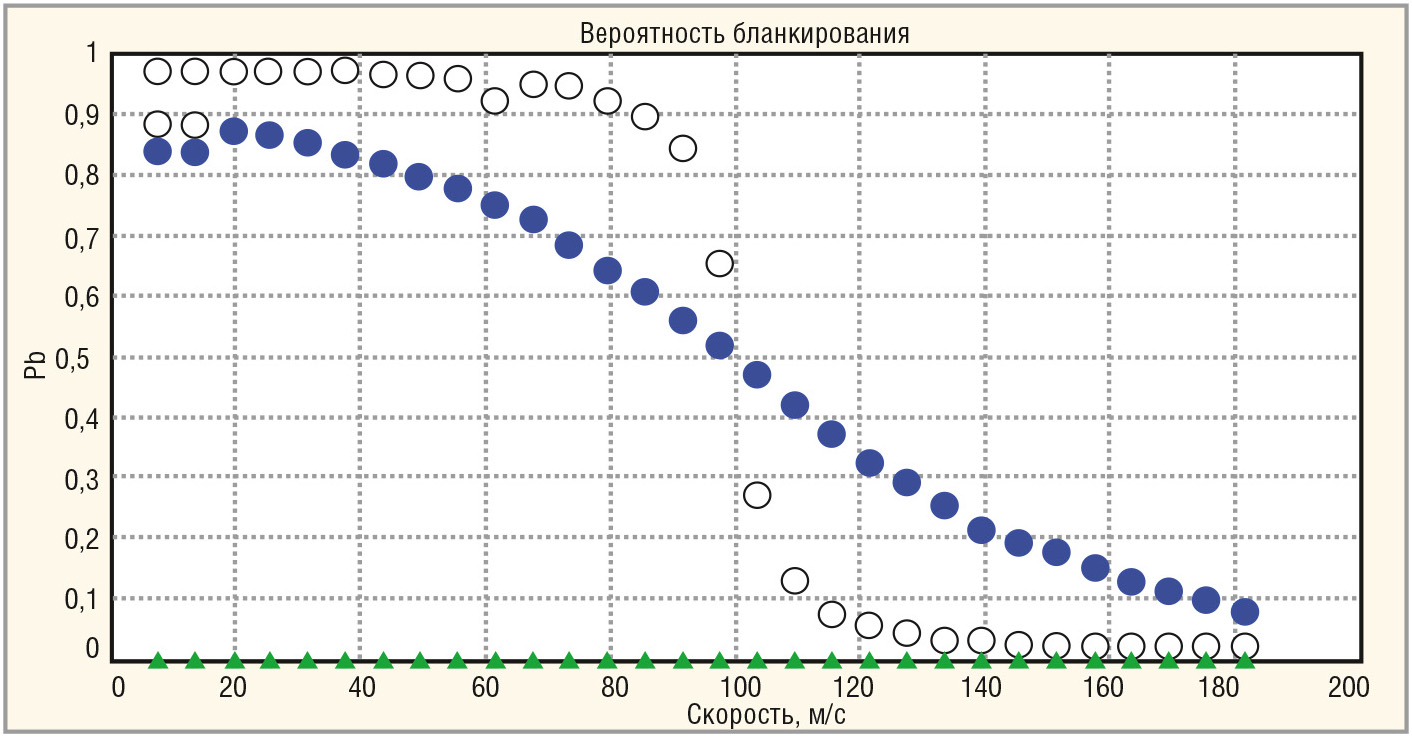
Примечание: ○ – метод-прототип, ▲ (объект 200 м) и ● (объект 50 м) – предложенный метод

Результаты моделирования вероятностей бланкирования данных объектов в MATLAB с использованием предложенного способа (отмечены треугольниками) и способа, взятого в качестве прототипа (отмечены кружками), представлены на рисунках 3 и 4. На рисунке 3 приведена вероятность бланкирования объектов с узким спектром флуктуаций. Для мешающего объекта с большим продольным размером (оценка межчастотного коэффициента корреляции не превысила порог 0,5) вероятности бланкирования обоих способов совпадают. Для малоразмерных целей у метода-прототипа бланкирование имеет место быть, даже если скорость объекта заметно превышает порог 100 м/с. У предложенного способа малоразмерные цели не бланкируются. На рисунке 4 показаны результаты для объекта с более широким спектром флуктуаций. Можно отметить главное отличие от предыдущих результатов (см. рис. 3) – размытость вероятности бланкирования на границе скоростного порога в 100 м/с и снижение вероятности бланкирования в области малых скоростей мешающих объектов. В целом же, и в этом случае, предложенный способ имеет явные преимущества перед известным ранее.

Таким образом, проведённое моделирование в системе MATLAB полностью подтверждает положительный эффект от применения предложенного способа классификации и бланкирования дискретных пассивных помех.

Заключение

Представленные два новых способа обнаружения и классификации пассивных помех разного типа не исчерпывают всех возможных способов повышения эффективности когерентной обработки сигналов в современных РЛС. Тем не менее, они отражают новую ступень в развитии средств защиты РЛС от пассивных помех в новых более сложных условиях априорной помеховой неопределённости.

Литература

1. Бакулев П.А., Бартенев В.Г., Григорьев Л.Н., Кобзарев Г.Ю. Разработка первых систем защиты РЛС от пассивных помех. Радиотехника. 2016. №5. С. 142–151.
2. Бартенев В.Г. Радиолокационные отражения от «ясного неба» вынуждают улучшать параметры РЛС. Современная электроника. 2014. №7. С. 18–20.
3. Бакулев П.А., Степин В.М. Методы и устройства селекции движущихся целей. М. Радио и связь. 1986.
4. Патент США №3831174 G01s 9|06. 1974.
5. Патент США №4742353 G01s 13|86. 1988.
6. Бартенев В.Г. Способ адаптивного обнаружения сигналов движущихся целей на фоне многокомпонентных пассивных помех. Патент РФ №2593146. По заявке №2015128480. Опубликован 27.07.2016. Бюл. №21.
7. Бакулев П.А., Кован С.Е. Алгоритм обнаружения сигналов на фоне многомодовых коррелированных помех. Радиотехника.1981. Т. 36. №8. С. 69–72.
8. Marple S.L. Digital Spectral Analysis. Englewood Cliffs. NJ: Prentice Hall. 1987. Chapter 7.
9. Бартенев В.Г., Кутепов В.Е. Сравнительный анализ двух способов формирования весовых коэффициентов в адаптивной системе селекции движущихся целей. Цифровая обработка сигналов. 2014. №2. С. 58–60.
10. Harper W.G. Detection of Bird Migration by Centimetric Radar – a Cause of Radar «Angels». Proceedings of the Royal Society of London. Series B. Biological Sciences. Volume 149. Issue 937. 1958. P. 484–502.
11. Черников А.А. Радиолокационные отражения от «ясного неба». Гидрометеоиздат. Л. 1979.
12. Бартенев В.Г. Дракин Е.В. Цифровая система СДЦ. Авторское свидетельство СССР №160231 по заявке №228451 от 13 августа 1980 г.
13. Бартенев В.Г., Галкин Р.Е. Синтез цифрового двухчастотного классификатора дискретных помех по скоростному признаку. Труды 16 Международной конференции «Цифровая обработка сигналов и её применение DSPA-2014». Москва. Т. 1. 2014. С. 343–347.
14. Бартенев В.Г. Способ классификации и бланкирования дискретных помех. Патент РФ №2599870 по заявке № 2015128907. Опубликован 20.10.2016. Бюл. №29.
15. Абраменков В.В., Климов С.А., Бондарев П.А., Юдин В.А., Гульшин В.А. Разрешение и распознавание радиолокационных объектов. Ульяновск. УлГТУ. 2012.