Математическая модель механической скорости проходки для оптимального управления бурением нефтегазовых скважин

Основным процессом при бурении скважин является разрушение породы долотом. Для его описания используется уравнение для механической скорости бурения υ_м. На величину скорости оказывают влияние многочисленные факторы: нагрузка на долото, крутящий момент на долоте, частота его вращения, расход и давление бурового раствора, реологические свойства раствора, литологические характеристики породы на забое и др. Однако на практике для управления скоростью проходки используется только осевая нагрузка на долото G, так как в ходе рейса остальные параметры принимаются неизменными.

М.Г. Бингхэм (США) подробно изучил функцию υ_м = f(G), где G – удельная (т.е. приведённая к забойной площади S_з = πD_δ²/4, D_δ­­ – диаметр долота) осевая нагрузка на долото по большому массиву промысловых и экспериментальных данных бурения [5]. Он пришёл к выводу, что эта функция является степенно́й и имеет форму S-образной кривой, приведённой на рис. 1. 

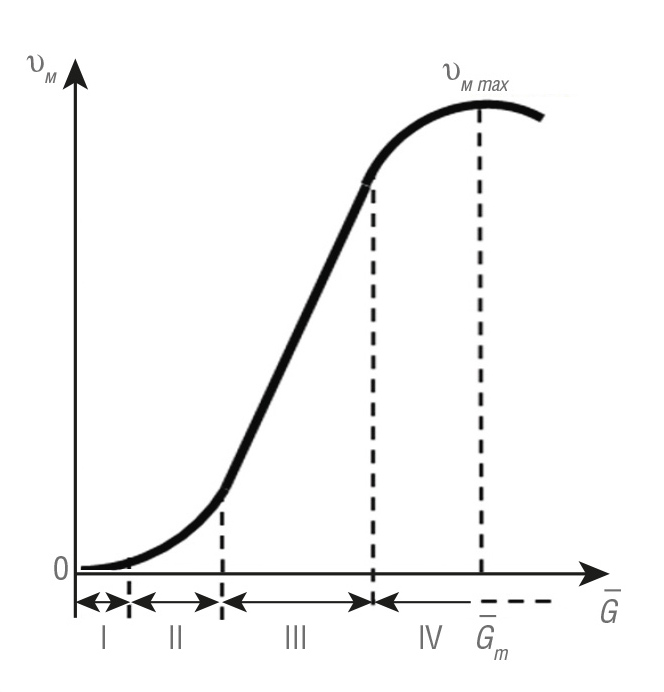
Качественная связь функции с физико-механическими свойствами проходимого пласта породы и параметрами промывочной жидкости также определена Бингхэмом. Отечественная и зарубежная практики бурения подтверждают эти выводы [1, 2, 4–6 и др.]. 

Согласно Бингхэму, функция скорости υ_м имеет несколько зон:

• l зона I – осевые нагрузки малы, разрушение породы несущественное, в виде поверхностного истирания, давление зубьев долота на породу меньше предела её прочности; 
• l зона II – контактное давление зубьев долота на забой возрастает, от породы откалываются небольшие кусочки, что приводит к заметному росту υ_м по нелинейному закону степенно́го вида;
• l зона III – нагрузка G становится больше, чем предел прочности породы, это приводит к значительному объёмному разрушению породы по закону, близкому к линейному, но с наклоном, существенно бо́льшим, чем в зоне I;
• l зона IV – характеризуется тем, что промывочная жидкость не успевает выносить выбуренную породу на поверхность, шлам оседает на забой и повторно перемалывается. При этом значение υ_м становится максимальным при осевой нагрузке G_m и затем уменьшается.

Для описания процесса разрушения породы разработано множество математических моделей скорости проходки, как отечественных, так и зарубежных. Основными и наиболее характерными из них являются следующие.

Модель ВНИИБТ имеет интегральный вид [6], получена в результате отработки большого количества шарошечных долот и предназначена для использования при бурении с верхним приводом и при роторном бурении:
υ_м = k_δG^δn^α,
где k_δ – коэффициент буримости породы, зависит от типа долота, свойств породы и раствора; n – частота вращения долота, об/мин; δ, α – показатели, задающие крутизну кривой.

Модель Погарского А.А. [6] для скорости υм содержит коэффициент b, позволяющий в неявном виде учитывать влияние на скорость гидравлического параметра – расхода промывочного раствора:

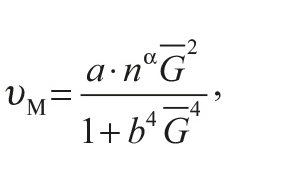
где a – коэффициент буримости; α – показатель, влияющий на крутизну кривой; b – коэффициент, зависящий от расхода раствора.

Модель фирмы «Теннеко ойл комп»
[5, 6] связывает механическую скорость с нагрузкой на долото, частотой его вращения, учитывает типоразмер долота, параметры породы и промывочного раствора:

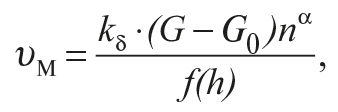
где G₀ – критическая нагрузка на долото, обеспечивающая внедрение зубьев в породу; f(h) – функция, характеризующая состояние долота.

Модель Галле-Вудса-Лубинского [5, 6] имеет дифференциальный вид, описывает мгновенное состояние процесса углубления скважины в любой момент времени, что задаётся трёхмерным вектором в пространстве состояний с координатами: мгновенные скорость υ_м, износ зубьев и износ опоры долота.

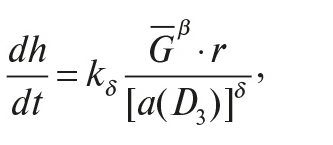
где β – показатель степени при осевой нагрузке; r – функция, зависящая от оборотов n и рассчитываемая отдельно для пород разной твёрдости; а(D₃) – функции износа вооружения долота; D₃ – степень относительного износа вооружения долота; δ – показатель степени для функции а(D₃).

Расчёты по этим моделям показали, что формы кривой υ_м = f(G) для них имеют вид, приведённый на рис. 2.

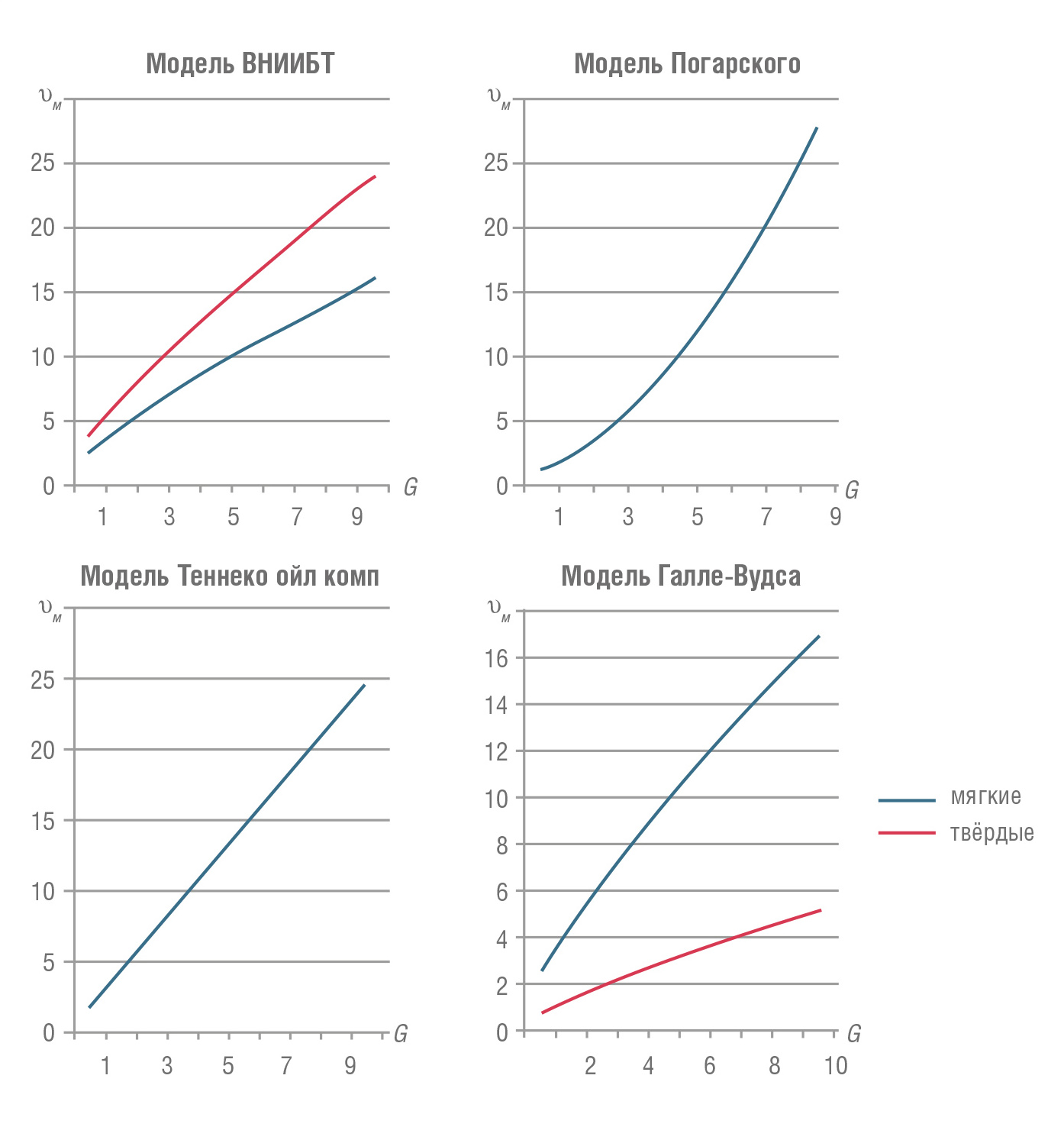
Анализ показывает, что модели с различной степенью точности описывают работу долота только на участках I–III кривой М.Г. Бингхэма, максимума не имеют, поэтому для оптимизации непригодны.

Как уравнение регрессии, кривая М.Г. Бингхэма может быть представлена фрагментом синусоиды, сдвинутой в первый квадрант координатной плоскости (рис. 3). 

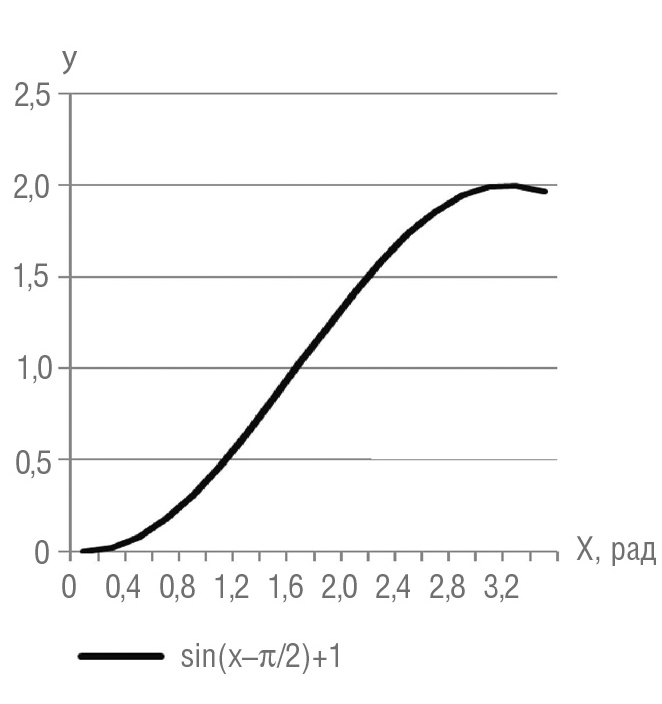
Поэтому для  оптимального управления бурением разработана математическая модель υ_м = f(G) как приближающая функция в виде участка синусоиды, представленной рядом Маклорена. 

Ряд Маклорена для функции «синус» является бесконечным разложением и имеет вид:


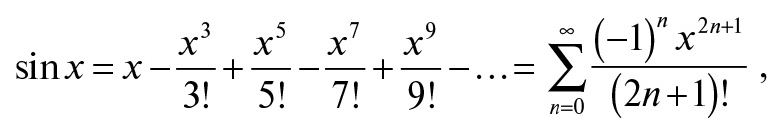
однако для математической модели механической скорости достаточно взять несколько первых членов ряда, количество которых обеспечивает требуемую степень аппроксимации модели к реальным условиям бурения в скважине.

На рис. 4 приведены графики ряда Маклорена, содержащие от двух до пяти членов ряда и график синусоиды, которые показывают, что до экстремума все линии практически совпадают друг с другом, для кривой, построенной по двум первым членам ряда, максимум находится ниже и левее максимума синусоиды, у кривых для 3, 4, 5 членов и синусоиды экстремумы находятся в одной точке, но после него кривая для 3 членов идёт несколько выше, чем остальные кривые. 

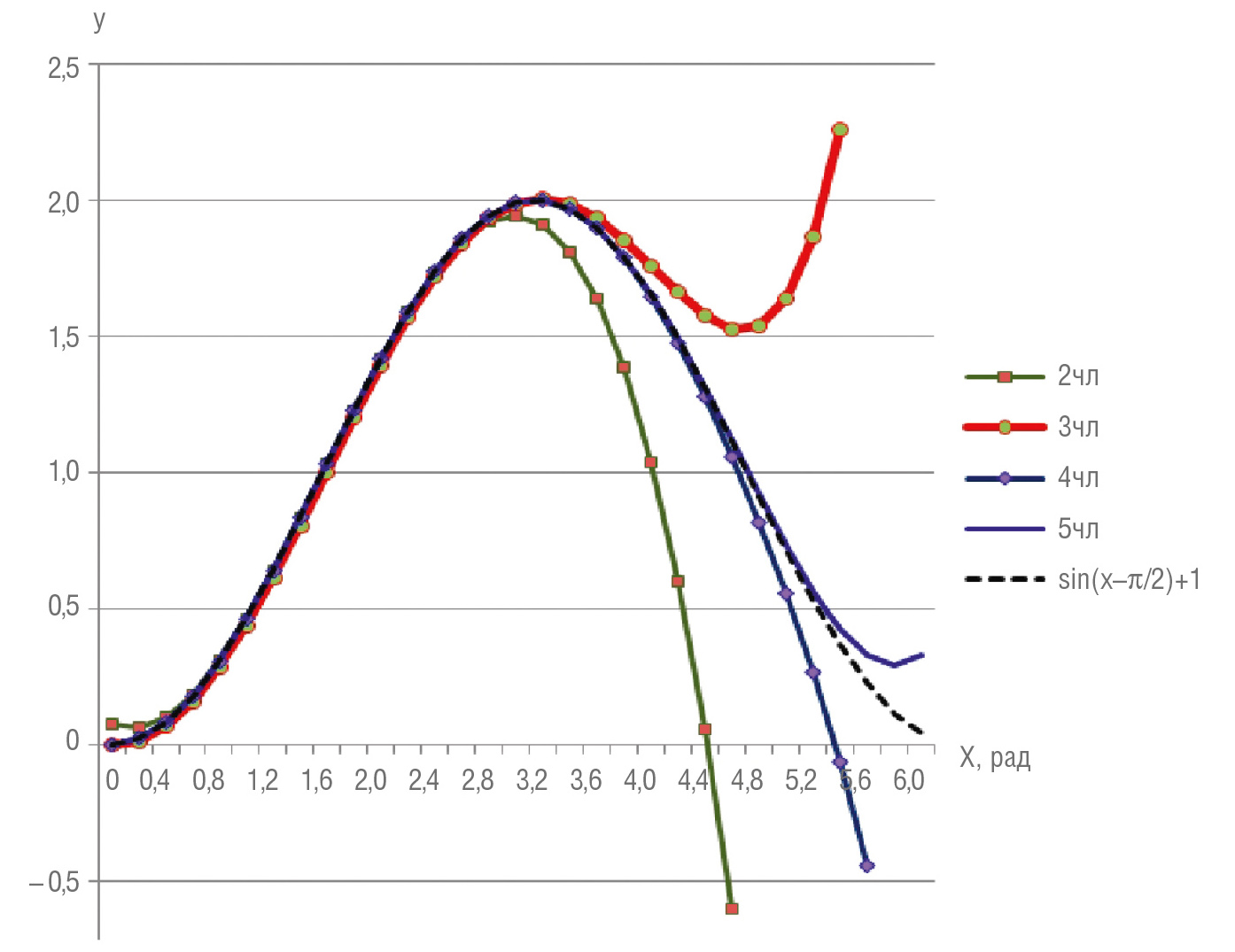
Однако при экстремальном управлении приближение к точке максимума обычно происходит слева, поэтому до экстремума форма кривой должна точно описывать оптимизируемый процесс, а после максимума степень уменьшения функции не очень существенна и может не строго соответствовать процессу, поэтому для аппроксимации функции М.Г. Бингхэма достаточно взять уравнение, состоящее из трёх членов ряда (чтобы не перегружать модель механической скорости лишними составляющими):

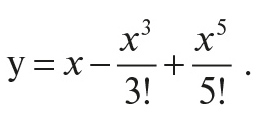
Для перемещения выделенного фрагмента синусоиды в первый квадрант нужно поднять график на 1 по оси у и сдвинуть его влево на 1,57 рад по оси х. После замены факториалов их численными значениями получим:

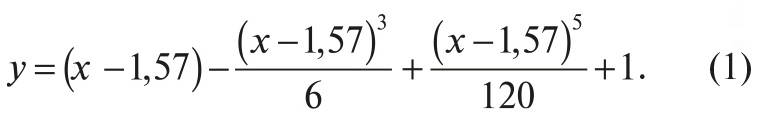
При рабочих режимах бурения, в зависимости от мощности бурового станка и глубины скважины, осевая нагрузка на долото G изменяется в пределах от 0 до 40 Н, а величина скорости бурения может достигать 10…14 м/ч и выше [1, 2, 6], поэтому для соответствия аргумента х величинам нагрузки на долото G, а функции у – реальной скорости бурения υ_м их нужно перемасштабировать, для чего ввести в формулу (1) соответствующие коэффициенты: 

• для преобразования радианной меры измерения аргумента х в единицы измерения нагрузки на долото G [Н] значения х нужно разделить на некоторую константу С_G;
• для растяжения функции у по вертикали нужно выражение (1) умножить на коэффициент пропорциональности k.

В результате модель для оптимизации скорости проходки примет окончательный вид:

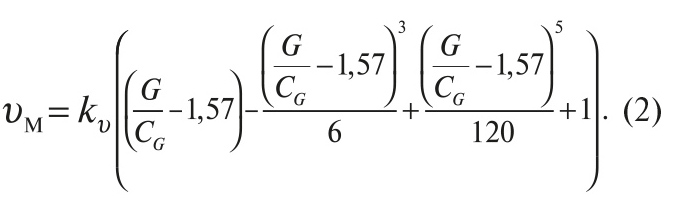
Для проверки достоверности полученной модели и её адекватности реальным условиям бурения использованы данные буровых рапортов по законченным в Краснодарском крае скважинам Восточно-Прибрежная № 9, Песчаная № 7 и Крупская № 1. Средняя погрешность экспериментальных данных и данных, определённых по модели (2), составила 28%, 12% и 13% соответственно.

Рассчитанная по модели (2) кривая скорости проходки и опытные данные проводки этих скважин показаны на рис. 5. 

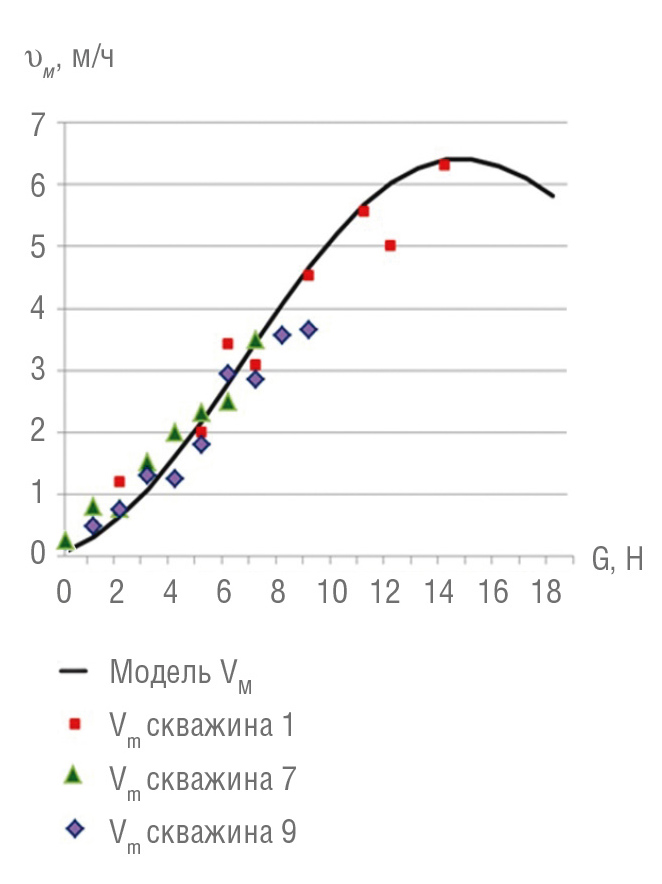
В результате можно сделать следующие выводы.

Данные пробуренных скважин подтверждают, что модель бурения (2) достаточно точно, со средними погрешностями 12…28% описывает процесс механического разрушения породы. При этом следует учитывать причину отклонения опытных данных от аналитических: оно связано с тем, что бурение скважин проводилось на параметрах, рекомендованных проектами по результатам проводки соседних скважин, но они практически не являются оптимальными для данной скважины.

В ходе бурения были достигнуты оптимальные режимы, но только для отдельных интервалов глубины, в основном для скважины № 1. 

Опытные и модельные данные подтверждают, что кривая М.Г. Бингхэма имеет S-образную форму.

Оценка адекватности модели

В публикации [4] рекомендуется использовать общепринятые статистические критерии для оценки адекватности и качества созданных математических моделей, которые позволяют быстро оценивать их основные параметры. Рекомендации разработаны применительно к транспортным сетям, но, так как статистические критерии являются универсальными, они могут быть применены к моделям любых процессов и объектов.

Для оценки моделей использовались пять показателей: 

• абсолютная средняя ошибка δ_a;
• относительная средняя ошибка δp; 
• отклонение среднеквадратическое υ_a;
• относительное отклонение средне-квадратическое υ_p;
• коэффициент корреляции r.

Определим значения критериев для новой модели (табл. 1).

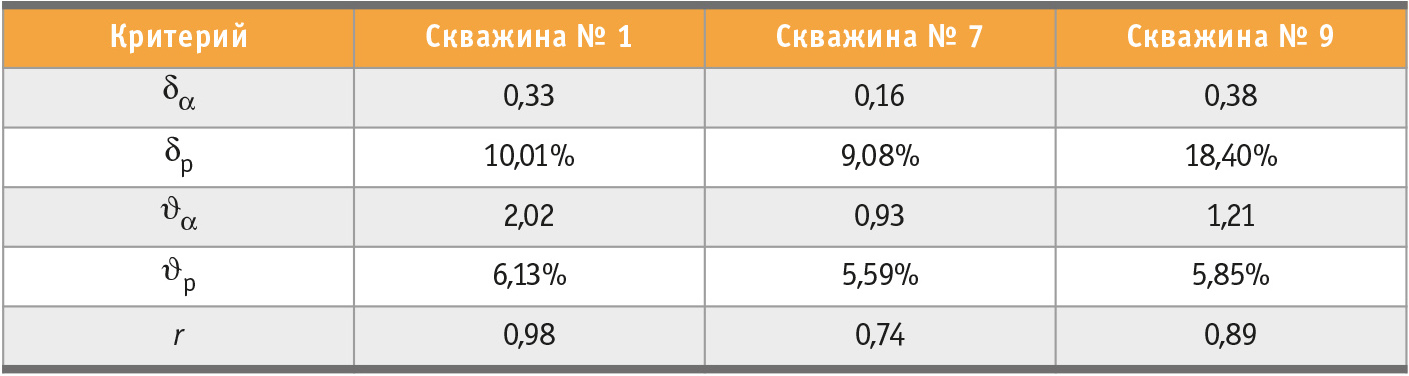
В настоящее время пока не выработаны чёткие значения этих критериев, при которых модель считается достоверной, но для практического применения в публикации [4] рекомендовано, что относительные показатели не должны быть более 10%, а коэффициент корреляции не должен быть менее 0,9.

Результаты показывают, что модель хорошо коррелируется с буровыми процессами и пригодна для управления оптимальной проводкой скважин, коэффициент корреляции модели с буровыми данными близок к 1.

Основные выводы и результаты

1. Анализ основных известных моделей бурения показал, что они используют только линейный участок кривой М.Г. Бингхэма, экстремума не имеют, поэтому к оптимизации и применению в ИБА непригодны.
2. Новая модель бурения представлена тремя членами разложения функции «синус» в ряд Маклорена, имеет экстремум, её достоверность подтверждена результатами пробуренных скважин, коэффициент корреляции модели с буровыми данными близок к 1.
3. Экспериментальные буровые данные подтверждают, что модель механической скорости пригодна для управления оптимальной проводкой скважин, коэффициент корреляции модели с буровыми данными близок к 1. ●

Литература

1. Мусанов А.М. Техника и технология бурения нефтегазовых скважин: учебник. М.: Фолиант, 2017. 222 с.
2. Григулецкий В.Г. Оптимальное управление при бурении скважин. М.: Недра, 1988. 227 с.
3. Методические рекомендации по разработке и реализации мероприятий по организации дорожного движения. Использование программных продуктов математического моделирования транспортных потоков при оценке эффективности проектных решений в сфере организации дорожного движения. М.: Минтранс РФ, 2017. 72 с.
4. Цуприков А.А. Пат. 2595027 Российская Федерация, МПК Е21В 44/00 (2006.01). Способ оптимального адаптивного управления процессом бурения скважин / опубл. 20.08.2016. Бюл. № 23.
5. Совершенствование технологии и оптимизация режимов бурения. М.: МНП, ВНИИОЭНГ, сер. Бурение, 1970. 172 с.
6. Цуприков А.А. Анализ математических моделей механической скорости проходки для оптимизации процесса бурения нефтегазовых скважин [Электронный ресурс] // Краснодар: Научный журнал КубГАУ, 2015. № 3(107). URL: http://ej.kubagro.ru/2015/03/pdf/61.pdf.

Автор – сотрудник ФГБОУ «Кубанский государственный технологический университет»
E-mail: tsouprikov@mail.ru