О применении для нормировки классифицированной выборки наблюдений при распознавании объектов по межчастотному корреляционному признаку

Задача распознавания коррелированных сигналов по дискретным выборкам конечного объёма возникает во многих технических приложениях.

Весьма актуальна, например, задача распознавания типов целей [1] или защита РЛС от дискретных коррелированных мешающих отражений [2]. В работе [2] показано, что для классификации отражённых сигналов обнаруженных объектов по их продольному размеру можно использовать характер флюктуаций отражённых сигналов на разных несущих частотах, оценивая межчастотный коэффициент корреляции (1), где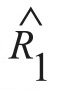– оценка модуля межчастотного коэффициента корреляции,   N – число накоплений по независимым выборкам (обзорам РЛС). Z1_j = x1_j + iy1_j, Z2_j = x2_j + iy2_j – комплексные выборки классифицируемых эхо­сигналов обнаруженного объекта на входе, принятых в двух частотных каналах на разных несущих частотах. В частности, в основе этого сигнального признака классификации лежит взаимосвязь значения межчастотного коэффициента корреляции с линейными размерами объекта. Чем больше размер объекта, тем меньше межчастотный коэффициент корреляции. Однако способ по формуле (1) обладает недостатком, который проявляется в том, что формируемый межчастотный корреляционный признак чувствителен к мощности принимаемых сигналов. Этого недостатка лишён другой способ классификации обнаруженных объектов по их продольному размеру [2], который рассматривается, как способ­прототип, и в котором две выборки наблюдения, принятые на двух разнесённых несущих частотах перемножаются, и их произведение накапливается от обзора к обзору для каждого элемента дальности с обнаруженным объектом, и теперь уже нормированный модуль накопленного произведения 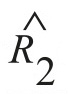сравнивается с порогом (2).

Полученная таким образом оценка модуля межчастотного коэффициента корреляции сравнивается с порогом, на основании чего принимается решение о наличии обнаруженного объекта с большим продольным размером (порог не превышен) или малого продольного размера (порог превышен). Хотя данный способ позволяет осуществлять классификацию объектов по межчастотному корреляционному признаку, однако использование одних и тех же выборок наблюдения как для формирования накопленного произведения, т.е. числитель (2), так и для нормировки к мощности принимаемых сигналов – знаменатель (2), снижает его эффективность. Если же для нормировки оценки модуля межчастотного коэффициента корреляции использовать независимые выборки наблюдений, например, из соседнего элемента дальности, то, как будет показано ниже, это приводит к существенному повышению вероятности правильной классификации объектов.

Таким образом, с целью повышения эффективности распознавания обнаруженных объектов по их продольному размеру предлагается способ классификации, который включает в себя формирование оценки модуля межчастотного коэффициента корреляции с нормировкой на основе двух выборок наблюдений, принятых за несколько обзоров на двух несущих частотах РЛС, и сравнение этой оценки с порогом в элементе дальности с обнаруженным объектом и присвоением при непревышении этого порога в анализируемом элементе дальности признака объекта с большим продольным размером [3].

При этом выборки наблюдений из вспомогательного элемента дальности, принятые за несколько обзоров на двух несущих частотах РЛС, соответствуют предшествующему соседнему элементу дальности по отношению к анализируемому и сохраняются на время, равное длительности элемента дальности.

Таким образом, предлагаемый способ классифицированной нормировки раскрывает новые функциональные возможности распознавания по межчастотному корреляционному признаку. Это позволяет сделать вывод о соответствии заявляемого способа критерию «существенные отличия».

Для того чтобы сформировать межчастотный коэффициент корреляции, в известном способе­прототипе используют операции в соответствии с формулой (2). Важно подчеркнуть, что нормировка производится на основе той же выборки наблюдений, которая используется для расчёта числителя. Решение о том, что объект протяжённый, принимается, если: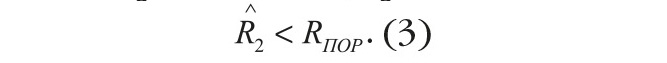Проиллюстрируем работу предлагаемого способа прототипа на конкретном примере, прибегнув как к аналитическому расчёту, так и к моделированию с помощью системы MATLAB [5].

Осуществим классификацию протяжённого объекта, используя две выборки наблюдений с межчастотным коэффициентом корреляции R = 0. Корреляционный порог R_пор в расчётах будем менять от 0,1 до 0,9. Число независимых накоплений (обзоров) возьмём N = 4, 8 и 16.

Для нахождения вероятности правильной классификации протяжённого объекта по непревышению оценкой порога R_пор можно воспользоваться распределением Уишарта. В работе [4] получено распределение оценки модуля межчастотного коэффициента корреляции из распределения Уишарта (4), где Г(…) – гамма­функция.

Для протяжённых объектов R = 0, и распределение (3) можно представить в более простом виде (5).

Используя (5), можно получить формулу для вероятности правильной классификации протяжённых объектов, как вероятность непревышения порога (6).

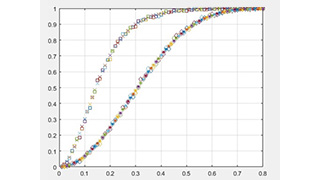
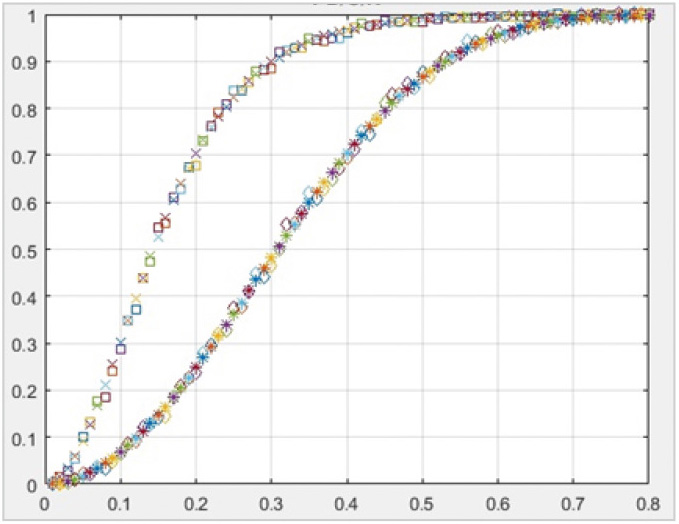
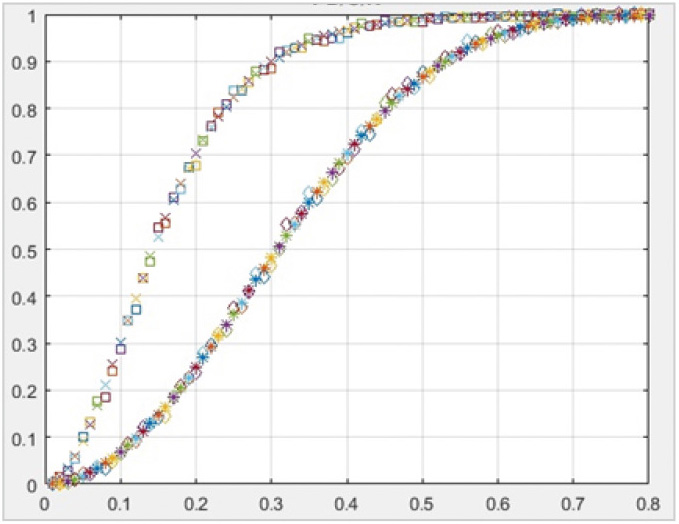
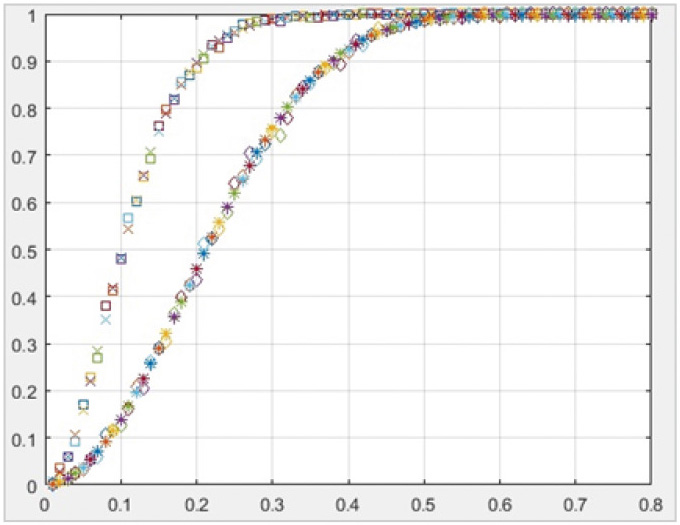
Для верификации данной формулы было проведено моделирование с помощью системы MATLAB [6] классификатора прототипа с расчётом для разных значений порога R_пори числа обзоров N = 4, 8 и 16 (см. рис. 1, 2 и 3, соответственно, где приведена зависимость вероятности правильной классификации протяжённых объектов от порога для оценки модуля межчастотного коэффициента корреляции с нормировкой, как это делается в прототипе, звёздочки – аналитика, ромбики – моделирование (крестики – аналитика, квадраты – моделирование)). Результаты моделирования хорошо совпадают с аналитическими расчётами, что позволяет сделать вывод о достоверности применяемых формул при анализе эффективности способа, используемого в прототипе.

Перейдём к анализу эффективности предложенного способа распознавания. Принципиальное отличие предложенного способа от известного состоит в том, что в формуле (2) для того, чтобы алгоритм был нечувствителен к изменению мощности принимаемых сигналов, нормировку, т.е. деление на знаменатель – оценку мощности сигналов, принятых в двух частотных каналах, производят на основе другой выборки наблюдений, а не той, которая используется для расчёта выражения в числителе (2). Именно поэтому в этом случае нормировка производится независимой выборкой наблюдений. Для этого предлагается производить дополнительные оценки мощности принимаемых сигналов в соседнем элементе дальности на двух несущих частотах: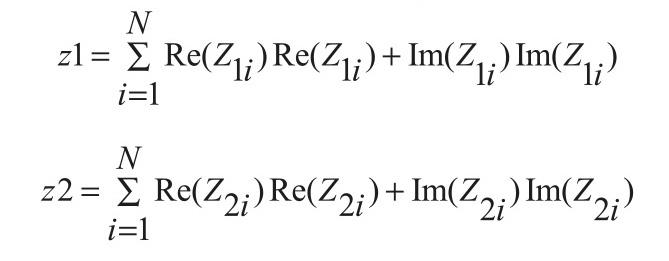Суммирование оценок мощности Z = (z1 + z2) и умножение на R_пор даёт величину адаптивного порога, непревышение которого и есть вероятность правильной классификации протяжённого объекта: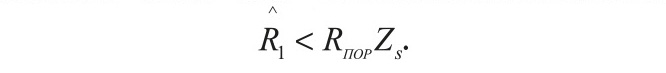Считая независимыми оценки модуля межчастотного коэффициента корреляции, т.е. числителя в (2), и оценки мощности принимаемых сигналов в соседнем элементе дальности, можно получить выражение для вероятности правильной классификации предложенного способа (7).

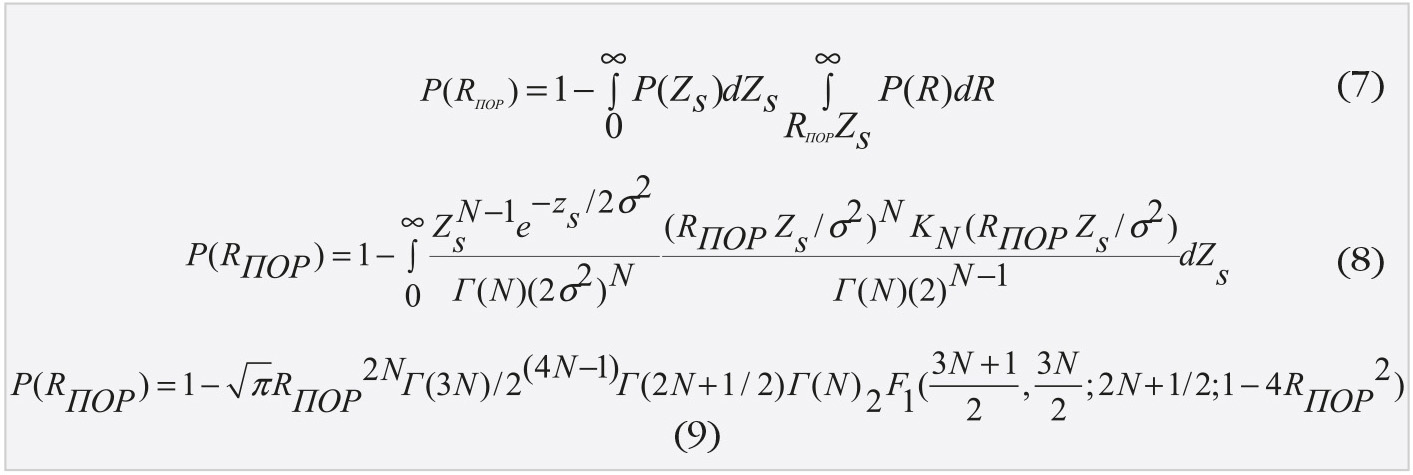
Считая, что оценка мощности принимаемых сигналов Z_s имеет распределение χ², а выражение в числителе (2) имеет распределение [5]: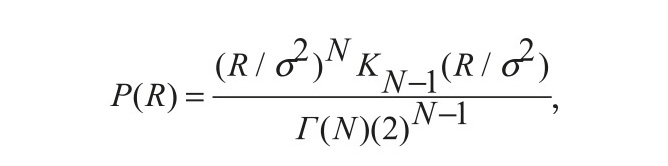где Г(.) – гамма­функция, K_N–1(.) – модифицированная функция Бесселя порядка N–1 и δ² – суммарная мощность принимаемых сигналов, в результате искомая вероятность правильной классификации P(R_пор)примет вид (8).

После взятия интеграла получаем (9), где ₂F₁(.) – гипергеометрическая функция. Дальнейший анализ производился не только аналитическим расчётом по полученной формуле (8), но и, для верификации, моделированием предложенного способа в МАТЛАБ.

Результаты аналитических расчётов и моделирования показали их хорошее совпадение для N = 4, 8 и 16 (см. рис. 1, 2 и 3, соответственно, где приведена зависимость вероятности правильной классификации протяжённых объектов от порога для оценки модуля межчастотного коэффициента корреляции с нормировкой, как это делается в предложенном способе, крестики – аналитика, квадраты – моделирование).

Результаты исследования полностью подтверждают, что применение независимых выборок наблюдения для нормировки оценки модуля межчастотного коэффициента корреляции заметно повышает эффективность классификации. Так, уже за 4 обзора при формировании модуля межчастотного коэффициента корреляции с нормировкой независимыми выборками удаётся получить вероятность правильной классификации протяжённого объекта практически такую же, как при использовании нормировки зависимыми выборками наблюдений за 16 обзоров. 

Литература

Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!