Способ адаптивного корреляционного обнаружения

Введение

Задача обнаружения коррелированных сигналов на фоне некоррелированных случайных процессов по дискретным выборкам конечного объёма возникает во многих технических приложениях. Известен способ корреляционного обнаружения принимаемых сигналов, когда две выборки наблюдения, принятые на двух разных несущих частотах, перемножаются, их произведение накапливается и модуль накопленного произведения сравнивается с фиксированным порогом [1]. Полученная таким образом оценка модуля межчастотного коэффициента корреляции сравнивается с порогом, на основании чего принимается решение о наличии принятых коррелированных сигналов. Данный способ позволяет осуществлять эффективное обнаружение коррелированных сигналов, тем не менее данному способу свойственен недостаток, проявляющийся в отсутствии стабилизации ложных тревог при изменении уровня шума, на фоне которого производится корреляционное обнаружение.

Для стабилизации ложных тревог при корреляционном обнаружении предлагается способ [2], который включает в себя формирование оценки модуля коэффициента корреляции на основе выборок наблюдений, принятых на двух несущих частотах. Также способ включает сравнение оценок с порогом, который с целью стабилизации ложных тревог при изменении уровня шума делают адаптивным, формируемым как произведение коэффициента, определяющего вероятность ложной тревоги, на суммарную оценку мощности шума на двух несущих частотах. Анализ эффективности подобных устройств, особенно для малых выборок наблюдения и низких вероятностей ложных тревог, с помощью статистического моделирования, затруднителен. Нелинейная операция умножения приводит к изменению вида распределений на выходе этих устройств и существенному усложнению анализа с помощью аналитических выкладок.

Если при нахождении характеристик обнаружения точность расчёта вероятности правильного обнаружения допускает моделирование, то для малых вероятностей ложных тревог точность расчёта с помощью статистического моделирования становится недопустимо низкой. По этой причине и была предпринята попытка впервые найти аналитические выражения для расчёта низких вероятностей ложных тревог для нелинейных устройств с умножителем на входе и адаптивным порогом при использовании малых выборок наблюдений.

Вероятность превышения порога огибающей шума на выходе умножителя с когерентным накопителем и фиксированным порогом

Рассмотрим коррелятор с фиксированным порогом и покажем, что при изменении уровня шума изменяется вероятность ложной тревоги на его выходе.

Для расчёта вероятности ложной тревоги для коррелятора с фиксированным порогом воспользуемся следующим выражением (1), где – оценка модуля коэффициента корреляции, N – число накоплений по независимым выборкам.
Z1j = x1_j +iy1_j,Z2_j = x2 + iy2_j –
комплексные выборки сигналов на входе умножителя, разнесённых по частоте в виде аддитивной смеси шума и коррелированного сигнала. Квадратурные компоненты шума имеют нормальное распределение, при этом мощность (дисперсия) равна σ², и среднее распределение, равное 0. Обнаружение сигналов в корреляторе с фиксированным порогом осуществляется путём сравнения полученной оценки модуля коэффициента корреляции с порогом R_ПОР, Rˆ > R_ПОР

Покажем, что изменение мощности шума σ² приводит к изменению вероятности ложной тревоги. Для этого, применяя методику нахождения вероятности ложной тревоги F(R_пор) из [3], получим выражение (2).

В данное выражение входит гамма-функция G(N), модифицированная функция Бесселя K_N(Rˆ_ПОР) порядка N и мощность шума σ².

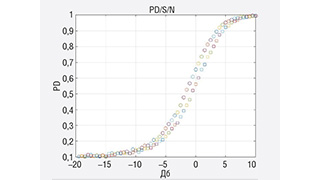
Расчёты по формуле (2) для N=8, приведённые на рис. 1, показывают, что даже незначительные изменения мощности шума на входе (от 0 до 3 дБ) приводят к заметному росту вероятности ложной тревоги. Для верификации аналитических расчётов на графике имеются результаты и моделирования коррелятора с фиксированным порогом в MATLAB. Совпадение аналитики и моделирования подтверждает отсутствие стабильной вероятности ложной тревоги в корреляторе с фиксированным порогом. Ромбики (моделирование) и кружочки (аналитика) на графиках рисунка 1 соответствуют мощности шума 0 дБ, квадратики (моделирование) и звёздочки (аналитика) – мощности шума 3 дБ.

Вероятность ложной тревоги на выходе умножителя с когерентным накопителем и адаптивным порогом

Чтобы устранить указанный недостаток, предлагается производить дополнительно оценку мощности шума на двух несущих частотах, т.е. z1 и z2 (см. (3) и (4)).

Суммирование оценок мощности Z_s=(z1+z2) и умножение на коэффициент, определяющий вероятность ложной тревоги a, позволяет сделать порог адаптивным.

Считая независимыми оценки модуля коэффициента корреляции и оценки мощности шума, можно получить выражение для вероятности ложной тревоги предложенного адаптивного коррелятора, см. (5).

Считая, что оценка мощности Z_s имеет распределение χ², вероятность ложной тревоги F(α) примет вид (6).

После взятия интеграла получаем (7), где ₂F₁: гипергеометрическая функция. Полученное выражение (7) говорит о главном – в нём отсутствует мощность шума σ². В таблице указаны пороги для корреляторов с фиксированным (два левых столбца) и (два правых столбца) адаптивным порогами при разных ложных тревогах и разных N.

Характеристики обнаружения сравниваемых способов корреляционного обнаружения

Дальнейший анализ производился не только аналитическим расчётом по полученной формуле, но и для верификации моделированием корреляционного обнаружения с адаптивным порогом в MATLAB.

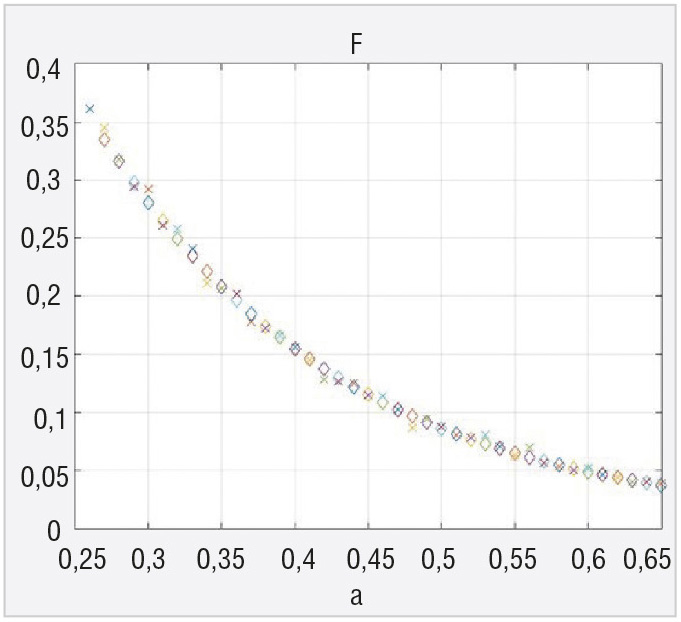
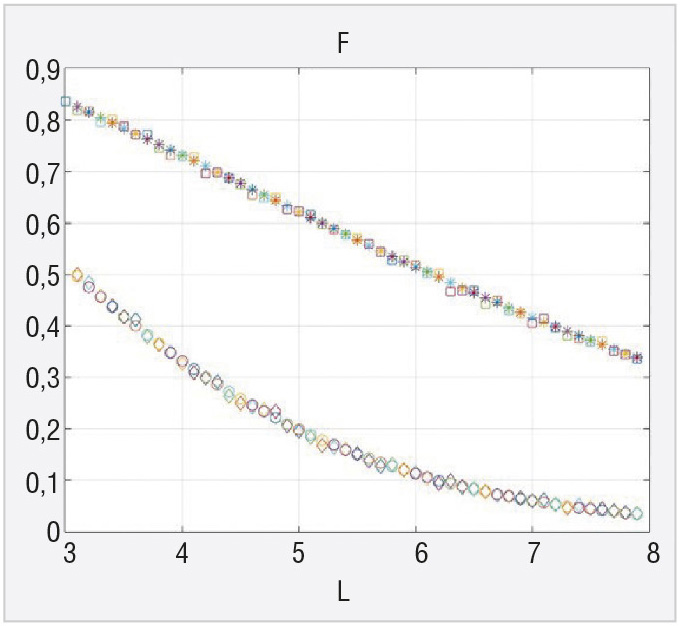
Результаты аналитических расчётов и моделирования показали хорошее совпадение (см. рис. 2), что позволяет сделать вывод о корректности полученного аналитического выражения (7). Ромбики на графиках рисунка 2 соответствуют аналитике, крестики – моделированию. Главный результат, изменение уровня шума в корреляторе с адаптивным порогом, не влияет на вероятность ложной тревоги.

Коррелятор с адаптивным порогом по эффективности сравнивался с коррелятором с фиксированным порогом расчётом характеристик обнаружения флюктуирующего коррелированного сигнала. Это было сделано с помощью моделирования в системе MATLAB. На рисунках 3–8 приводятся кривые для вероятности правильного обнаружения флюктуирующего сигнала с коэффициентом корреляции 0,9 для двух рассматриваемых устройств при N=4, N=8 и N=16 для вероятности ложной тревоги 0,1 и вероятности ложной тревоги 0,0001. Кружочки на графиках рисунков 3–8 соответствуют коррелятору с фиксированным порогом, квадратики – коррелятору с адаптивным порогом.

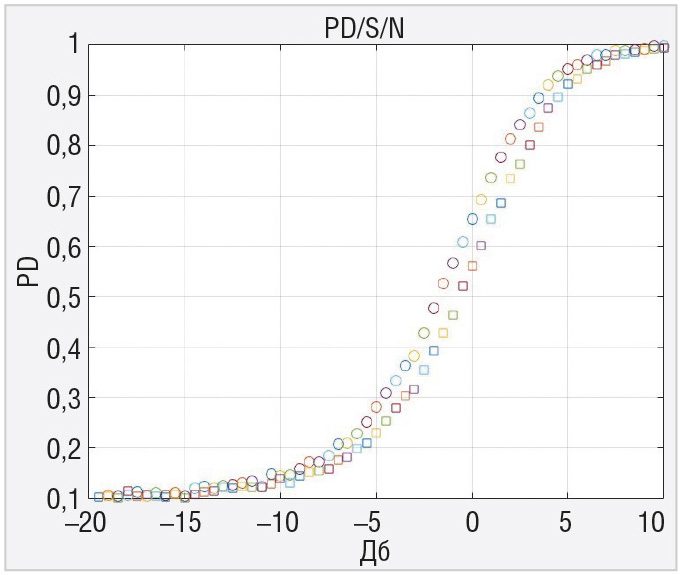
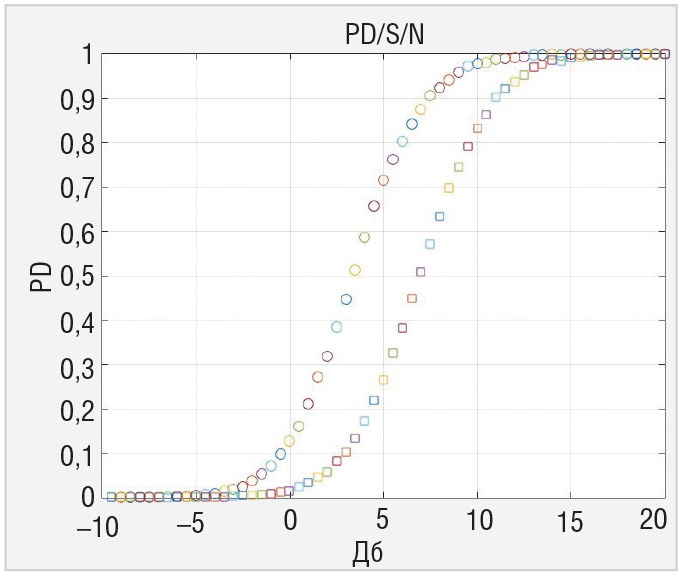
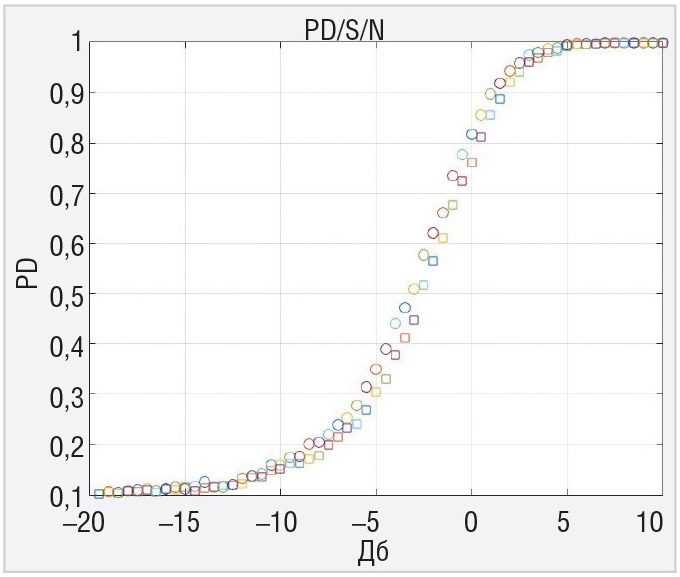
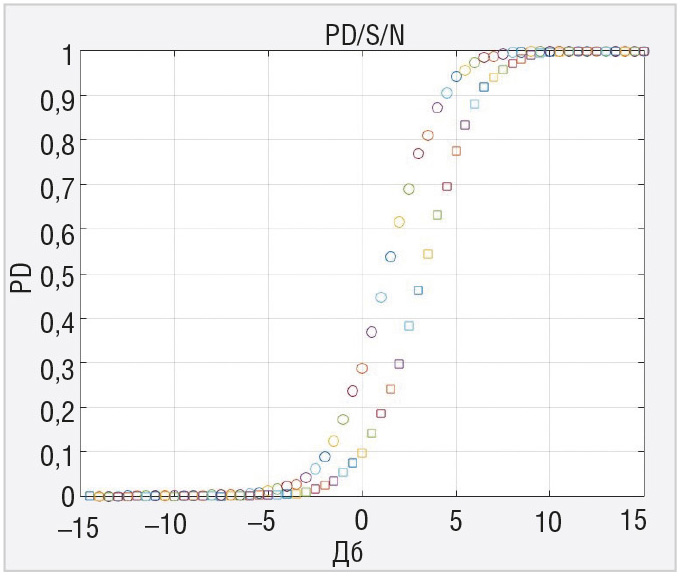
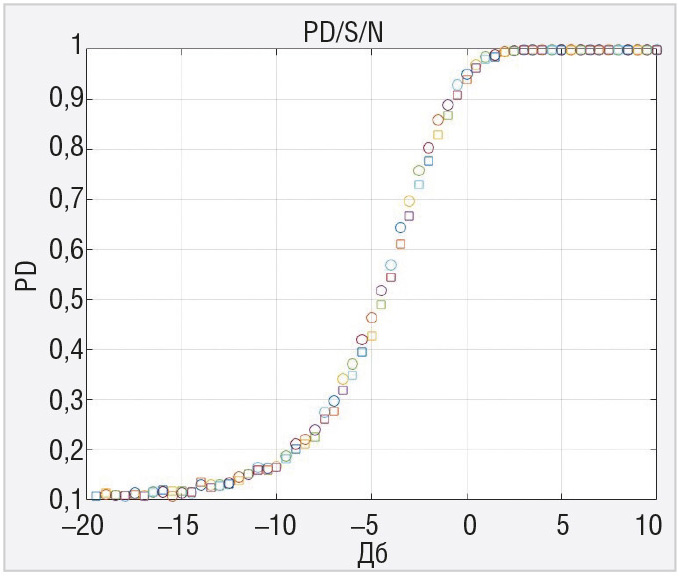
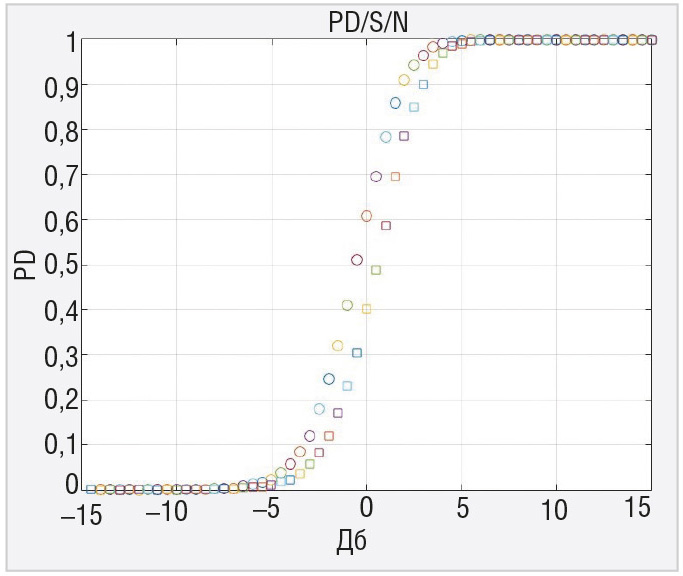
Показано, что эффективность в пороговом сигнале для вероятности правильного обнаружения 0,5 и вероятности ложной тревоги 0,1 и 0,0001 несколько выше у коррелятора без стабилизации ложных тревог, особенно для меньшей вероятности ложной тревоги. Это своего рода плата за инвариантные свойства адаптивного коррелятора к изменениям мощности шума, при этом обеспечивается стабилизация вероятности ложной тревоги на выходе. Следует заметить, что эти потери снижаются при увеличении выборки наблюдений.

Таким образом, проведённое исследование в системе MATLAB полностью подтверждает положительный эффект от применения предложенного коррелятора со стабилизацией ложных тревог. Важно подчеркнуть, что полученное впервые аналитическое выражение для вероятности ложной тревоги адаптивного коррелятора позволит более обстоятельно исследовать его свойства для разных малых выборок наблюдения в широком диапазоне вероятностей ложных тревог.

Литература

Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!