Расчёт собственного импеданса ферритовых втулок в составе электрических цепей на основе измерений во временной области. Часть 1

Введение

Современный этап развития радио­электроники характеризуется существенным усложнением электромагнитной обстановки. Это определяется увеличением пространственной плотности размещения технических средств (ТС), а также смещением частот помехоэмиссии в область больших значений [1], в которых ТС, как правило, обладают меньшей помехоустойчивостью. В этой связи для обеспечения электромагнитной совместимости (ЭМС) на практике применяется широкий арсенал конструкторских и схемотехнических методов, отличающихся по стоимости реализации, эффективности и степени универсальности.

На сегодняшний день одним из самых распространённых способов улучшения показателей ЭМС является использование ферритовых элементов, которые наиболее часто представлены втулками различной конфигурации. Такие втулки размещаются на одиночных и многожильных проводах, шлейфах, а в обоснованных случаях – и на экранирующих и коаксиальных кабелях. Принцип действия ферритовых фильтрующих элементов широко освещён в литературе, например [2], и состоит в создании повышенного полного сопротивления при протекании некомпенсированных токов за счёт взаимодействия формируемого ими магнитного поля с ферритом. Ферритовые втулки (ФВ) предназначены для уменьшения помехонесущих токов синфазного типа, а помехи дифференциального типа ослабляются существенно хуже, что определяется почти полной компенсацией магнитных полей для встречных токов, протекающих в близко расположенных проводниках.

Как и любые другие технические решения, применение ферритовых элементов должно быть обоснованным. Обладая нелинейной зависимостью полного сопротивления от частоты, ферритовые втулки в ряде случаев способны оказывать недопустимо большое влияние на полезные сигналы, в особенности цифровые, вызывая нарушение их информационной целостности. Не менее важным вопросом является сопоставление ФВ разных типов по эффективности ослабления помех в заданной полосе частот, что необходимо для рационального их применения в технических средствах. Ввиду этого важным вопросом практики является оценка собственных свойств ФВ, в первую очередь – зависимостей действительной и мнимой части полного сопротивления от частоты [3]. Как правило, в информационных листах на ФВ отсутствует детальная информация такого рода. В некоторых случаях приводится лишь зависимость полного импеданса от частоты. Однако неизвестность фазовых характеристик не позволяет решать обозначенные выше задачи. Кроме того, зачастую на конкретном образце ФВ отсутствует маркировка, что вовсе делает невозможным определение типа фильтра и получение справочной информации.

Таким образом, вопрос о получении точной информации о собственных свойствах ФВ как элементов электрических цепей остается открытым и настоятельно требующим решения.

Физика работы ферритовых втулок в электрических цепях

Согласно принятой классификации [4], ферриты, применяемые в качестве фильтрующих элементов, относят к высокочастотным материалам с полосой рабочих частот до 1 ГГц. Для создания ФВ с охарактеризованной выше областью применения используются только магнитомягкие ферриты, что обеспечивает малые потери на перемагничивание и сохранение больших значений относительной магнитной проницаемости µ в магнитных полях невысокой напряжённости, характерных для типовых синфазных помехонесущих токов. Ферриты отличаются существенно меньшей индукцией насыщения по сравнению с электротехнической и специализированной сталью, причём достижение насыщения характеризуется падением |µ| до значения порядка единицы. Поэтому в типовом случае ФВ применяются для повышения полного импеданса в цепях со сравнительно небольшим значением некомпенсированного тока. Для ферритов действует ряд ограничений по воздействию повышенной температуры и механических напряжений, которые должны учитываться при выборе условий эксплуатации [5].

Ферриты имеют структуру, во многом схожую с керамикой, и являются диэлектриками, но с пониженным электрическим сопротивлением. В их структуре обычно присутствуют две кристаллические подрешётки, из которых по крайней мере одна обладает антиферромагнитными свойствами. Для изготовления ФВ, как правило, используются никель-цинковые и магний-цинковые ферриты, образованные твёрдыми растворами замещения в структуре шпинели. В ферритах этих типов кристаллическая подрешётка, включающая атомы цинка, не имеет собственного магнитного момента. Меняя концентрацию тех или иных ионов в объёме кристаллической решетки, можно варьировать электрофизические свойства ферритов, что и применяется для получения ФВ с наибольшим полным сопротивлением в той или иной полосе частот.

Сложная кристаллическая структура ферритов определяет электрические свойства ФВ в цепи с некомпенсированными токами. В радиоэлектронных приложениях материалы в основном используются в полосах частот, в которых не наблюдаются недопустимые потери, например на поляризацию диэлектриков. Но применение ФВ в качестве фильтров низких частот составляет исключение. Смена ориентации вектора намагниченности для образца феррита сопровождается энергетическими затратами, которые резко увеличиваются на частотах свыше 1…10 МГц, т.е. в полосе заграждения, и проявляются в виде увеличения полного сопротивления цепи с ФВ.

В настоящее время для моделирования цепей с ФВ широко применяется учитывающее этот факт представление о комплексной магнитной проницаемости [6]. Рассмотрим систему, состоящую из проводника, проходящего через ФВ. Если не учитывать омические потери в проводнике, то для сигнала с некоторой частотой f импеданс составит Z = j2πµfL₀, где j=√–1, L₀ — некоторый постоянный положительный коэффициент, соответствующий индуктивности участка проводника в отсутствие ферритовой втулки; µ — относительная магнитная проницаемость. Потери на перемагничивание учитываются в значении µ, которая приобретает комплексный характер, т.е. µ = µ' – jµ''. Тогда Z = j2πµfL₀ ′ fL₀ + 2πµ ″ fL₀ = jX(f) + R(f), (1) причём в функциях X(f) и R(f) должна быть учтена и зависимость µ′ и µ″ от частоты, которая, как будет показано ниже, может иметь весьма сложный характер. Приведённая формула позволяет обосновать некоторые простые правила выбора конфигурации ФВ. Напряжённость магнитного поля вблизи достаточно протяжённого проводника с током I на удалении r от него составляет H = I/(2pr). Учитывая это, если требуется достичь большего значения Z, то целесообразно использовать плотно прилегающие к проводу длинные втулки небольшой толщины.

Если действительная и мнимая составляющие импеданса известны для некоторой полосы частот, то это позволяет выполнить моделирование ФВ в составе какой-либо схемы или как отдельного помехоподавляющего элемента. Схема замещения ФВ будет состоять из частотно-зависимых индуктивности и активного сопротивления. Столь простое представление весьма сложной физики взаимодействия ферритов с внешними магнитными полями позволяет использовать сравнительно простой способ определения функций X(f) и R(f) для заданной полосы частот.

Определение функций X(f) и R(f) для заданной полосы частот на основе измерений во временной области

Характерные зависимости X(f) и R(f), как это будет показано ниже, могут оказаться весьма сложными. Вместе с тем при выборе способа их экспериментального определения необходимо ориентироваться на доступную измерительную базу. Наиболее распространенные способы измерений параметров сигналов базируются на использовании анализа во временной области, т.е. осциллографии. Как правило, ферриты применяются для фильтрации помех в полосе частот до 1 ГГц, что более чем достижимо для современных средств измерений, например осциллографов компании Rohde & Schwarz серий RTO [7] и RTP [8]. В данном случае запас по рабочей полосе значительно повышает качество результатов измерений. Альтернативный предлагаемому ниже подход может быть построен на применении векторных анализаторов цепей, которые, однако, имеют существенно более высокую стоимость, меньшее распространение и избыточность по характеристикам, чрезмерную для рассматриваемой задачи.

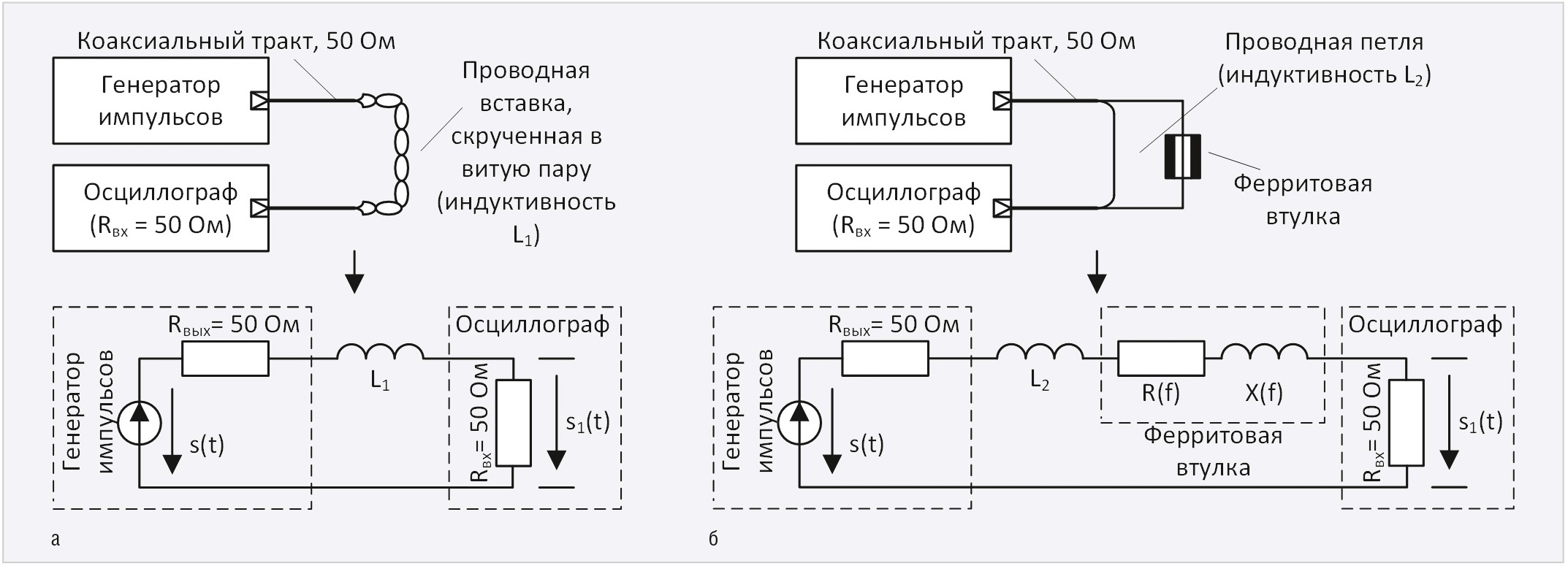
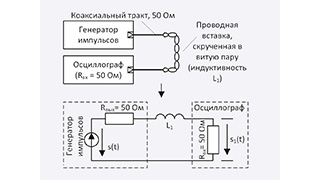
Предлагаемый метод определения функций X(f) и R(f) включает в себя измерительный и расчётный этапы. Для реализации первого из них используют две схемы (см. рис.1), включающие в себя коаксиальный тракт с волновым сопротивлением 50 Ом с проводной вставкой небольшой длины и согласованной нагрузкой, которой может являться и входное сопротивление канала осциллографа. В схеме на рисунке 1а провода вставки скручены в витую пару, которая обычно имеет волновое сопротивление порядка 90…150 Ом [9], т.е. в большей степени проявляет индуктивные свойства. Она может быть смоделирована индуктивностью L₁. Для схемы на рисунке 1б форма импульса будет иной за счёт появления в схеме комплексного импеданса, определяемого свойствами ФВ, а также наличия иной индуктивности L₂, обусловленной расправлением скрученной проводной врезки в контур. Типовой оценочный расчёт значений L₁ и L₂ описан в экспериментальной части работы. Для имитации условий типового применения возвратный проводник должен быть удалён от ФВ на возможно большее расстояние r, такое, чтобы было выполнено условие D²/r² << 1, где D — внешний диаметр ФВ.

С учётом изложенного измерительный этап сводится к регистрации функций сигналов s₁(t) и s₂(t) при неизменных настройках генератора импульсов и в отсутствие заметного влияния измерительной оснастки и трактов осциллографа на результаты измерений, в чём и состоит основное предъявляемое к ним требование. Вопрос выбора формы импульсов, их длительности и периода повторения будет рассмотрен ниже.

Современные средства измерений позволяют документировать форму сигналов не только в графическом виде, но и в виде массива данных, что является предпочтительным, т.к. упрощает выполнение расчётного этапа. При этом совмещение моментов начала или других характерных точек импульсных сигналов s₁(t) и s₂(t) может выполняться, например, в точке t = 0. При этом в пределах временного интервала регистрации импульсы должны укладываться полностью. В случае значительного смещения упомянутых точек на расчётном этапе должна выполняться его компенсация, которая может быть реализована как во временной области, так и в частотной области введением фазового множителя exp(–j2πfΔt) для спектральной плотности сигналов s₁(t) или s₂(t), где Δt — необходимое смещение по времени. В дальнейших выкладках предполагается, что Δt = 0. На практике значение Δt может быть определено совмещением характерных точек импульсных сигналов s₁(t) и s₂(t).

На рисунке 1 показаны соответствующие эквивалентные схемы, из которых, собственно, и следует принцип дальнейшего определения функций X(f) и R(f) на расчётном этапе. Функциям s(t), s₁(t) и s₂(t) можно сопоставить спектральные плотности:

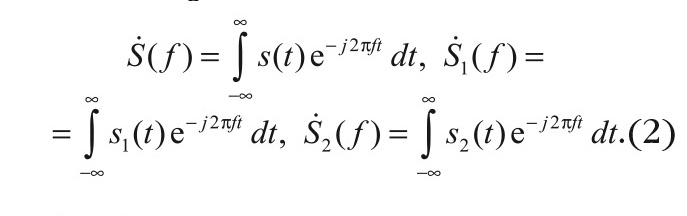
С учётом структуры схемы на рисунке 1а:

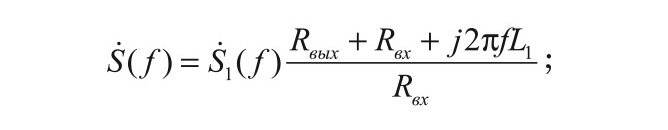
причём в типовом случае R_вых = R_вх = 50 Ом. Схема на рисунке 1б является делителем напряжения с комплексной передаточной функцией вида:

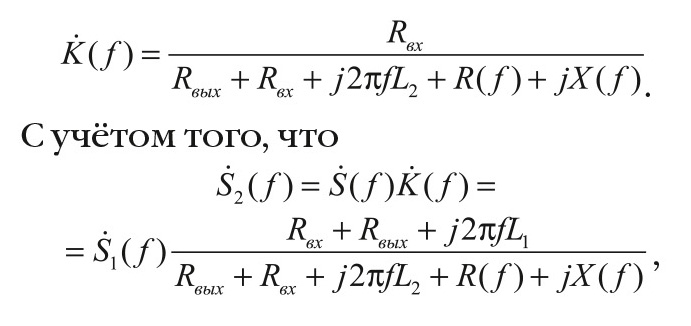
получаем следующее уравнение, определяющее значения X(f) и R(f):

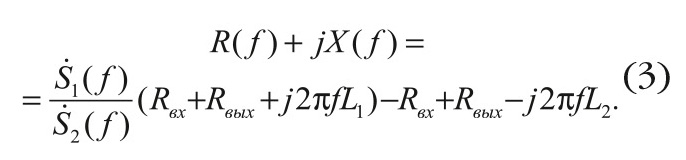
Определение функций X(f) и R(f) всегда выполняется в интервале частот от 0 до f_M, который далее будем называть интервалом идентификации, апеллируя к последующему моделированию ФВ в этой же полосе как основному применению полученных результатов.

Для проверки результатов расчётов можно воспользоваться следующим приёмом. Сигналы s₁(t) и s₂(t) в схемах на рисунке 1 должны измеряться с достаточным запасом по полосе за счёт характеристик осциллографа и измерительной оснастки. На основе обратного преобразования Фурье

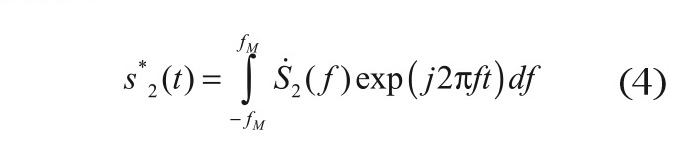
может быть рассчитан сигнал s*₂(t), имеющий спектр, строго ограниченный частотой f_M. В то же время по сходному принципу может быть найден сигнал s**₂(t), также имеющий ограниченную полосу:

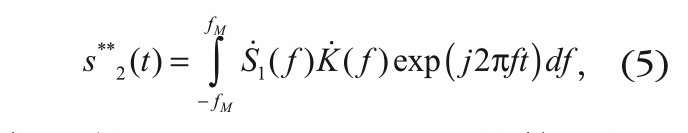
где в расчёте K( f ) используются найденные зависимости X( f ) и R( f ). Сопоставляя вид функций s*₂(t) и s**₂(t), например, с использованием метода наименьших квадратов, осуществляют проверку выполненных расчётов и правильности реализации метода в целом.

Важно подчеркнуть, что магнитные свойства ферритов проявляют зависимости от ряда факторов, в первую очередь от температуры [5, 6]. Поэтому зависимости X( f ) и R( f ), определённые предложенным методом, будут справедливы только в некотором интервале функции вблизи значения, которое было при измерениях. Введение температурных зависимостей свойств ФВ в их модели нерационально, т.к. требует большого объёма исследований и усложняет процесс моделирования, тем самым нивелируя ценность его использования для решения практических задач.

Использование изложенного метода, весьма простого в содержательной части, требует решения двух дополнительных вопросов. Первый из них состоит в выборе оптимальной формы импульса для определения свойств ФВ. Второй относится к области последующего использования результатов построения математической модели ФВ и состоит в аппроксимации формы частотных зависимостей составляющих магнитной проницаемости µ′ и µ″. Решение обоих вопросов предложено ниже. 

Выбор формы и характеристик импульса для определения свойств ФВ путем измерений во временной области

Для достаточно точного расчёта действительной и мнимой составляющих импеданса ФВ необходимо, чтобы комплексный спектр имел значения |S( f )| в диапазоне частот от –f_M до f_M. Наилучшим вариантом являются сигналы с постоянной спектральной плотностью в полосе идентификации, однако их формирование требует использования специальных генераторов и потому затруднено.

Для сравнения рассмотрим одиночные импульсы прямоугольной, косинусоидальной и синусоидальной форм, соответственно описываемые уравнениями:

в которых τ – длительность импульса;

А – амплитудный коэффициент. Каждый из импульсов имеет размах А. Графики функций s_p(t), s_с(t) и s_s(t), построенные для τ = 1 нс и A = 1 В, представлены на рисунке 2.

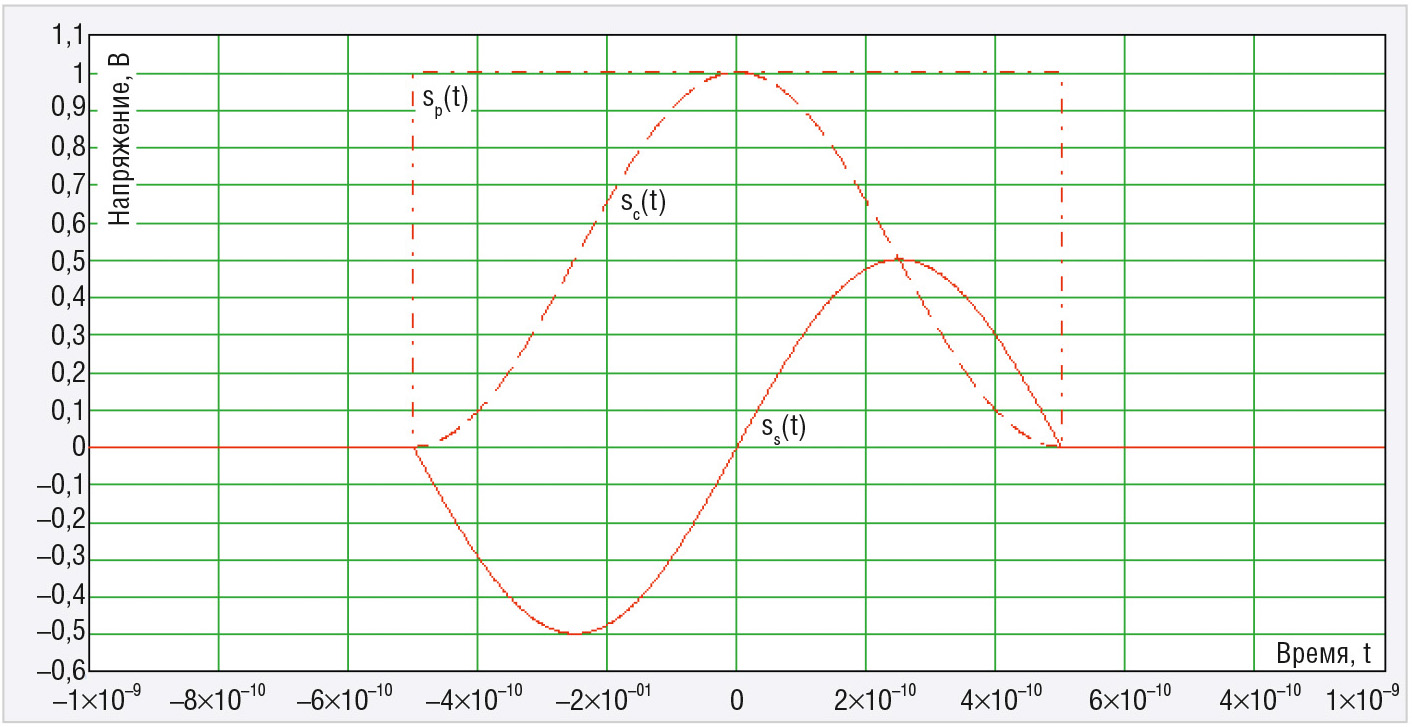
Можно показать, что спектральные плотности функций s_p(t), s_с(t) и s_s(t) имеют следующий вид:

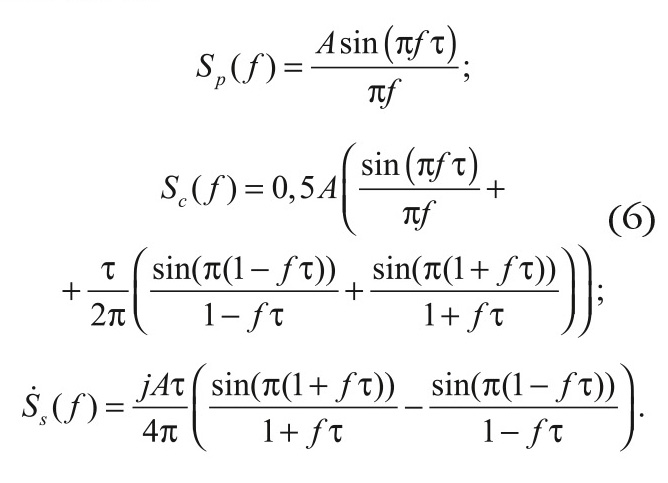
Спектральные плотности функций s_p(t), s_с(t) имеют нулевую мнимую часть, в то время как функция S( f ) имеет нулевую действительную часть. Графики функций S_p( f ), S_c( f ) и jS_s( f ) представлены на рисунке 3 в интервале частот от -4/τ до 4/τ. Первый лепесток спектра для функций s_p(t) укладывается в интервал частот от нуля до 1/τ, в то время как для двух остальных функций первый лепесток занимает полосу до 2/τ.

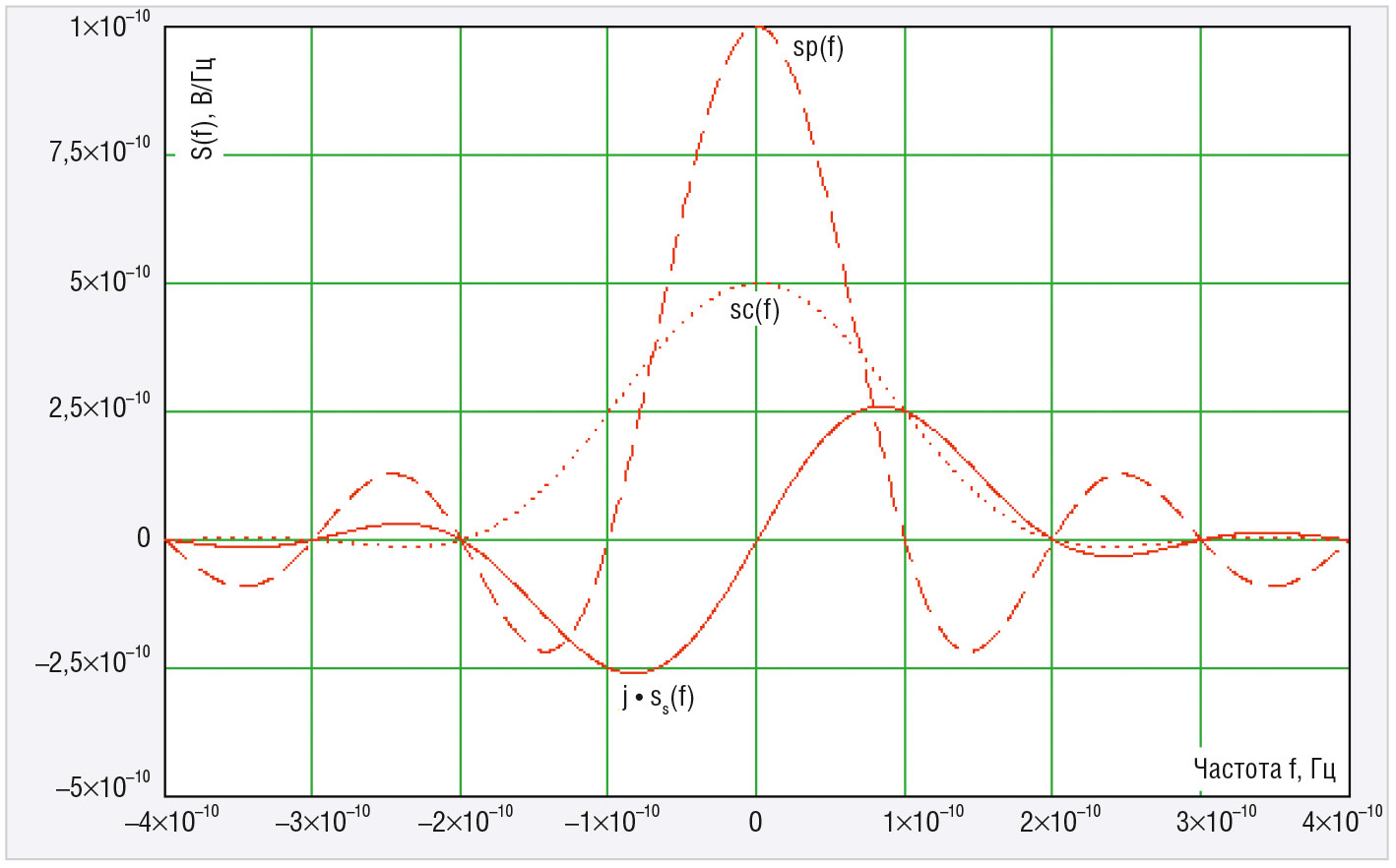
Чем выше значение |S( f )| для конкретного значения частоты, тем больше будут проявляться эффекты, связанные с собственными магнитными свойствами ФВ при её включении в цепь, и тем меньшей «маскировке» они будут подвергаться со стороны нежелательных явлений в измерительной схеме. Известно [10], что в первом лепестке спектра импульсных сигналов обычно сосредоточено до 90% энергии, а спектральные составляющие второго и последующих лепестков значительно меньше по уровню. Ввиду этого целесообразно выбирать длительность импульса вне зависимости от его формы таким образом, чтобы первый ноль его спектра приходился на частоту выше f_M.

Анализируя графики, представленные на рисунке 3, можно видеть, что условие |S( f )| выполняется для всех трёх функций. Функции S_p(f) и S_c(f) характеризуются тем, что имеют наибольшие значения вблизи нулевых частот. С учётом того, что в уравнения X( f ) = 2πμ'fL₀; R( f ) = 2πμ''fL₀ частота входит как линейный множитель, такое распределение спектральной плотности оказывается наиболее рациональным для случаев, когда определение функций X( f ) и R( f ) требуется провести, начиная с близких к нулю частот. При прочих равных условиях использование косинусоидального импульса предпочтительнее, т.к. использование прямого и обратного преобразований Фурье для прямоугольного импульса может сопровождаться появлением эффекта Гиббса при интегрировании в ограниченном интервале частот [11], что осложняет проверку результатов расчётов с применением формул (4) и (5) при использовании встроенных функций математических пакетов. Одиночный импульс синусоидальной формы оказывается более подходящим для измерений характеристик ФВ на частотах диапазона от 0,4/τ до 1,5/τ.

Безусловно, могут быть предложены к использованию импульсы и других форм, например идеальный узкополосный сигнал [10]. Получаемые с их использованием результаты измерений при прочих равных условиях будут в общем случае обладать разной точностью. В наиболее простом случае следует использовать прямоугольные импульсы со значением τ = 0,5/f_M для исключения существенных погрешностей, возникающих при малых значениях спектральной плотности сигнала s₁(t) в схеме на рисунке 1.

Важным вопросом является выбор амплитуды используемого импульса. Интервал возможных её значений ограничен чувствительностью осциллографа и насыщением феррита. Известно [5], что для магнитомягких ферритов индукция насыщения лежит в интервале от 0,1 до 0,5 Тл. Поскольку при типовом применении радиопомехи не обладают уровнем, достаточным для перевода феррита в насыщение, то амплитуду импульса следует выбирать так, чтобы индукция в феррите со значительным запасом не приближалась к нижней границе указанного диапазона. Можно показать, что при |µ| ≈ 5000 насыщение наступает при амплитуде тока в проводнике порядка 6 А, а на практике оно должно быть не менее чем на порядок меньше. При использовании импульсов с А = 1 В и схем измерений, представленных на рисунке 1, формирующий магнитное поле ток не превысит 10 мА, если считать влияние индуктивностей L₁ и L₂ пренебрежимо малым.

Предельное значение импеданса ФВ можно оценить на уровне 1 кОм, при этом амплитуда напряжения на входе осциллографа составит не менее 20 мВ при разумных размерах проводной вставки в скрученном и развёрнутом виде. Этого достаточно для регистрации и измерений формы импульсов при использовании развёртки с ценой деления 10…20 мВ/дел. Таким образом, амплитуда порядка 1 В гарантирует отсутствие насыщения в материале ФВ и соответствует чувствительности современных средств измерений. 

Аппроксимация частотных зависимостей µ' и µ''

Зависимости X(f) и R(f) описывают свойства ФВ как компонентов электрической цепи. Если такие зависимости, полученные экспериментально, предполагается использовать для схемотехнического моделирования, то рационально перейти к аппроксимирующим функциям. Значения µ' и µ'' проявляют зависимость от частоты, вид которой можно определить на основе результатов измерений. Из уравнений (1) следует, что µ'( f ) = X( f )/ (2πfL₀); µ''( f ) =
= R( f )/ (2πfL₀). Значение L₀ может быть оценено на основе справочных данных [12]. Для линейного проводника длиной l и весьма малого диаметра d оно составляет:

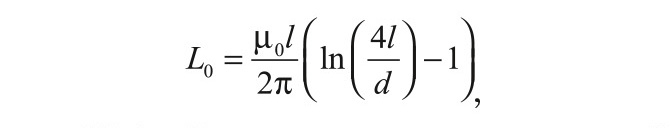
или 32,4 нГн для проводника длиной 3 см и диаметром 0,2 мм. В последней формуле µ₀ = 4π·10^–7 Гн/м — магнитная постоянная. Значение L₀ принципиально может быть рассчитано для ФВ любого типа.

Для выбора вида аппроксимирующих функций целесообразно обратиться к зависимостям µ'( f ) и µ''( f ) для реальных материалов. Их примеры [6] приведены на рисунке 4, для материалов типа 73, 43 и 61 начальные значения магнитной проницаемости составляют соответственно 2500, 850 и 125.

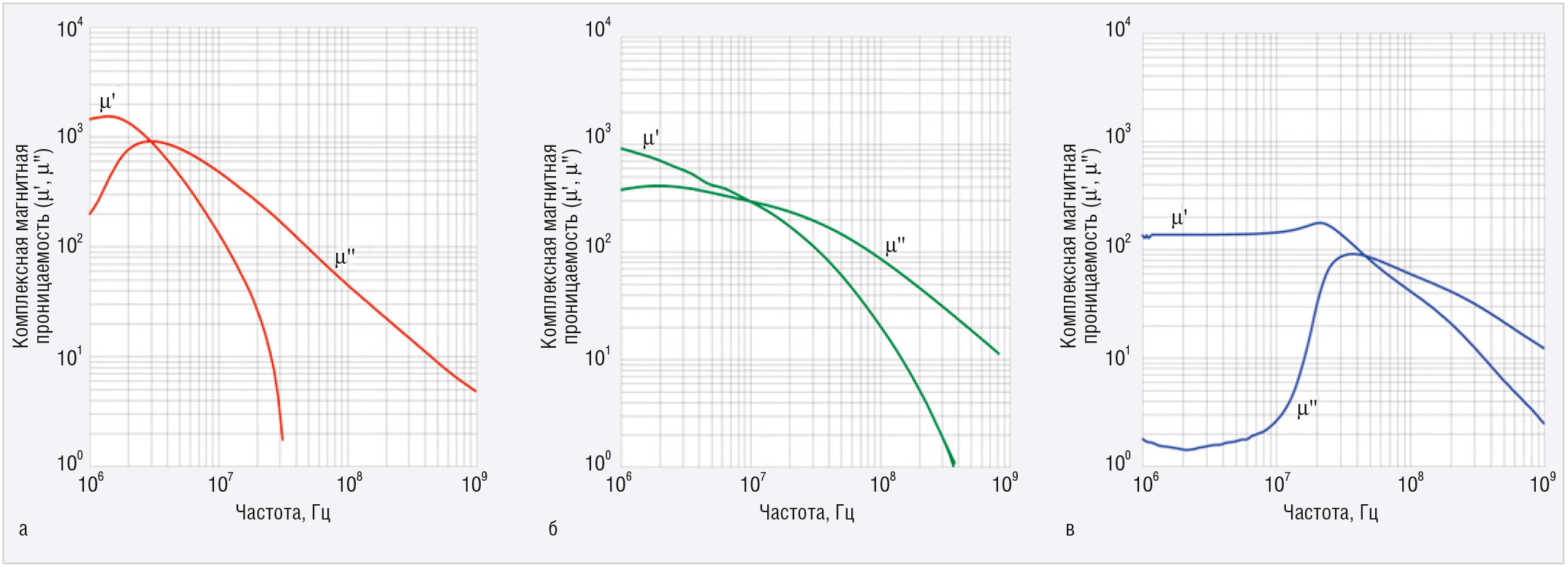
Важно подчеркнуть, что µ' и µ'' имеют ограничения по минимальным значениям. Действительная часть µ определяет индуктивную составляющую импеданса, которая не может быть меньше, чем у проводника в свободном пространстве, поэтому для всех частот min(µ') = 1. Мнимая часть µ для высоких частот может быть менее 1, поэтому min(µ'') ≈ 0, однако на таких частотах существенны такие механизмы потерь, которые в общем случае могут маскировать проявление магнитных свойств ФВ, например значительное повышение омического сопротивления проводников из-за скин-эффекта.

Анализ представленных, а также ряда других аналогичных зависимостей показывает наличие следующих особенностей. Обе кривые имеют выраженные максимумы со значениями M' и M'' на частотах f₀' и f₀'', после экстремума графики в логарифмическом масштабе монотонно убывают по закону, близкому к линейному. До экстремума функции µ'( f ) и µ''( f ) могут иметь немонотонный характер (см. рис. 4в) с характерным спадом в начальной части частотного диапазона. Для аппроксимации этих зависимостей предлагается использовать зависимости одинакового вида:

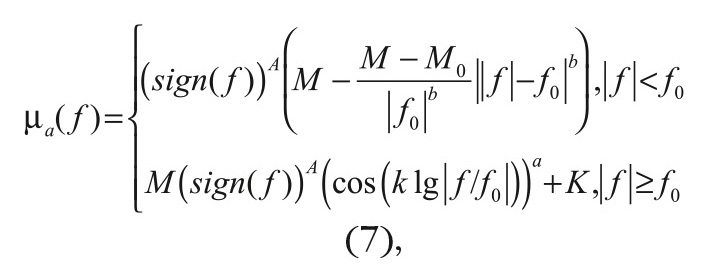
где M₀ — значение компонента магнитной проницаемости вблизи нулевой частоты; sign(a) — функция определения знака аргумента, причем sign(α) = 1, если α ≥ 0, и sign(α) = –1, если α < 0; a, b, k — коэффициенты, причём в типовых случаях a = 1…500, b = 1…10, k = 0,01…0,7; K и A — коэффициенты. При этом K = 1, A = 2 для µ’( f ) и K = 0, A = 1 для µ''( f ). Штриховые обозначения в формуле (7) опущены. Функция µ_a( f ) является чётной при интерполяции кривой µ'( f ) и нечётной во втором случае.

В некоторых случаях средняя погрешность аппроксимации может составлять до 20…40% а в некоторых случаях – и более. В особенности это касается случая немонотонного нарастания µ''( f ) для значений | f | < f₀''. Однако такое значение погрешности следует признать приемлемым, т.к. допуск на импеданс ФВ относительно значения, заявленного для конкретной частоты, обычно составляет ±(20…50)%. В этом состоит основное ограничение использования формул (7). Однако представленные формулы позволяют перейти к приближённым аналитическим выражениям для компонентов магнитной проницаемости, которые удобно использовать в моделировании ФВ.

Для определения коэффициентов аппроксимирующих формул используется непосредственно зависимость µ'( f ) или µ''( f ). По ней определяют значения M, M₀ и f₀, далее способом наименьших квадратов подбирают значения остальных коэффициентов. Предложенный подход был реализован для кривых µ'( f ) или µ''( f ), представленных на рисунке 4а. Графики аппроксимирующих функций и узлы отсчёта невязок в методе наименьших квадратов показаны на рисунке 5. Здесь M' = 1600; M'' = 850; f₀' = 1,5 МГц; f₀'' = 3 МГц. Аппроксимация выполнена при средней погрешности около 35%.

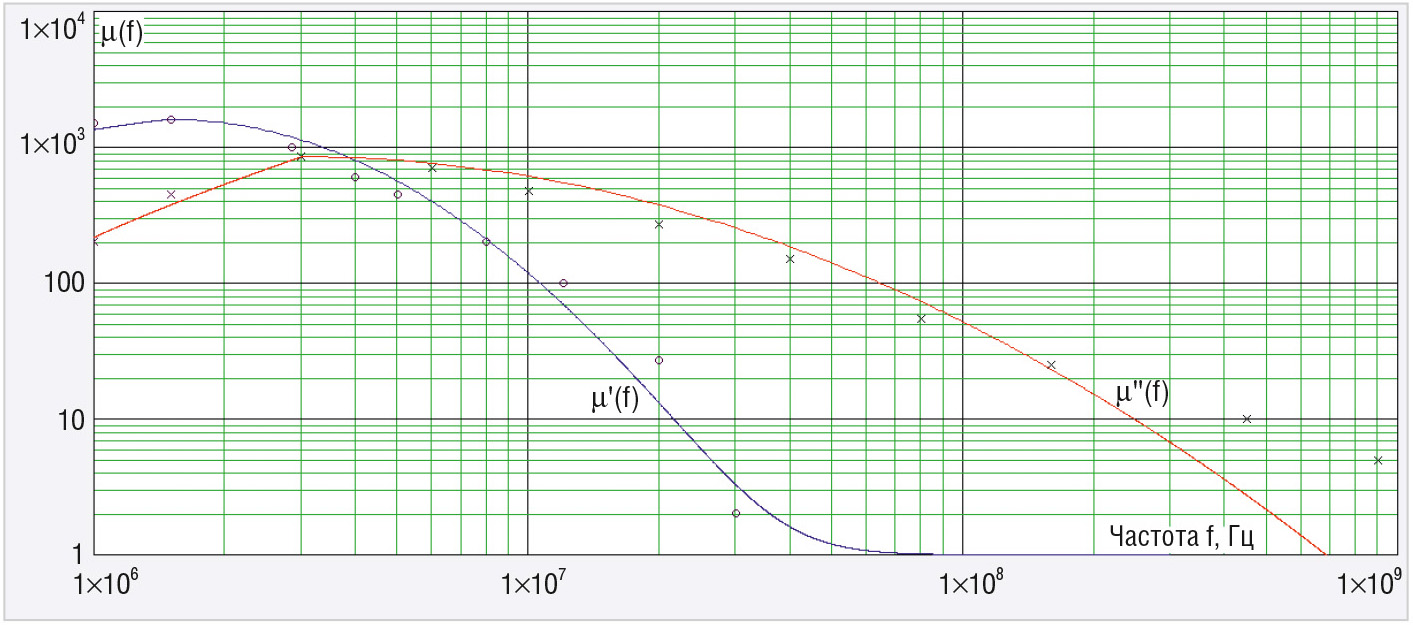
Во второй части статьи будет рассмотрено типовое изменение формы импульсов при наличии ФВ в измерительной схеме и приведены примеры измерений зависимостей X( f ) и R( f ). 

Литература