Существует ряд электронных компонентов, охлаждаемых, главным образом, посредством печатной платы: транзисторы цепей питания, силовые диоды, микросхемы без радиаторов и т.д. Для таких элементов 90% (и более) теплового потока от компонента отводится через плату. Поэтому корректный учёт структуры печатной платы становится важнейшей задачей.
У микросхем, охлаждаемых через установленный на них радиатор (процессоры, память, мосты, ПЛИС), в плату уходит порядка 5–10% от общего теплового потока, и им, как правило, в процессе моделирования пренебрегают. Однако зачастую такую методику расчёта переносят на всю исследуемую систему, что нередко приводит к существенным ошибкам.
В настоящей статье проводится сравнение разных методик теплового моделирования печатных плат и исследуется их влияние на конечный результат анализа – температуру компонентов.
Постановка задачи и методы моделирования
Сложность задачи корректного моделирования печатной платы зависит от устройства самой печатной платы и сложности устройства в целом. Простые печатные платы с малым числом слоёв (1–2) и небольшой площадью (100…200 см2) могут быть без особых трудностей детально промоделированы с использованием классических 3D-решателей без каких-либо упрощений. Однако подавляющее большинство современных электронных изделий строятся на более сложных печатных платах, имеющих более полутора десятков слоёв и площадь в несколько сотен десятков квадратных сантиметров. Детальное моделирование внутренней структуры таких плат классическими 3D-решателями потребует существенных временных затрат и вычислительных ресурсов.
Задача моделирования заключается в построении вычислительной сетки с разрешением, достаточным для расчёта модели с требуемой точностью. Структура же печатной платы такова, что соотношение её длины и ширины к толщине слишком велико для разбиения расчётной модели на конечные объёмные элементы [1]. Толщина слоёв проводника измеряется микронами, а протяжённость трасс проводников – единицами и десятками сантиметров. Сетка для такой структуры содержит десятки и сотни миллионов ячеек, что потребует больших вычислительных ресурсов. Даже с учётом доступности современных вычислительных мощностей, их использование для подобных задач не является оправданным. Поэтому инженеры-расчётчики вынуждены искать компромиссное решение и упрощать структуру платы при моделировании.
Существуют следующие основные методы моделирования печатных плат:
- Детализированное моделирование печатной платы без упрощения её реальной структуры.
- Усреднение свойств теплопроводности при помощи материала с анизотропными свойствами проводимости – отдельно поперечная и продольная проводимость. Продольная проводимость моделирует теплопроводность в медных слоях проводников, поперечная – теплопроводность от слоя к слою, через текстолит и переходные отверстия.
- Усреднение свойств теплопроводности с учётом слоистой структуры платы. Свойства материала задаются в зависимости от количества и толщины слоёв проводников и доли металлизации в каждом слое.
- Усреднение свойств послойно по двумерной сетке. Каждый из слоёв разбивается двухмерной сеткой с заданным разрешением. В пределах каждого квадрата сетки тепловые свойства структуры печатной платы усредняются.
- Комбинированные методы – сочетание разных методов, когда, например, наиболее критичные участки платы вокруг горячих компонентов моделируются с большей детализацией, чем вся плата.
Не все средства САПР для теплового моделирования позволяют реализовать все рассмотренные выше методы. Проблемы, как правило, возникают при использовании детализированной модели и усреднении по сетке. Детализированную модель бывает непросто корректно перенести из ECAD в САПР теплового моделирования, а утилиты усреднения по двумерной сетке, к сожалению, имеются не во всех программных средствах теплового моделирования.
Ниже проводится сравнение двух методов моделирования печатной платы в различных САПР. В САПР № 1 (SolidWorks Flow Simulation) классическим 3D-решателем строится модель с усреднением свойств платы при помощи анизотропного материала. В САПР № 2 (Cadence Sigrity) выполняется детализированное моделирование структуры платы с использованием 2,5D-сетки.
В качестве примера для расчёта используется модель силового диода с участком печатной платы. Силовой диод (выпрямитель с барьером Шоттки) является хорошим примером электронного компонента, охлаждаемого преимущественно через плату, что предусмотрено конструкцией его корпуса – D2PAK или TO263. При этом важно знать, насколько сильно он будет нагреваться, т.к. от температуры существенно зависят электрические характеристики диода. Неверная оценка нагрева диода может привести к недооценке его нагрева и получению неработоспособного устройства или к переоценке и необходимости построения избыточной системы охлаждения, т.е. к увеличению сложности устройства, его массы, габаритов, стоимости и времени разработки.
Существует несколько методов теплового моделирования электронных компонентов, характеризующихся разной точностью, сложностью, применимостью в той или иной расчётной САПР и т.д. Используемые методы моделирования и тепловые модели делятся на два больших класса – детализированные тепловые модели (DTM – Detailed Thermal Model) и компактные тепловые модели (CTM – Compact Thermal Model) [2]. В зависимости от решаемой задачи и доступности, необходимых для расчёта данных, выбирается та или иная модель. В настоящей статье используется двухрезистивная модель компонента – 2R-модель.
Для наглядности при моделировании решается внешняя задача, имитирующая простейший случай – охлаждение платы с установленным компонентом посредством естественной конвекции, без корпуса. Температура окружающей среды задаётся равной +25°С.
Модель и результаты моделирования в САПР № 1
При моделировании в САПР №1 строится упрощённая модель части электронного устройства, т.е. моделируется непосредственно сам диод-выпрямитель и участок платы 100×100 мм, посредством которого осуществляется охлаждение.
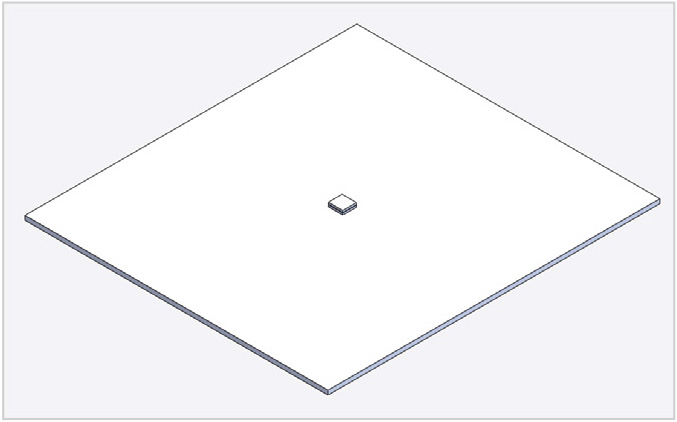
Сам диод-выпрямитель представляется 2R-моделью, геометрия компонента описывается двумя параллелепипедами с размерами, аналогичными размерам корпуса, как показано на рисунке 1.
Данный метод удобен тем, что в документации на электронные компоненты обычно указывают данные по тепловым свойствам как раз для такой модели, а именно: тепловые сопротивления «источник – плата» (RθJB) и «источник – корпус» или «источник – окружающая среда» (RθJC или RθJA). Стоит отдельно упомянуть одну особенность, связанную с указанием сопротивлений для компонентов, охлаждаемых через платы. Фактически, охлаждение таких компонентов идёт через корпус на плату, поэтому сопротивление «источник – корпус» (RθJC) стоит трактовать как сопротивление «источник – плата» и в модели задавать его именно так. Сопротивление «источник – окружающая среда» фактически эквивалентно сопротивлению «источник – корпус» для компонентов, охлаждаемых через радиатор. В расчётных САПР, как правило, для 2R-моделей задаются сопротивления «источник–корпус» и «источник–плата», и незнание указанной выше особенности может привести к путанице и неверным результатам моделирования.
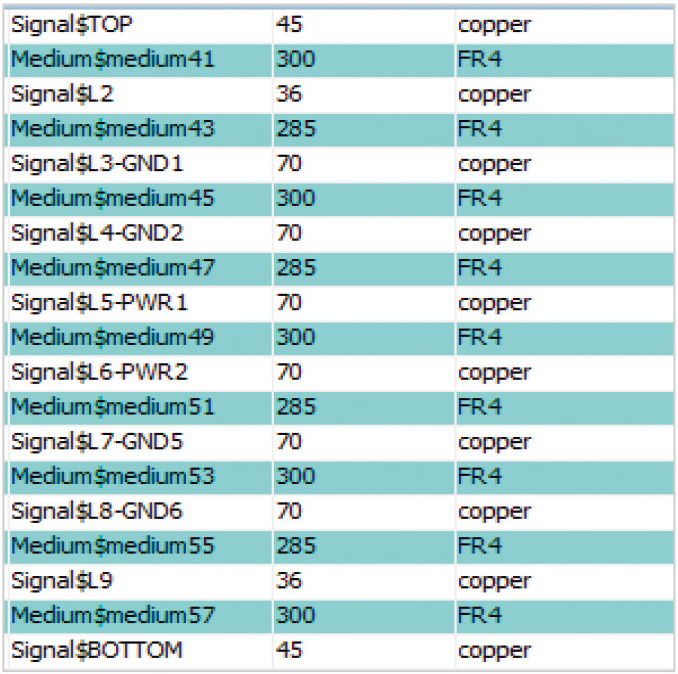
Плата описывается параллелепипедом с соответствующими размерами и анизотропным материалом со свойствами, рассчитанными из усреднения стека слоёв реальной платы, с поперечной теплопроводностью 0,45 Вт/м•К и продольной теплопроводностью 131,5 Вт/м•К. Металлизация по слоям задаётся в 90%. Стек платы показан на рисунке 2.
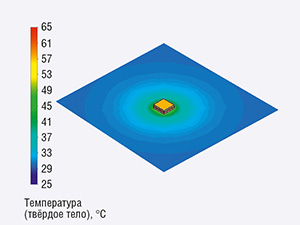
Максимальная температура компонента составила +60°С. Температурное поле на поверхности модели показано на рисунке 3. Далее требуется оценить влияние топологии печатной платы на температуру диода.
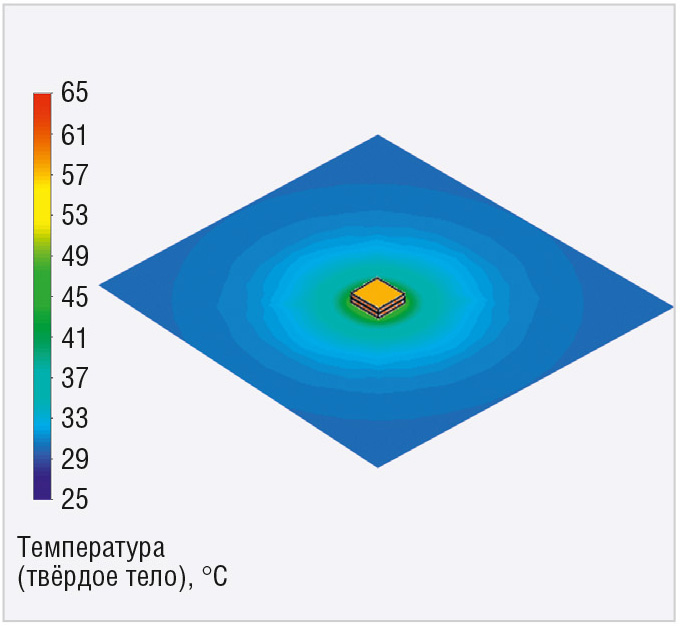
Модель и результаты моделирования в САПР № 2
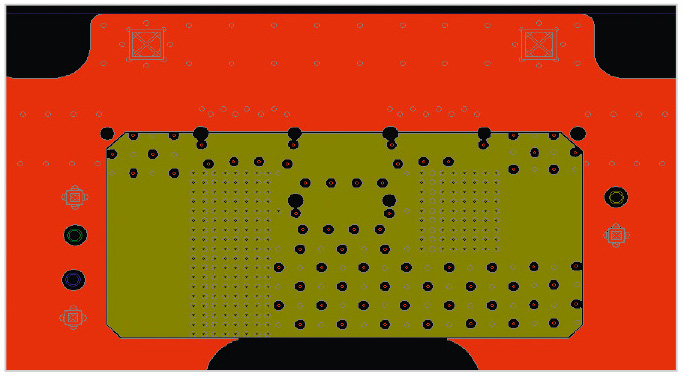
Сравним теперь результаты моделирования в САПР № 1 с результатами моделирования в САПР № 2, где учитывается детализированная структура печатной платы. Модель компонента в САПР № 2 задаётся в виде 2R-модели с соответствующими тепловыми сопротивлениями. Печатная плата моделируется детально, с учётом структуры слоёв (cтек платы показан на рисунке 2), разводки трасс внутри слоёв и переходных отверстий. На рисунке 4 показан верхний слой печатной платы. Как видно из рисунка, электронный модуль обладает тройным дублированием канала питания, и в один момент времени функционирует только один канал.
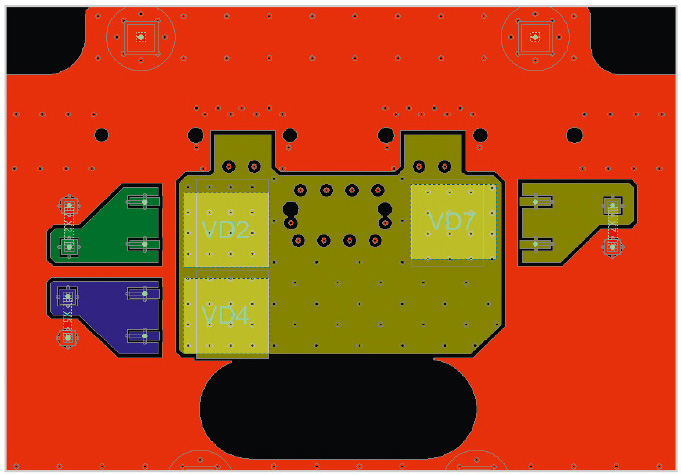
В результате моделирования расчётная температура нагрева диода составляет +80,5°С. Температурное поле показано на рисунке 5. Видно, что результат моделирования в САПР № 2 отличается в большую сторону от результатов моделирования в САПР № 1 приблизительно на 20°С.
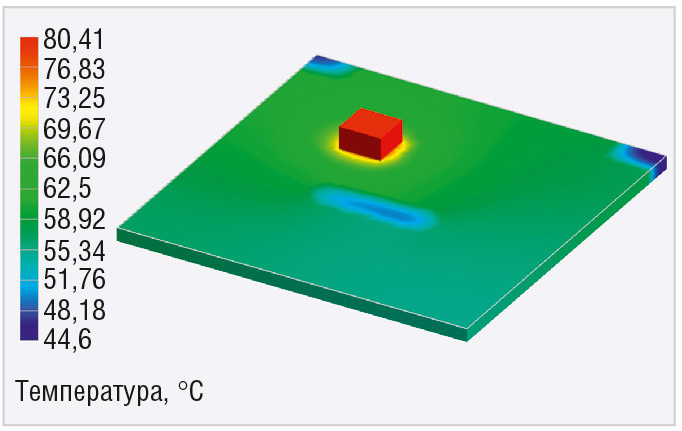
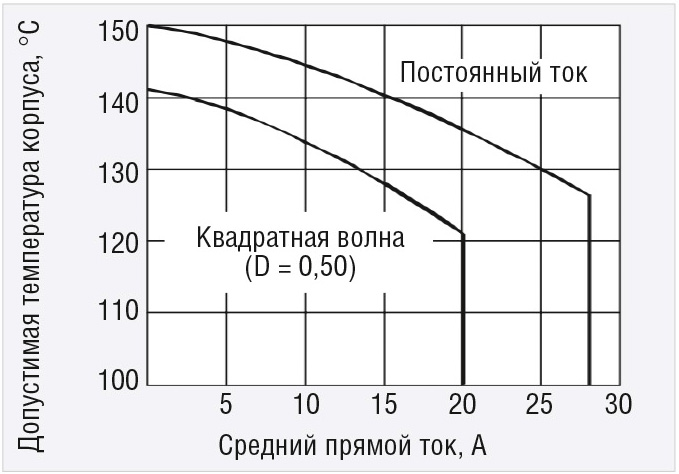
Как видно из графика зависимости среднего прямого тока от температуры (см. рис. 6), падение тока начинается при температуре корпуса около +120…+125°С [3]. Полученная в расчётах температура не является критической для диода в заданных условиях эксплуатации. Однако в реальных изделиях температурный диапазон окружающей среды, как правило, достаточно широк – от –40 до +55°С. При размещении электронного модуля в герметичном корпусе охлаждение диода ещё более ухудшится. В таком случае недооценка нагрева на 20…25°С может привести к приближению реальной температуры к эксплуатационному порогу и спровоцировать перебои в системе питания.
В чём же причина столь большой разницы в расчётах? Обнаружилось, что в модуле токопроводящие слои сформированы не совсем обычно. Полигон питания с верхнего слоя (Top) через переходные отверстия соединяется только с нижним слоем (Bottom) и через разъёмы питания направляется на следующий электронный модуль в стойке. Распределение температуры по переходному отверстию показано на рисунке 7.
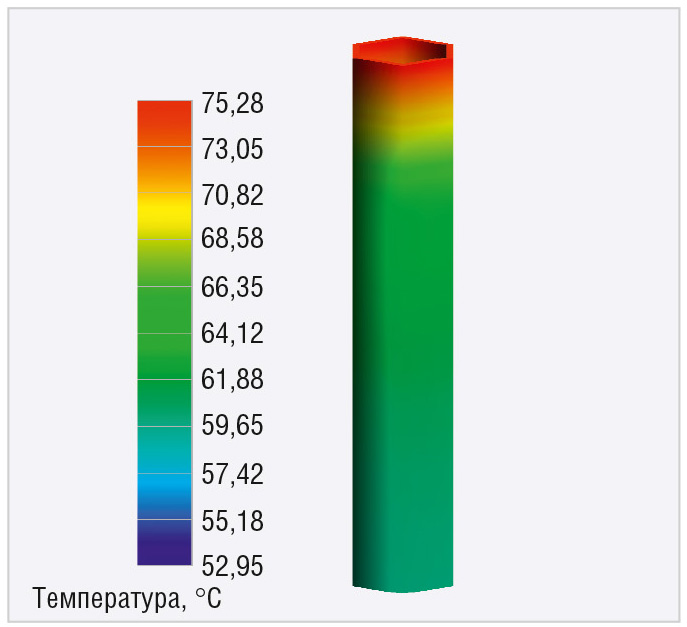
По результатам расчёта температура переходного отверстия в верхнем слое равна +75,5°С, а в нижнем слое – +60°С. Таким образом, разница составляет более 15°С. Следовательно, теплопроводности переходных отверстий недостаточно для качественного распределения теплового потока, и печатная плата препятствует качественному охлаждению диода.

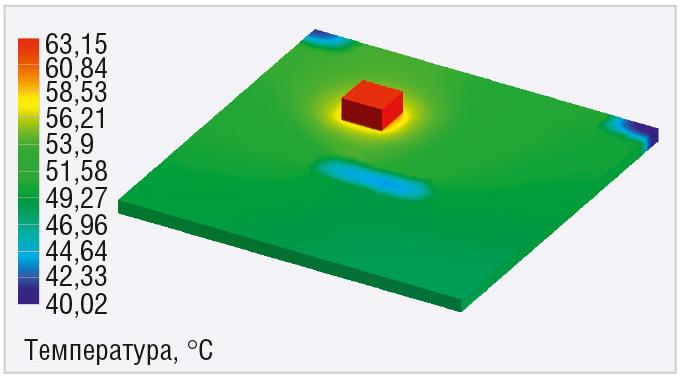
Было принято решение добавить полигоны питания на внутренних слоях и уплотнить шаблон переходных отверстий под площадкой диода. На рисунках 8 и 9 показан один из внутренних слоёв платы до и после оптимизации соответственно. В результате оптимизации расчётная температура диода снизилась до +63°С. Температурное поле показано на рисунке 10.
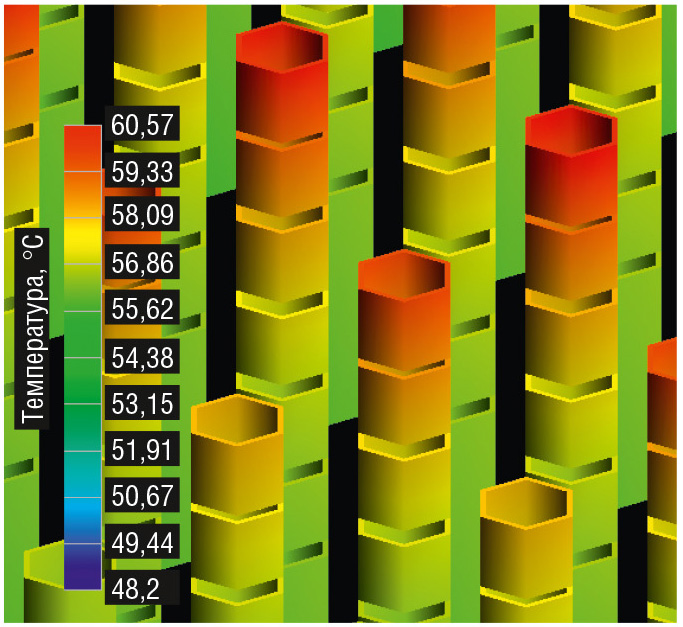
По результатам расчётов температура переходного отверстия в верхнем слое оказалась равной +60°С, а в нижнем – +56°С, разница между ними составила всего 4°С. Распределение температуры по переходному отверстию показано на рисунке 11.
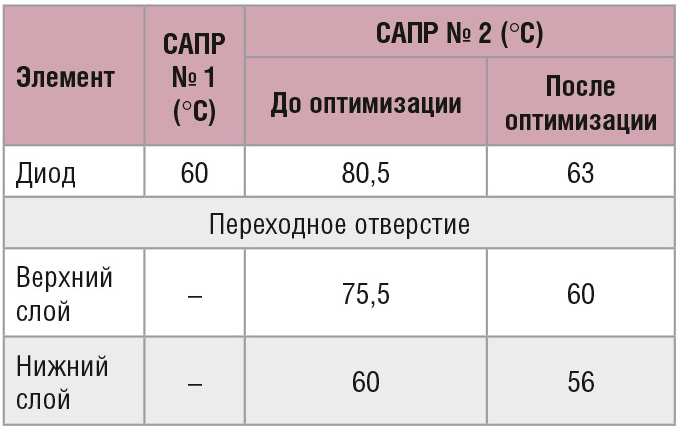
Расчётные температуры представлены в таблице.
Выводы
Учёт реальной топологии печатной платы при моделировании теплового состояния радиоэлектронной аппаратуры позволяет устранить неопределённость, возникающую при использовании анизотропного материала, а также выбирать направление оптимизации более осмысленно.
Дополнительно стоит отметить, что такое моделирование позволяет рассчитать тепловое состояние электронного модуля с учётом разогрева от протекающих токов и оценить влияние температуры на физические характеристики меди. Это, в свою очередь, повлияет на уровень падения напряжений и плотности токов. Данный эффект при моделировании был сознательно отключён, так как САПР № 1 не позволяет его учитывать.
Понимание границ применимости средств моделирования повышает вероятность получения результата, коррелирующего с реальными испытаниями, обеспечивает нахождение оптимального технического решения с минимальными временными затратами и улучшает технико-экономические характеристики изделия.
Литература
- Зенкевич О. Метод конечных элементов в технике. – М.: Мир, 1975.
- Решетников А., Мичурин В. Особенности применения детализированных тепловых моделей для тепловых расчётов микросхем в корпусах BGA, LGA и PGA. Современная электроника. №5, 2019. С. 44–47.
- Vishay Semiconductors, High Performance Schottky Rectifier, 2 x 20 A. URL: https://www.vishay.com/docs/94963/vs-42ctq030shm3.pdf
Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!