Верификация VHDL-описаний цифровых устройств, представленных в виде композиции управляющего и операционного блоков. Часть 2. Верификация на основе функционального покрытия

Введение

В настоящее время возрастание сложности проектируемых систем, реализуемых на программируемых логических схемах типа FPGA и системах на кристалле, на передний план при проектировании выдвигает проблемы верификации, понимаемой как проверка соответствия высокоуровневых VHDL-моделей цифровых систем спецификациям на их разработку. Такая верификация реализуется на основе моделирования и требует создания сложных тестирующих программ, различных по назначению тестов и соответствующего управления тестированием [1]. Одним из направлений такой верификации является функциональная верификация, базирующаяся на генерации псевдослучайных тестовых наборов и функциональном покрытии. Для функциональной верификации VHDL-моделей цифровых систем предложена соответствующая методология, называемая OS-VVM (Open Source VHDL Verification Methodology) [2], некоторые аспекты которой описаны в [3].

Данная статья является продолжением статьи [4], в которой рассмотрена методика верификации VHDL-моделей цифровых устройств с использованием покрытия VHDL-кода, выполняемая в системе Questa Sim [3]. Для цифровых устройств, состоящих из управляющего и операционного блоков, под функциональной верификацией будет пониматься проверка выполнения всех имеющихся в VHDL-модели управляющего блока (автомата) переходов между внутренними состояниями, как синхронных, так и асинхронных. Под функциональной верификацией операционного блока понимается проверка использования при моделировании некоторых либо всех значений каждого из операндов этого блока для каждого из состояний управляющего блока. В статье будет использоваться тот же пример цифрового устройства system, VHDL-описание которого приведено в [4].

Функциональная верификация конечных автоматов на основе покрытия VHDL-кода

Большим достоинством системы моделирования Questa Sim является то, что модель FSM (Finite State Machine) конечного автомата может быть верифицирована, если она написана по определённому шаблону: автомат должен иметь конечное число внутренних состояний, должны быть переменные текущего и следующего состояний, смена которых должна проходить по синхросигналу, при этом следующее состояние должно зависеть от текущего. Именно в таком виде записан конечный автомат fsm, являющийся управляющим блоком цифрового устройства system [4].

Средства (опции моделирования) с покрытием кода позволяют при компиляции VHDL-модели и её моделировании распознать в составе модели устройства конечный автомат fsm, входящий в состав проекта, отследить (учесть) все пройденные (в конкретном сеансе моделирования) состояния конечного автомата и подсчитать число прохождений ориентированных дуг в графе переходов автомата fsm. Чтобы выполнить покрытие VHDL-кода, нужно провести компиляцию модуля fsm с установленными опциями (вызвать окно Compile Properties, в открывшемся окне установить флаг Enable Finite State Machine Coverage и другие флаги для выполнения покрытия VHDL-кода), после чего компиляция выполняется стандартным образом. Перед выполнением моделирования во вкладке Start Simulation → Others нужно установить флаг Enable Code Coverage, выполнить моделирование, например командой Run all, и получить временнýю диаграмму. Тестирующая программа для моделирования устройства system приведена в листинге 1.

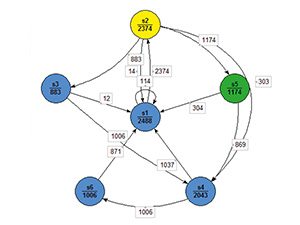
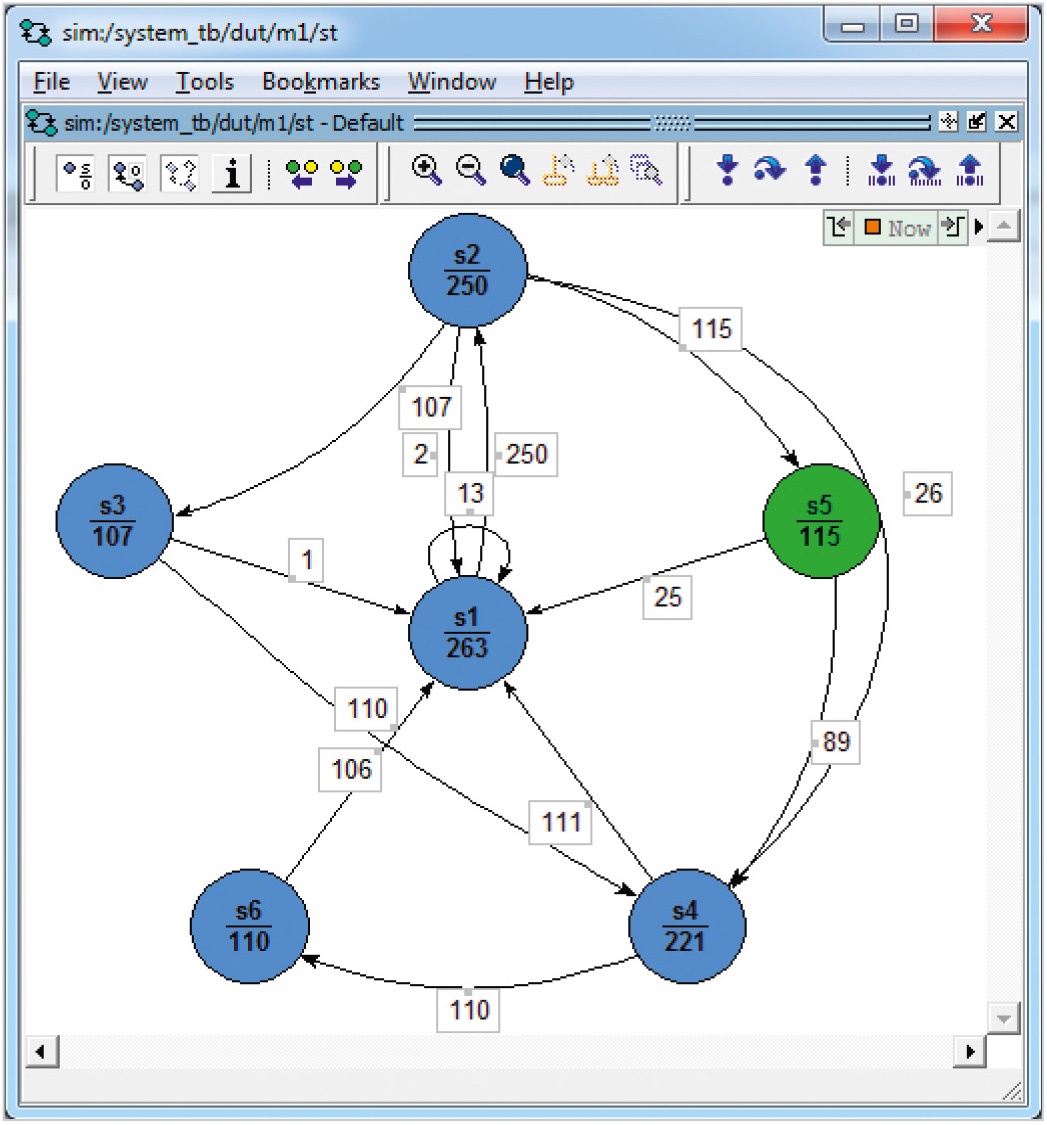
Результаты её выполнения будут анализироваться как для покрытия VHDL-кода управляющего автомата fsm, так и при анализе результатов функционального покрытия устройства system. Просмотр покрытия VHDL-кода автомата в графическом виде может быть выполнен несколькими способами. Первый способ состоит в нажатии левой клавишей мыши на сигнале st, который помечен на временно́й диаграмме (окно Wave) особым образом . Именно внутренний сигнал st (это и есть сигнал, задающий перечислимый тип внутреннего алфавита конечного автомата fsm) ассоциируется с автоматом. Нажав на сигнал st, можно увидеть граф переходов состояний автомата и соответствующую статистику переходов на выполненном тесте (см. рис. 1).

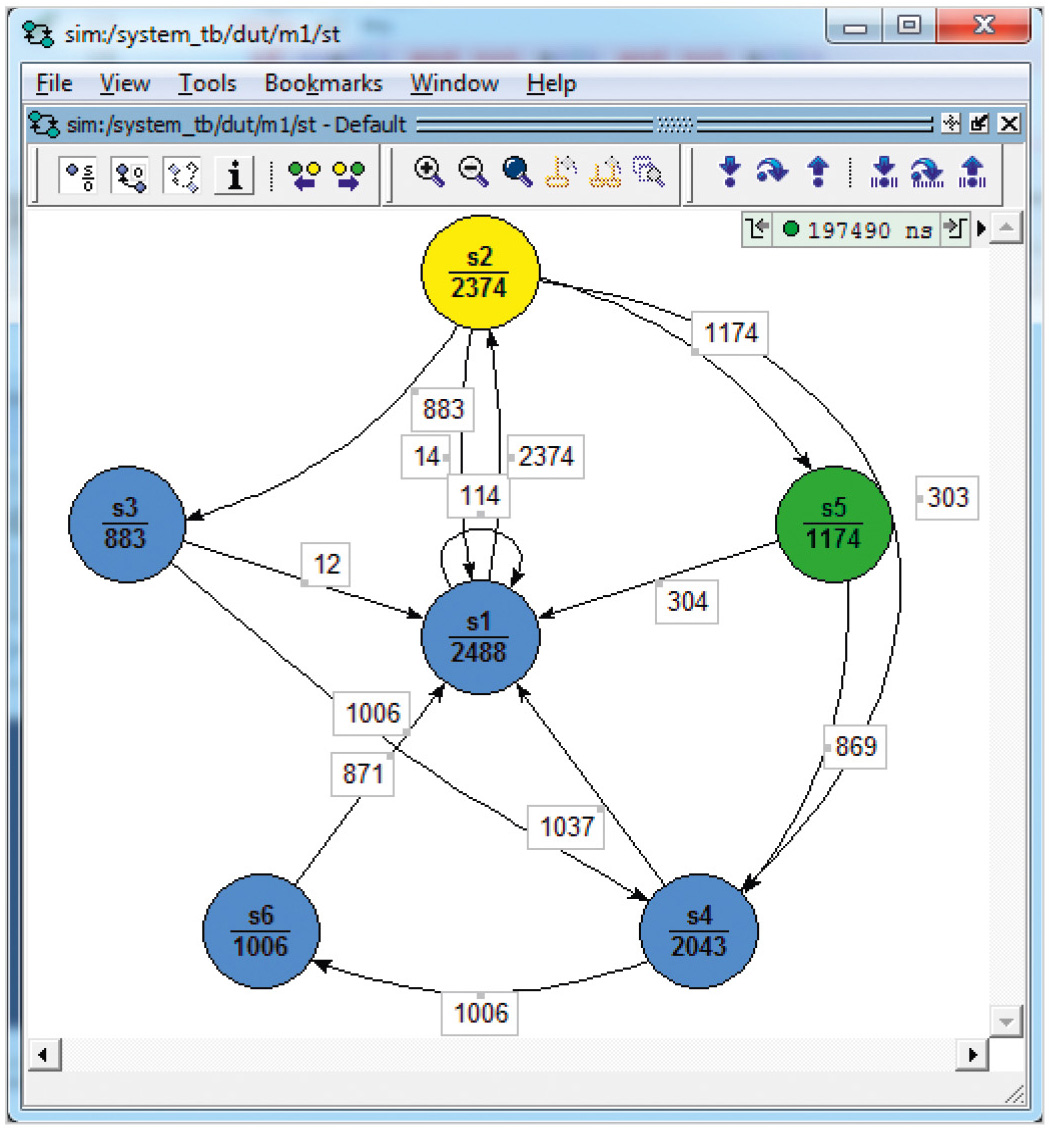
В окне можно переходить из состояния в состояние (вперёд либо назад), нажимая кнопку переднего и заднего фронтов, перед этим установив требуемый отсчёт времени. Например, можно установить нулевое время и провести моделирование согласно тесту, наблюдая в графическом виде за переходами между состояниями. Жёлтым цветом подсвечивается текущее состояние, зелёным – следующее состояние. Не участвующие в данном переходе вершины имеют синий цвет. Красные дуги отмечают непокрытые переходы, цифры на дугах соответствуют числу покрытий (прохождений) этих дуг при моделировании. Эти числа попадают также в текстовые и HTML-отчёты о покрытии автомата. Заметим, что в данном примере все дуги (и состояния) оказались пройденными, причём многократно.

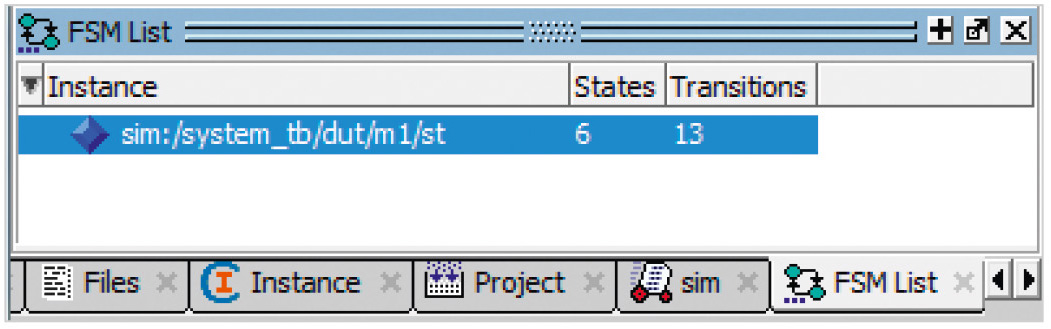
Второй способ визуализации графа состояний автомата – последовательное открытие окон View → FSM List (см. рис. 2). После двойного щелчка левой клавишей мыши на отмеченной строке появится граф автомата.

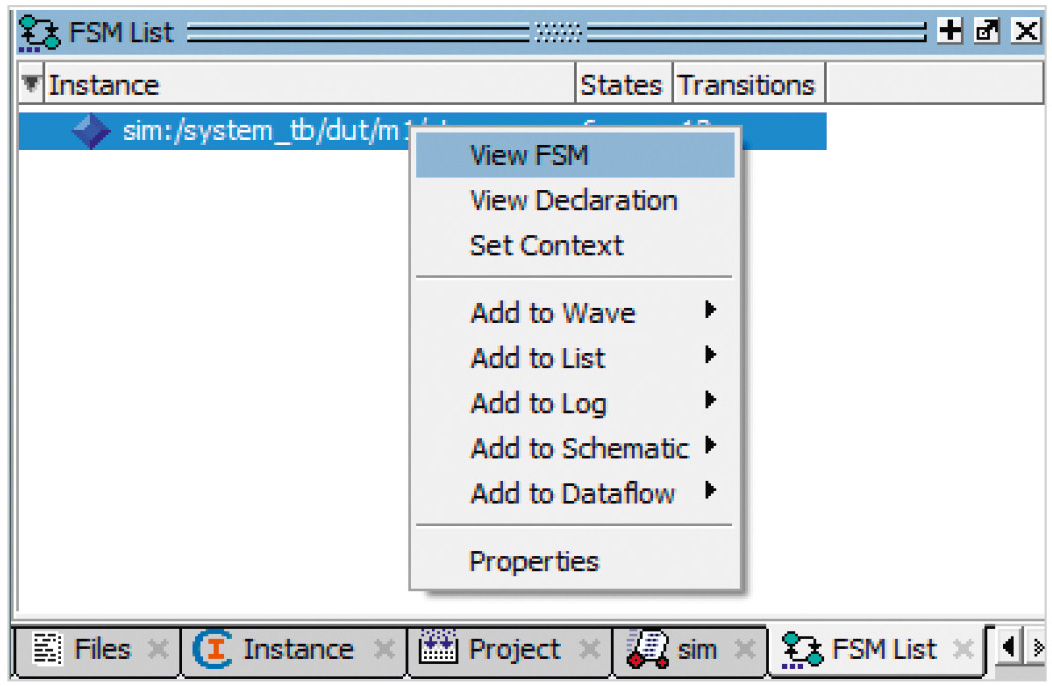
Можно на отмеченной строке (см. рис. 2) нажать правую клавишу мыши, после чего выбрать View FSM (см. рис. 3) – в этом случае также можно увидеть граф автомата (рис. 1).

Из рисунка 1 ясно, что переход s₁ → s₂ был покрыт 2374 раза: этой цифрой помечена соответствующая дуга на графе (см. рис. 1). Результат покрытия автомата на заданном тесте можно сохранить в текстовом виде, как показано в листинге 2. На графе и в текстовом отчёте (см. листинг 2) указываются как синхронные, так и асинхронные переходы между состояниями автомата.

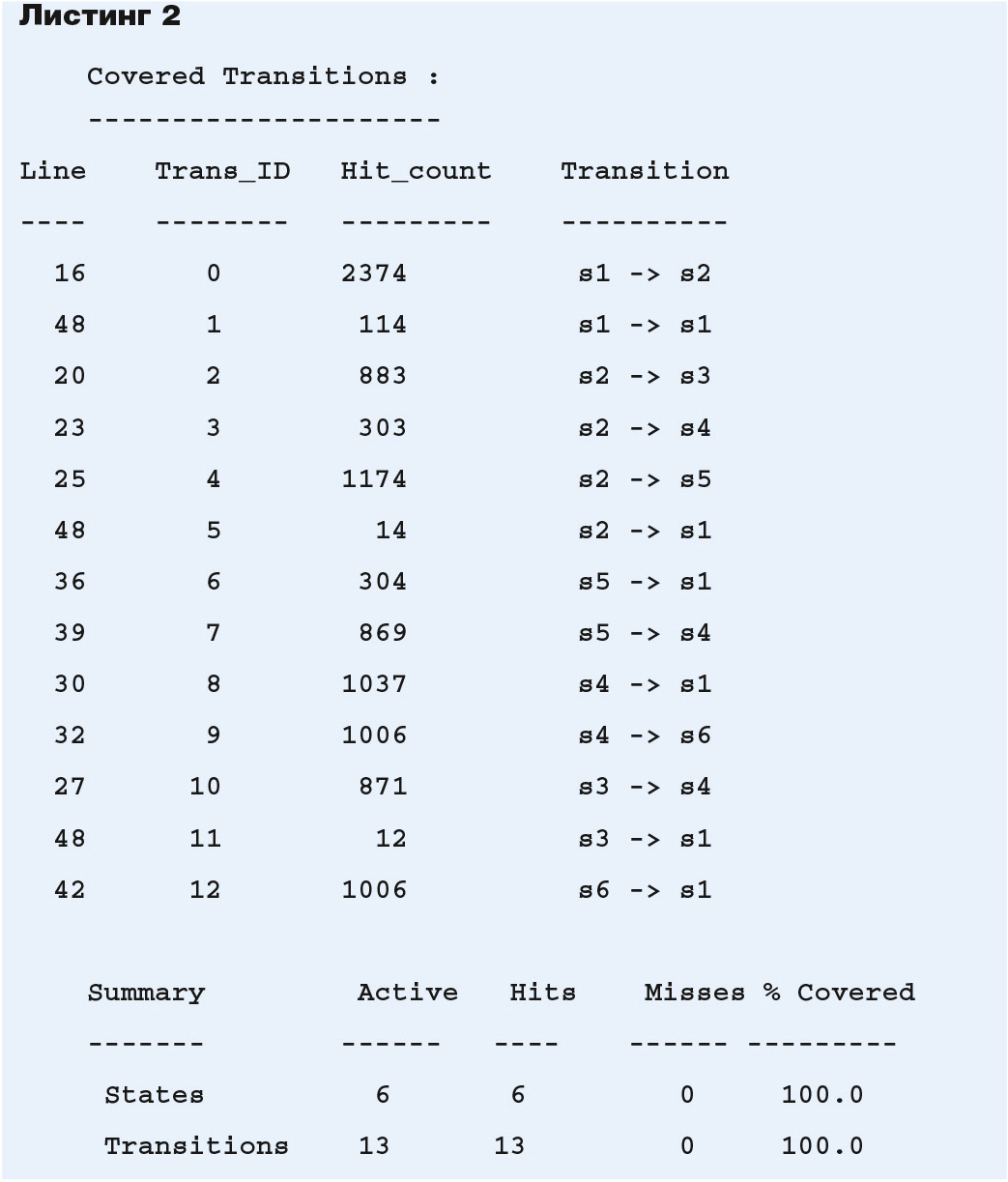
Если требуется по VHDL-модели автомата получить список всех переходов, то в окне Transcript компиляция модели устройства выполняется по команде vcom -fsmverbose t D:/system/fsm.vhd. Если же требуется получить циклы на графе переходов автомата, то необходимо добавить опцию -fsmmultitrans в командную строку вызова компилятора vcom -fsmverbose t -fsmmultitrans D:/system/fsm.vhd.

Получающиеся текстовые отчёты могут быть обработаны программно для составления тестов и проверки выполнения при моделировании всех переходов и требуемых циклов в графах управляющих автоматов.

Верификация на основе функционального покрытия

Тестирующая программа (см. листинг 1) составлена так, чтобы выполнить функциональное покрытие модели устройства, а именно для каждого из шести состояний s₁…s₆ управляющего автомата требуется выполнение соответствующей операции в операционном блоке над парой значений операндов a, b. Каждый из операндов может принимать значения от 0 до 15, в этом случае получается 6×16×16=1536 всех возможных состояний на входах операционного блока. Если же размерности операндов a, b большие, например число разрядов векторов a, b равно 32, то перебор всех возможных состояний операционного блока является трудоёмкой вычислительной процедурой.

Для подтверждения работоспособности операционного блока будет избыточным подавать на вход 1536 тестовых векторов, поэтому предлагается способ сокращения числа входных векторов. Для этого значения каждого из операндов a, b распределим по подмножествам (корзинам). Корзины для каждого из операндов a, b заданы следующим образом: корзина 1 – значение 0; корзина 2 – значения из диапазона 1…4; корзина 3 – значения 5…9; корзина 4 – значения 10…14; корзина 5 – значение 15. Таким образом, число 6×5×5=150 входных тестовых векторов сократится на порядок. Подробное описание корзин, перекрёстных корзин, типов данных и процедур, используемых в тестирующей программе, дано в [4]. В строках 5–7 подключаются VHDL-пакеты RandomPkg, CoveragePkg из библиотеки osvvm, позволяющие использовать методологию верификации OS-VVM. Генерация входных векторов для входных сигналов x, a, b, rst тестируемого устройства выполняется с помощью псевдослучайного генератора – для этого используются четыре переменных (RndX, RndA, RndB, RndRst) типа RandomPType (строки 25–28 в листинге 1). Настройка начального значения псевдослучайного генератора для каждой переменной осуществляется с помощью метода InitSeed (строки 43–46). Генерация псевдослучайных значений сигналов x, a, b осуществляется с помощью метода RandSlv (строки 62–64, 73–75). Для сигнала rst не подходит обычный генератор с равномерным распределением вероятностей выпадения значений, для него необходимо, чтобы значение 1 выпадало значительно реже, чем значение 0. Чтобы задать разную вероятность выпадения значений 0 и 1, используется метод DistValSlv( ((0, 100), (1, 1)), 1) – в этом случае вероятность выпадения 0 равна 100/101, а вероятность выпадения 1 – 1/101 (строки 76–77). Следует отметить, что одноразрядный сигнал rst объявлен как вектор (std_logic_vector(0 downto 0)) единичной длины (строка 21) – это связано с тем, что метод DistValSlv (как и метод RandSlv) возвращает значение типа std_logic_vector.

В связи с тем что входные сигналы генерируются псевдослучайным образом, необходим механизм, позволяющий отследить, какие состояния s₁…s₆ и какие значения сигналов a, b появились (отработали) на входе операционного блока. Для этого используется переменная CovCrossSAB типа CovPType (строка 29). В строках 33–39 производится настройка модели покрытия в соответствии с требованиями, которые были указаны выше: 6 корзин для состояний автомата и по 5 корзин для сигналов a, b. Сбор отработанных значений переменных st_cur, a, b проводится с помощью метода icover (строки 69–72).

Ограничим выполнение тестирующей программы генерацией 10 000 входных псевдослучайных векторов. Чтобы отследить момент, когда все требуемые диапазоны переменных будут покрыты, используется метод IsCovered, который возвращает значение true, если все корзины покрыты. В строках 78–80 осуществляется данная проверка и происходит выход из цикла генерации тестовых векторов, если все корзины покрыты. Далее осуществляется вывод результатов покрытия. Метод WriteBin выводит в консоль статистику по всем корзинам для переменной CovCrossSAB. Метод WriteCovHoles выводит список непокрытых корзин при их наличии.

Выполним тестирующую программу (см. листинг 1), указав, что для целей функционального покрытия будет использоваться не более 10 000 случайно генерируемых тестовых наборов. После выполнения моделирования видно (см. рис. 1), что автомат fsm проходил различные циклы по графу переходов: состояние s₁ автомат прошел 2488 раз, состояние s₂ – 2374 раз и т.д. Всего пройдено состояний 2488+2374+883+2043+1174+1006=9968, что меньше 10 000. Это связано с тем, что произошел дополнительный выход (строка 79) из цикла, так как выполнилось условие if CovCrossSAB.IsCovered then в строке 78, заключающееся в том, что все корзины оказались покрытыми. В результате моделирования выяснилось, что выполнено требуемое функциональное покрытие VHDL-модели устройства system. Когда моделирование закончилось, в окне Transcript системы Questa Sim появилась информация о том, как заполнены все перекрёстные корзины.

Например, для состояния s₁ во фрагменте

# %% WriteBin: State/A/B cross coverage
# %% Bin:(0) (0) (0)   Count = 13 AtLeast = 1 Weight = 1
# %% Bin:(0) (0) (1 to 4) Count = 41 AtLeast = 1 Weight = 1
# %% Bin:(0) (0) (5 to 9) Count = 41 AtLeast = 1 Weight = 1
# %% Bin:(0) (0) (10 to 14) Count = 48 AtLeast = 1 Weight = 1
# %% Bin:(0) (0) (15)   Count = 7
AtLeast = 1 Weight = 1

отчёта о функциональном покрытии указывается, что в состоянии s₁ операция and над операндами a, b [4] выполнялась 13 раз для нулевых значений операндов, 41 раз при нулевом значении операнда a значение операнда b попадало в корзину 2 (диапазон значений 1…4) и т.д. При равномерном распределении вероятностей генерации операндов a, b требуется длинная последовательность из 9968 тестовых наборов. Это происходит из-за того, что при равномерном распределении вероятности значения 0 и 15 выпадают в разы реже, чем значения из диапазонов (корзин), состоящих из четырёх либо пяти значений. Поэтому целесообразно использовать метод DistValSlv генерации псевдослучайных чисел с заданным распределением вероятностей:

A <= RndA.DistValSlv(
((0,5),
(1,1),(2,1),(3,1),(4,1),
(5,1),(6,1),(7,1),(8,1),(9,1),
(10,1),(11,1),(12,1),(13,1),(14,1),
15,5)), A’length);
                                             
B <= RndB.DistValSlv(
((0,5),
(1,1),(2,1),(3,1),(4,1),
(5,1),(6,1),(7,1),(8,1),(9,1),
(10,1),(11,1),(12,1),(13,1),(14,1),
(15,5)), B’length);

В этом случае, если заменить строки 74–75 данными операторами, общее число тестовых векторов, необходимых для покрытия заданных корзин, сокращается на порядок (см. рис. 4) и моделирование заканчивается значительно быстрее.

Естественно, можно подготовить тестирующую программу для функционального покрытия только операционного блока либо только управляющего автомата, заменяя тем самым имеющиеся возможности системы моделирования. Как показано в [3], генерация тестирующих наборов (входных операндов операционного блока и входных сигналов управляющего блока) может осуществляться по различным законам распределения: равномерный закон распределения, распределение с преобладанием малых значений, распределение с преобладанием больших значений, нормальный закон распределения, распределение Пуассона.

Заключение

Как показывает практика верификации, моделирование с покрытием кода и функциональная верификация позволяют найти подавляющее число ошибок в моделях цифровых устройств, состоящих из управляющего и операционного блоков, что значительно сокращает общее время верификации сложных систем, в состав которых входят такие устройства.

Литература

1. Чэнь М., Цинь К., Ку Х.-М., Мишра П. Валидация на системном уровне. Высокоуровневое моделирование и управление тестированием. – М.: Техносфера, 2014. – 296 с.
2. Open source VHDL verification methodology. User’s Guide Rev. 2016.11: http://osvvm.org/downloads.
3. Бибило П.Н., Авдеев Н.А. Моделирование и верификация цифровых систем на языке VHDL. – М.: Ленанд, 2017. – 344 с.
4. Авдеев Н., Бибило П. Верификация VHDL-описаний цифровых устройств, представленных в виде композиции управляющего и операционного блоков. Часть 1. Верификация на основе покрытия VHDL-кода. Современная электроника. 2018. № 2.