Характеристики обнаружения последетекторной межпериодной обработки с обеляющим фильтром

Чухломин Иван, Файзулин Наиль

В статье рассмотрены характеристики обнаружения последетекторной адаптивной межпериодной обработки сигналов в шуме и коррелированной помехе. Определены параметры предпороговой статистики. Установлено, что когерентность сигнала несущественно влияет на характеристики обнаружения.

78 0 0

печатать Статья в PDF (592 КБ)

Введение

Задача обнаружения сигнала в коррелированной помехе решается в два этапа: «обеление» помехи и затем обнаружение сигнала на фоне белого шума. «Обеление» помехи осуществляется цифровым режекторным фильтром, весовые коэффициенты которого определяются обратной корреляционной матрицей помехи. В реальных условиях корреляционная матрица помехи неизвестна, поэтому производится адаптивная обработка, предполагающая оценку корреляционной матрицы помехи и её обращение [1].

Практическая реализация такой обработки затруднительна, особенно при обработке комплексной входной выборки помехи и сигнала.

Последетекторная межпериодная обработка (МПО) использует выходные сигналы амплитудного детектора, и вычислительные операции производятся с действительными числами, что упрощает реализацию обработки. Структура МПО представляет собой адаптивный матричный обеляющий фильтр (ОФ) и блок скалярного перемножения выходных сигналов фильтра [2].

Целью статьи является определение характеристик обнаружения последетекторной МПО при различных моделях сигнала и помехи.

Модель сигнально-помеховой обстановки

Сигнал и помеха полагаются взаимно-независимыми гауссовыми (до детектора) случайными векторами размерности М с корреляционной матрицей (КМ) межпериодных флуктуаций импульсов пачки М:

КМ шума:

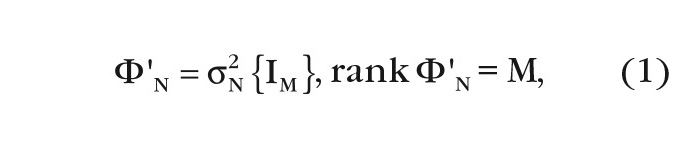
где σ²_N – мощность шума, {I_M} – единичная матрица М × М;
КМ помехи:

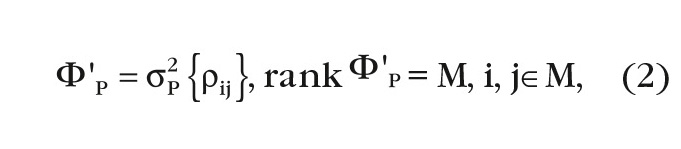
где σ²_P – мощность шума, ρ_ij – коэффициент корреляции;
КМ некогерентного сигнала:

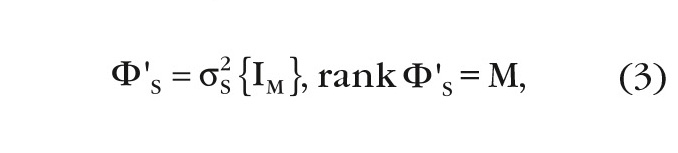
где σ²_S – мощность сигнала;
КМ когерентного сигнала:

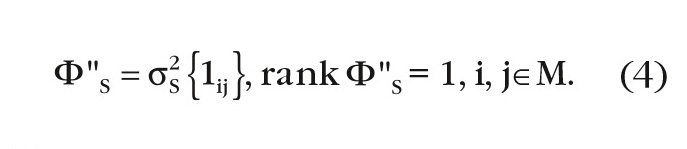
Методика расчётов

Для определения D при заданной величине F производится вычисление закона распределения выходного процесса МПО, который определяется выражением:

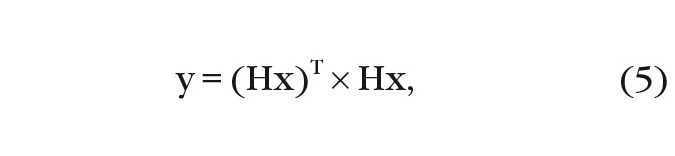
где x – M-мерный вектор пачки входного процесса ОФ, H – матричная импульсная характеристика (МИХ) ОФ, размерности M × M.

МИХ H определяется из соотношения:

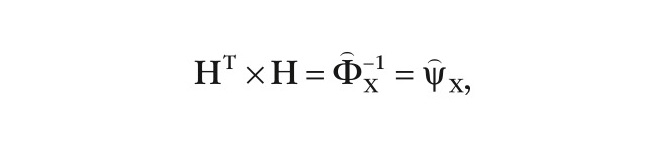
и представляет собой «корень» матрицы ^ˆψ_Χ, обратной КМ ^ˆΦ_Χ.

Вычисление ^ˆΦ_Χ производится путём расчёта КМ-процесса после амплитудного детектора в соответствии с формулой [3]:

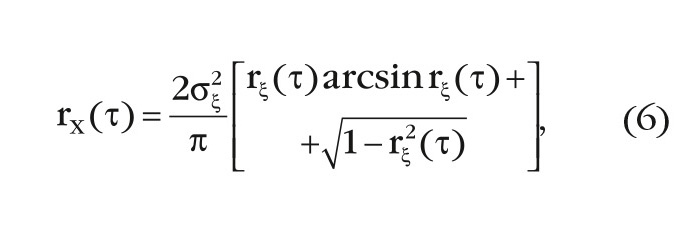
где σ²_ξ, r_ξ (τ)– параметры корреляционной функции процесса на входе амплитудного детектора.

Значения r_Χ(τ), взятые при отсутствии сигнала, являются элементами обучающей матрицы ^ˆΦ_Χ, определяющей МИХ H.

Обнаружение при некогерентном сигнале

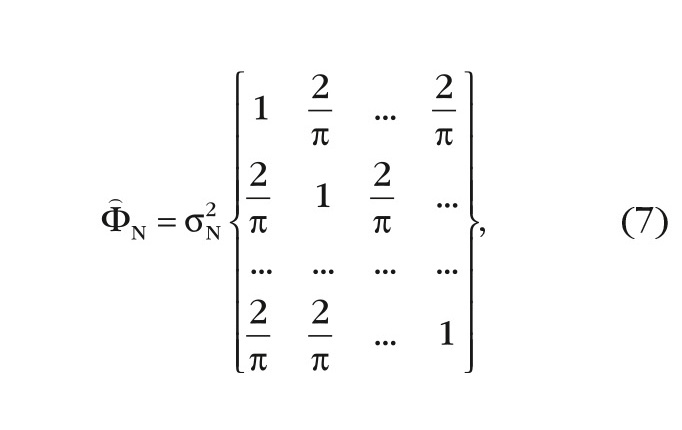
Обучающая матрица ^ˆΦ_Χ размерности M × M, полученная из Φ′_N в соответствии с (6) имеет вид:

КМ шума на выходе ОФ:

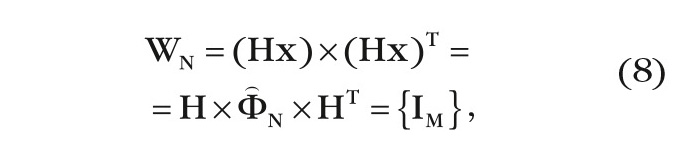
так как ^ˆΦ_N=H^-1×(H^-1)^T.

Выход МПО есть сумма квадратов выходных сигналов ОФ. В соответствии с (8) эти сигналы представляют М взаимонезависимых гауссовых величин с нулевым математическим ожиданием и одинаковой единичной дисперсией, и плотность вероятности выходного шума МПО подчиняется χ²-распределению [3]:

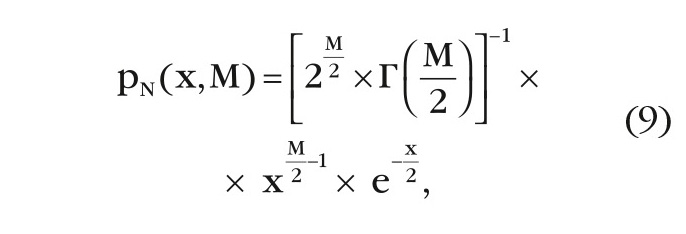
Где Г( ) – гамма-функция.

Вероятность ложной тревоги F равна:

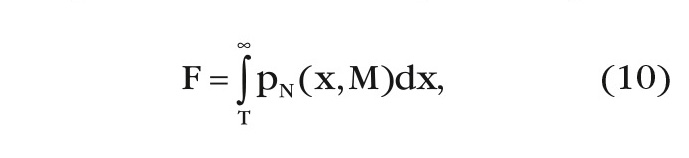
где T – пороговый уровень.

Из (10) следует, что F зависит только от М и Т.

Для смеси сигнал + шум:

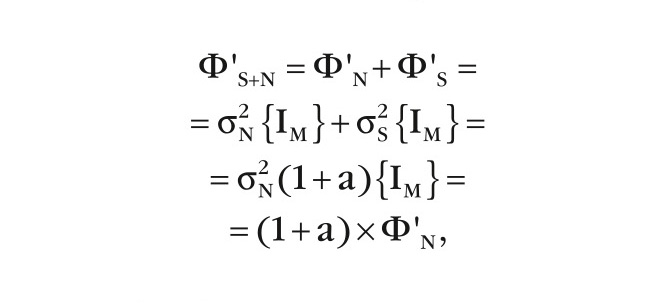
где a=σ_S²/σ_N² – отношение сигнал / шум, отсюда следует, что КМ смеси сигнал + шум равна:

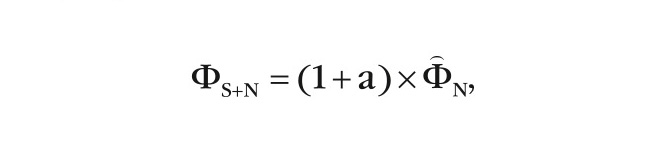
таким образом, КМ Ф_S+N отличается от ^ˆΦ_N только величиной дисперсии, увеличенной в (1 + a).

КМ смеси сигнал + шум на выходе ОФ равна:

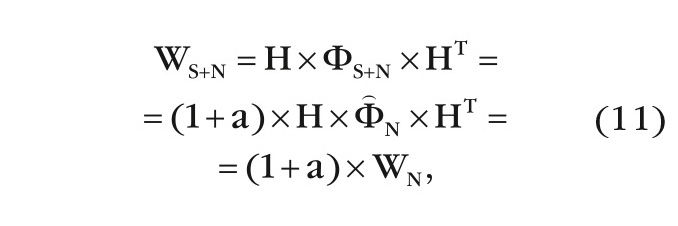
и, следовательно, выходные сигналы ОФ также являются М взаимонезависимыми гауссовыми случайными величинами с нулевым математическим ожиданием и одинаковой дисперсией (1 + а), поэтому плотность вероятности выходного сигнала МПО имеет вид [3]:

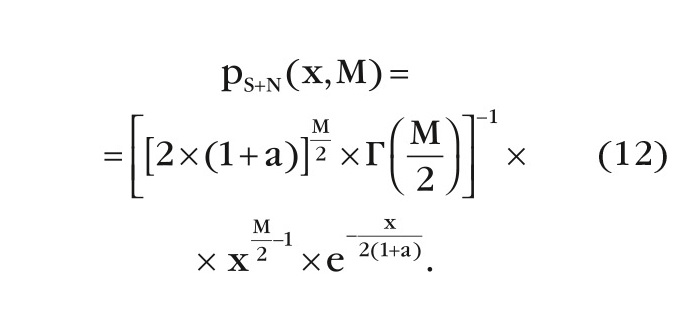
Вероятность правильного обнаружения D равна:

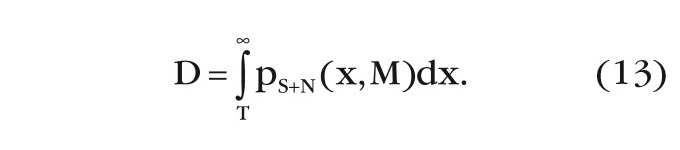
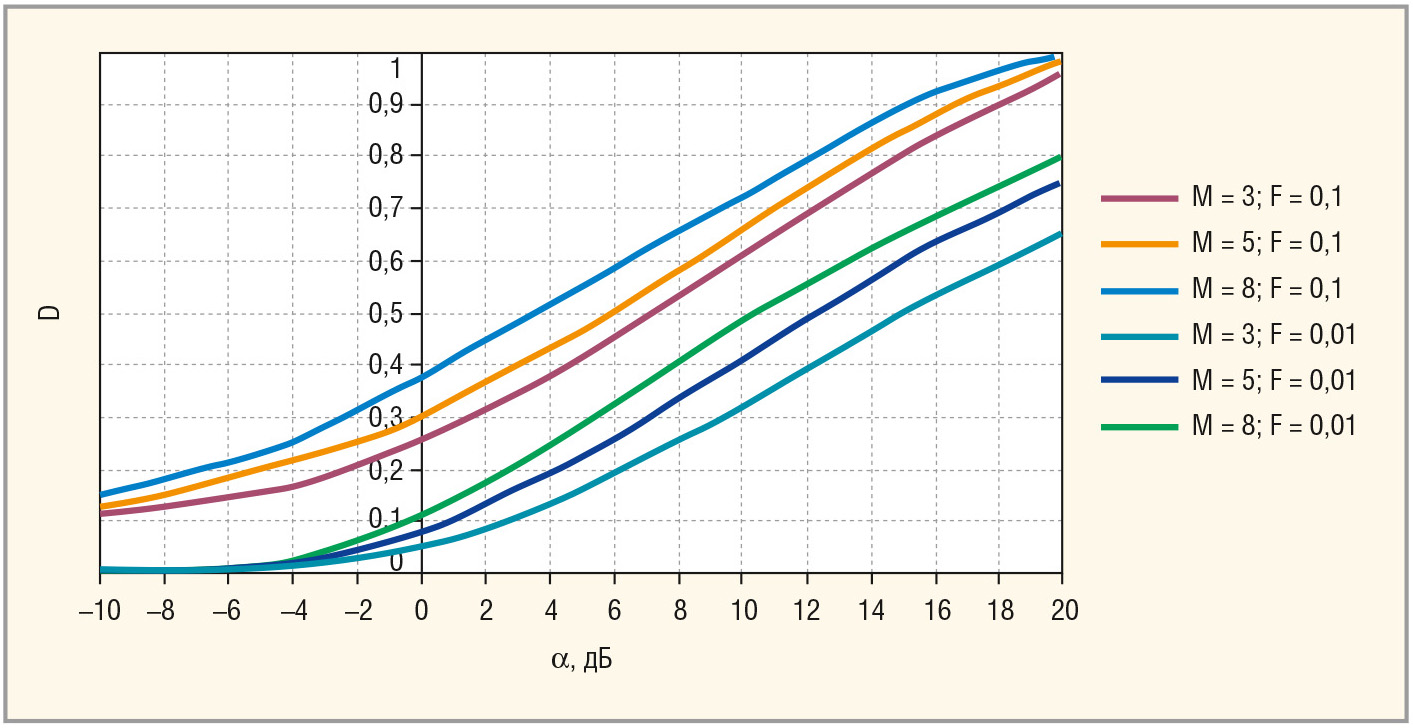
Характеристики обнаружения, рассчитанные в соответствии с (13), приведены на рисунке 1.
Рис. 1. Характеристики обнаружения (некогерентный сигнал)

Обнаружение при когерентном сигнале

Обучающая матрица ^ˆΦ_N остаётся без изменений и имеет вид (7), и, следовательно, плотность вероятности выходного шума МПО определяется выражением (9).

Для смеси сигнал + шум:

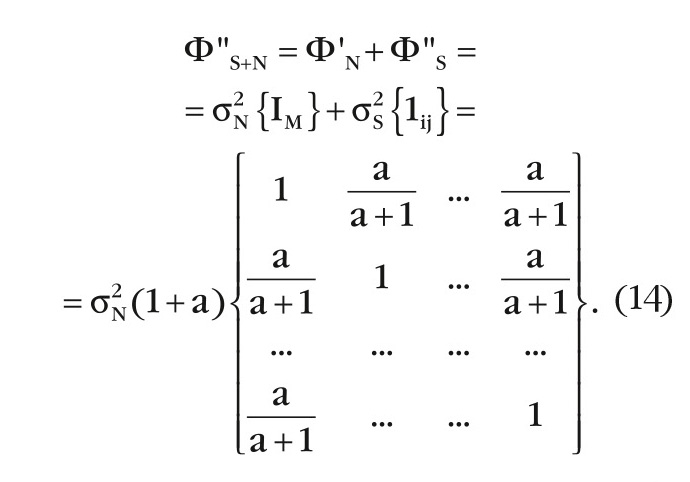
В результате преобразования (6) матрица Ф_S+N содержит значения π/2 в главной диагонали, и значения (a/(a+1))arcsin(a/(a+1))+√1−(a/(a+1))² для недиагональных элементов. Таким образом, Ф_S+N существенно отличается от Ф_N и плотность вероятности смеси сигнал + шум не может быть описана выражением (12).

Аналитическое определение плотности вероятности смеси сигнал + шум на выходе МПО не представляется возможным, и выражения для p_S+N(x,M) получены по результатам имитационного моделирования. Обработка результатов моделирования показывает, что плотность вероятности процесса на выходе МПО с высокой степенью точности аппроксимируется логнормальным распределением вида

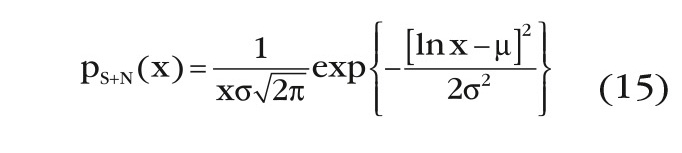
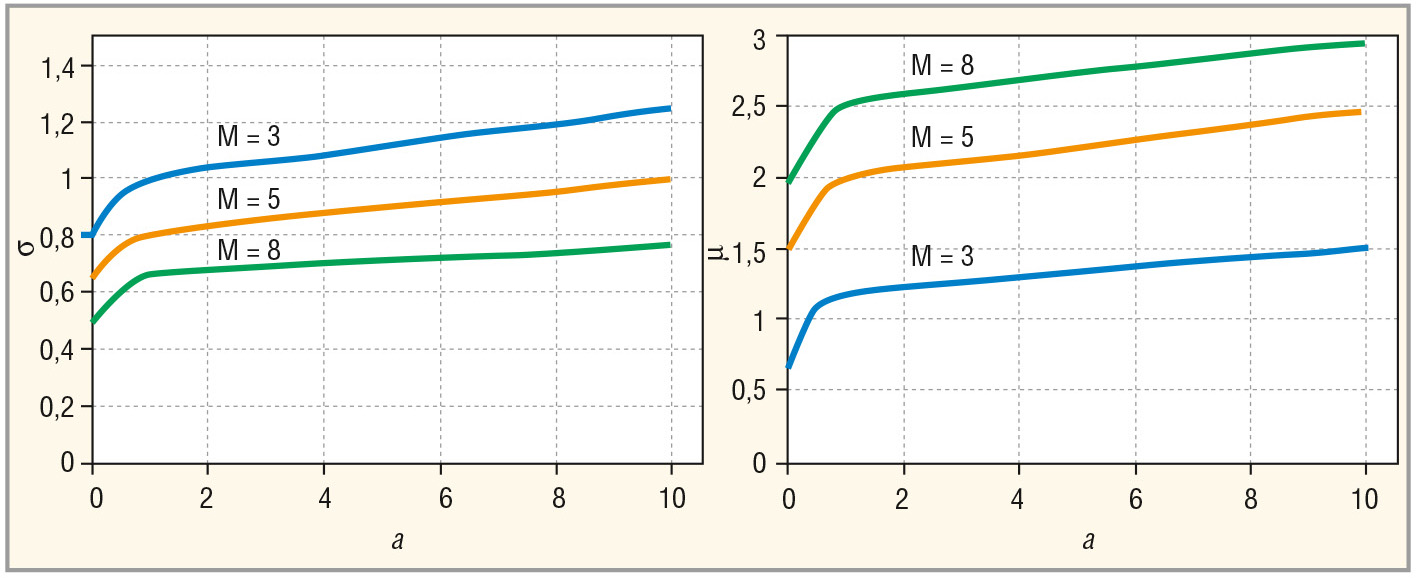
с параметрами µ и σ, зависящими от М и а, приведёнными на рисунке 2.
Рис. 2. Параметры распределения Рs + n(X)

Вероятность ложной тревоги F и пороговый уровень T определяются выражением (10), а вероятность правильного обнаружения D определяется выражением

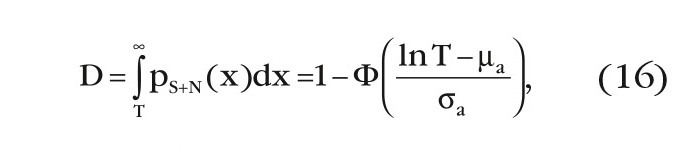
где

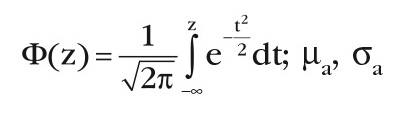
– параметры распределения при а ≠ 0 из рисунка 2.

Характеристики обнаружения, рассчитанные в соответствии с (16), приведены на рисунке 3.
Рис. 3. Характеристики обнаружения (когерентный сигнал)

Обнаружение в коррелированной помехе

Обучающая матрица ^ˆФ_S+N определяется преобразованием (6) КМ ^ˆФ′_S+N суммы шума с помехой:

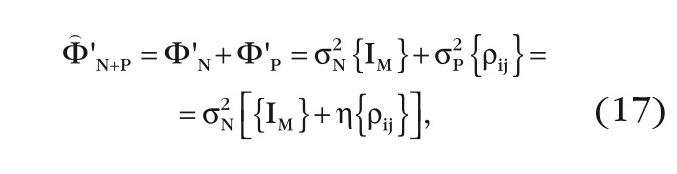
где η=σ²_P/σ²_N – отношение помеха / шум, ρ_ij – коэффициенты экспоненциальной корреляционной функции.

В результате матрица ^ˆФ_S+N имеет значения π/2 в главной диагонали и значения d_ij для недиагональных элементов

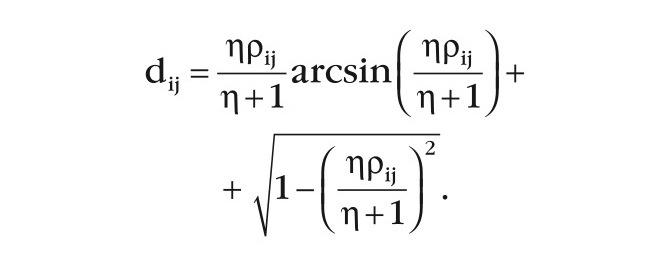
Так как при отсутствии сигнала КМ входного процесса МПО равна КМ ^ˆФ_S+N, то КМ выходного процесса МПО равна {I_M} и закон распределения его имеет вид (9).

В работе [4] показано, что при взаимодействии сигнала с коррелированной помехой когерентность пачки не имеет значения.

КМ смеси сигнал + помеха + шум при σ²_P >>σ²_S может быть представлена в виде [5]:

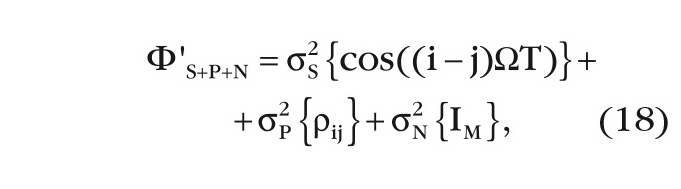
где Ω – разность допплеровских частот помехи и сигнала, Т – период зондирования.

В результате преобразования (6) КМ Ф_S+P+N имеет значения π/2 в главной диагонали и значения c_ij для недиагональных элементов матрицы:

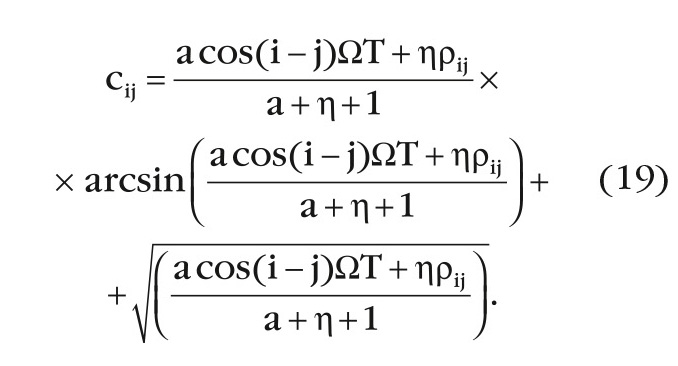
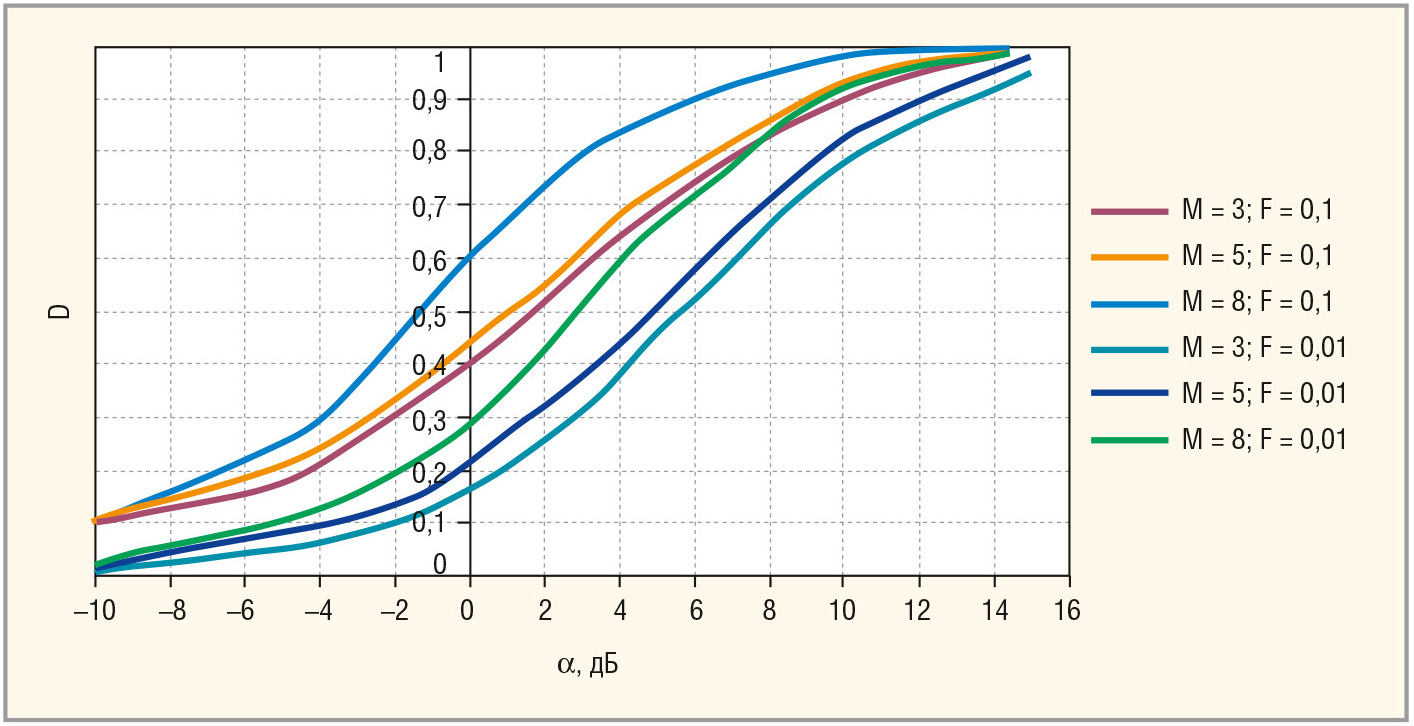
Результаты моделирования показывают, что и в этом случае плотность вероятности процесса на выходе МПО соответствует логнормальному распределению (15) с параметрами µ и β, зависящими от М, а, η, ΩT, ρ_ij, γ (ΩT = π; а = 10 дБ; γ=σ²_P/σ²_N; ρ_ij = 0,99^i–j; M = 3, 5, 8) и приведёнными на рисунке 4.

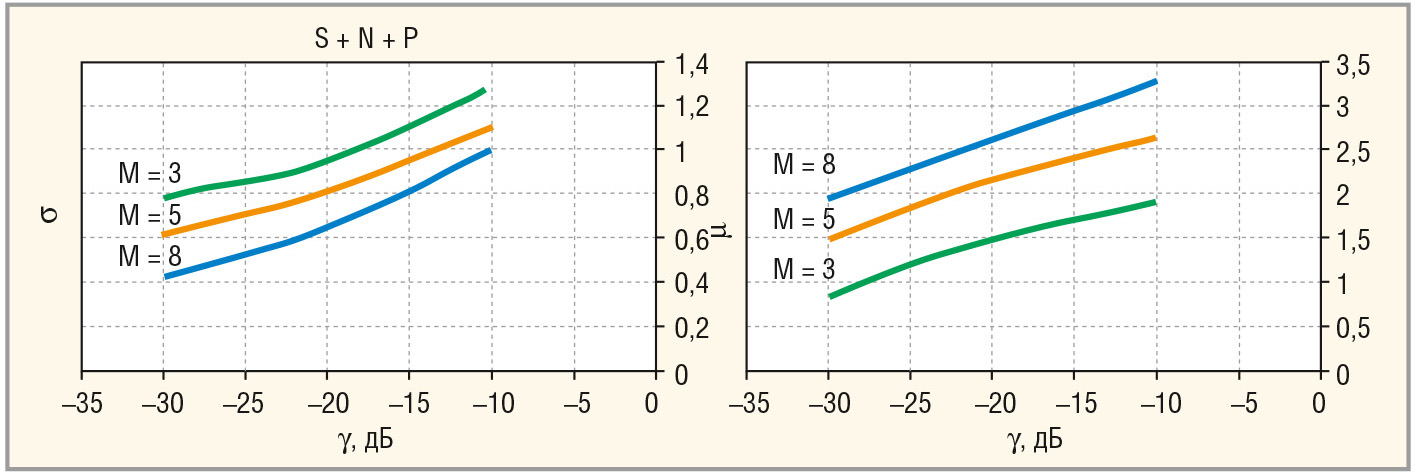
Вероятность ложной тревоги F и пороговый уровень T также определяются выражением (10), а вероятность правильного обнаружения D равна:

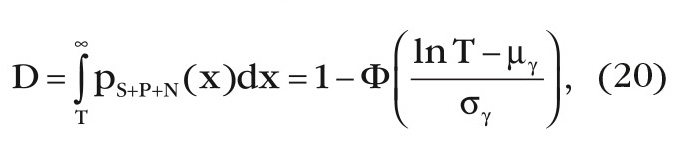
где µ_γ и β_γ – параметры распределения (15) при γ ≠ 0 из рисунка 4.

Характеристики обнаружения, рассчитанные в соответствии с (20) приведены на рисунке 5.
Рис. 5. Характеристики обнаружения (коррелированная помеха)

Заключение

Последетекторная МПО с обеляющим фильтром обеспечивает обнаружение сигнала в коррелированной помехе.

Отличительными особенностями последетекторной МПО является стабильный уровень ложных тревог, не зависящий от параметров распределения шума и помехи, и некритичность к когерентности сигнала.

Последнее обстоятельство особенно важно для радиолокационных станций с некогерентными сигналами.

Литература

Бартенев В.Г. Квазиоптимальные адаптивные алгоритмы обнаружения сигналов. Современная электроника. 2011. №2.
Леховицкий Д.И., Кириллов И.Г., Бурковский С.И. Особенности междупериодной обработки сигналов на фоне пассивных помех в некогерентных импульсных РЛС. Журнал радiоелектроннi i комп’ютернi системи. 2005. №2 (10). С. 51–57. www.khai.edu/csp/nauchportal/Arhiv/REKS/2005/REKS205/pdf/Lehovick.pdf.
Тихонов В.И. Статистическая радиотехника. 2-е изд., перераб. и доп. М. Радио и связь. 1982. С. 624.
Морская радиолокация. Под ред. Винокурова В.И. Л. Судостроение. 1986. С. 256.
Чухломин И.Е., Файзулин Н.А. Эффективность некогерентной межпериодной обработки на основе обеляющего фильтра. IX Всероссийская конференция «Радиолокация и радиосвязь». ИРЭ РАН. Москва. 2015.