Реализация адаптивной нелинейной цифровой фильтрации на программируемых логических интегральных схемах

Оптимальные алгоритмы обработки цифровых сигналов основываются на использовании статистических моделей сигналов и шумов, базирующихся на концепциях линейности, стационарности и нормальности, которые не всегда реализуемы на практике. Решение проблемы может заключаться в использовании адаптивных фильтров (АФ), позволяющих системе цифровой обработки сигналов подстраиваться под статистические свойства обрабатываемых сигналов без применения соответствующих моделей.

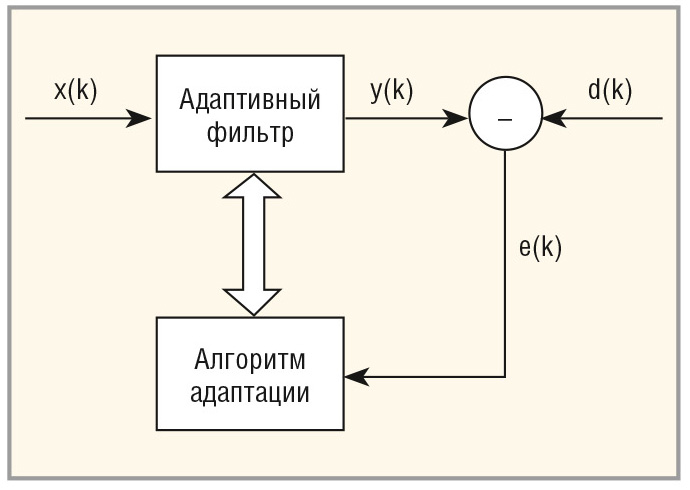
Адаптивная фильтрация сигналов имеет прикладное значение для информационных технологий, радиотехники, цифровой и аналоговой связи. Обобщённая структура АФ приведена на рисунке 1 (входной сигнал x(k), выходной сигнал y(k), образцовый сигнал d(k), сигнал ошибки e(k), k – порядковый номер временно¢го интервала фильтрации).

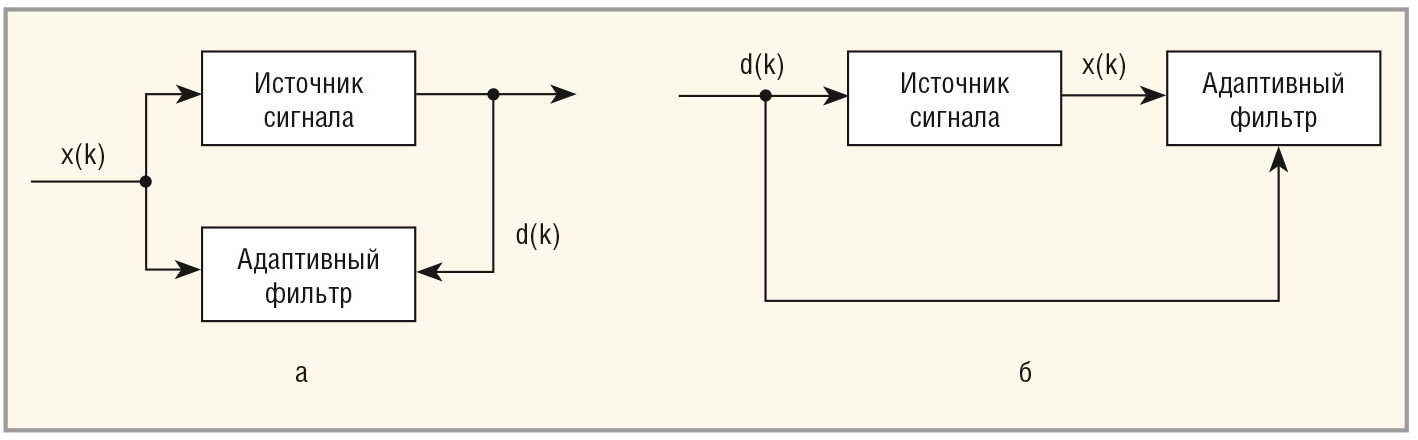
К задачам, решаемым с помощью АФ, относятся идентификация систем, подавление шума, компенсация искажений сигнала и так далее [1–4]. При решении задачи идентификации системы, то есть определении её характеристик, возможны прямая или обратная идентификация (см. рис. 2). При решении задачи прямой идентификации входной сигнал АФ приближается к образцовому сигналу. Разностным сигналом между образцовым и выходным сигналами АФ является очищенный от шума сигнал (см. рис. 2а). Поскольку информационный сигнал при передаче по каналу цифровой связи претерпевает искажения, приводящие к возникновению ошибок при его приёме, то для снижения вероятности ошибок необходимо компенсировать влияние канала связи, решая задачу обратной идентификации (см. рис. 2б).

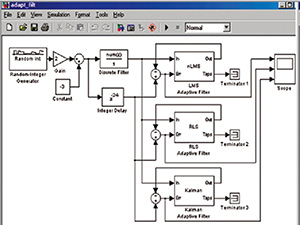
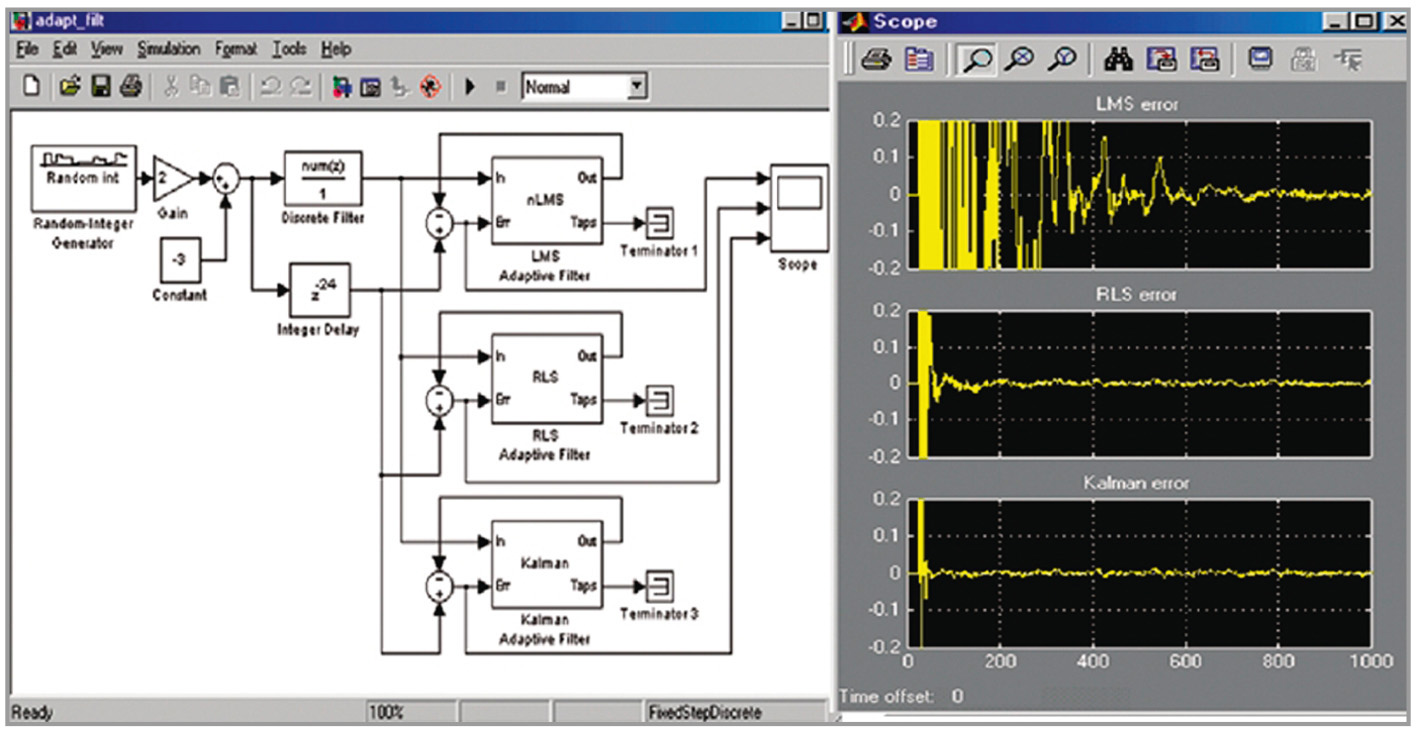
Наиболее распространёнными являются следующие цифровые адаптивные фильтры: на базе метода наименьших квадратов – LMS (Least Mean Square), на основе рекурсивного метода наименьших квадратов – RLS (Recursive Least Square), фильтры Калмана, позволяющие создавать системы цифровой обработки сигналов, успешно функционирующие при наличии шумов и помех с неизвестными заранее свойствами. Для оценки влияния параметров алгоритмов адаптации АФ на точность оценивания и достоверность приёма данных рекомендуется использовать метод имитационного моделирования. Моделирование процесса адаптивной обработки сигнала можно реализовать с использованием MATLAB: в пакете расширения Filter Design с применением набора блоков DSP Blockset среды моделирования Simulink, имеющей функции и блоки, реализующие наиболее распространённые алгоритмы адаптивной фильтрации [5]. Исследованиями установлено [6, 7], что сигнал ошибки для алгоритма фильтра LMS сходится медленнее и даёт большие остаточные шумы, в то время как алгоритмы фильтров RLS и Калмана обеспечивают сходные показатели лучшего качества (см. рис. 3).

Широко применяемый при цифровой обработке сигналов алгоритм линейного АФ Калмана (АФК) основывается на представлении пространства его состояний. Применяется также для полной характеристики поведения цифровой системы использования переменных, сохранённых в векторе его состояния. АФК обновляет вектор состояния линейно и рекурсивно с помощью матрицы переходов и оценки процесса шума. Цель линейного АФК – минимизировать дисперсию оценки истинного состояния векторного стохастического процесса x_k в момент k, изменяющегося во времени и описываемого на основе рекурсивного метода разностным уравнением:

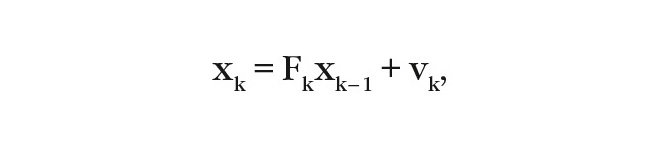
где F_k – матрица перехода, v_k – случайный вектор (шум процесса), имеющий нормальное распределение с корреляционной матрицей.

Наблюдаемому линейно преобразованному процессу соответствует уравнение:

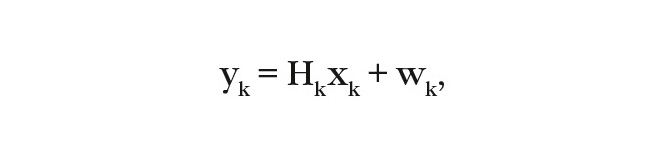
где H_k – матрица наблюдений, w_k – шум наблюдения, представляющий собой случайный вектор, имеющий нормальное распределение с корреляционной матрицей.

Использование АФК для линейной фильтрации ориентировано на применение линеаризованной упрощённой математической модели динамической системы. Такой фильтр обладает наименьшей среднеквадратической ошибкой. Однако должны выполняться следующие условия: шум является «белым» и распределяется по нормальному закону, математическое ожидание шумов равно нулю, отсутствуют корреляции между шумами и перекрёстные связи между фазовыми координатами. Перечисленные ограничения на практике часто нарушаются. Если шумы «цветные», то необходимо синтезировать цифровой формирующий фильтр. «Белый» шум при пропускании через него будет обладать спектральной характеристикой, эквивалентной или близкой к исходной.

Для систем цифровой обработки сигналов, уравнения динамики и наблюдений которых содержат нелинейные функции от фазовых координат, а также при наличии перекрёстных связей между фазовыми координатами, рекомендуется использовать адаптивный нелинейный (расширенный) фильтр Калмана – РФК (Extended Kalman Filter, EKF). При использовании РФК процесс фильтрации описывается нелинейными стохастическими разностными уравнениями с необходимостью на каждом шаге итераций вычислять Якобиан – матрицу частных производных от фазовых координат. То есть, в РФК линеаризация производится путём вычисления Якобиана:

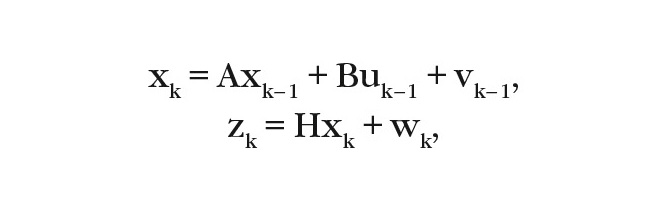
где u_k-1 – вектор управляющих воздействий, z_k – выходной вектор, A – матрица эволюции процесса/системы, воздействующая на вектор состояния x_k–1 в момент k–1, B – матрица управления, прикладываемая к вектору управляющих воздействий u_k-1, v_k-1 – случайный вектор (шум процесса) в момент k–1, имеющий нормальное распределение с корреляционной матрицей, H – матрица наблюдений, связывающая истинный вектор состояния и вектор произведённых наблюдений, w_k – шум наблюдения, представляющий собой случайный вектор, имеющий нормальное распределение с корреляционной матрицей.

Приближенное к линейному состояние векторов x_k и z_k можно записать в виде:

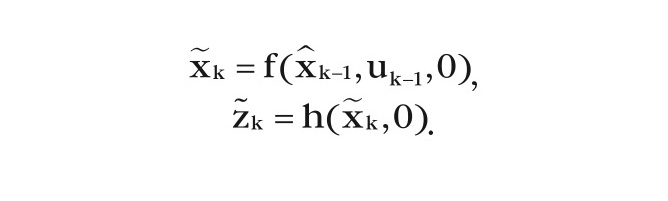
Тогда оценки процесса с нелинейной разностью измерений и отношений с линеаризуемой оценкой будут иметь вид:

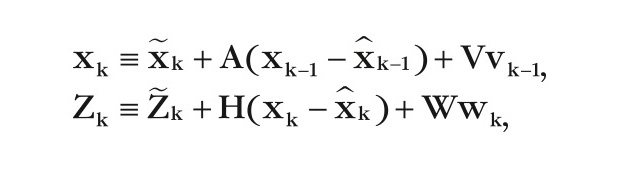
где ˜x_k и Z_k – приблизительные состояние и измерение векторов х_к и z_к, ˜x_k – апостериорная оценка состояния процесса на этапе k, ˆx_k-1 – апостериорная оценка состояния процесса на этапе k–1, А – матрица Якоби частных производных f по х, v_k-1 – случайный вектор (шум процесса) в момент k–1, имеющий нормальное распределение с корреляционной матрицей, V – матрица Якоби частных производных f по v, Н – матрица Якоби частных производных h по х, w_k – шум наблюдения, представляющий собой случайный вектор, имеющий нормальное распределение с корреляционной матрицей, W – матрица Якоби частных производ-ных h по w.

Архитектура РФК для оценок процесса с нелинейной разностью измерений и отношений с линеаризуемой оценкой может быть реализована на основе матричного процессора (см. рис. 4).

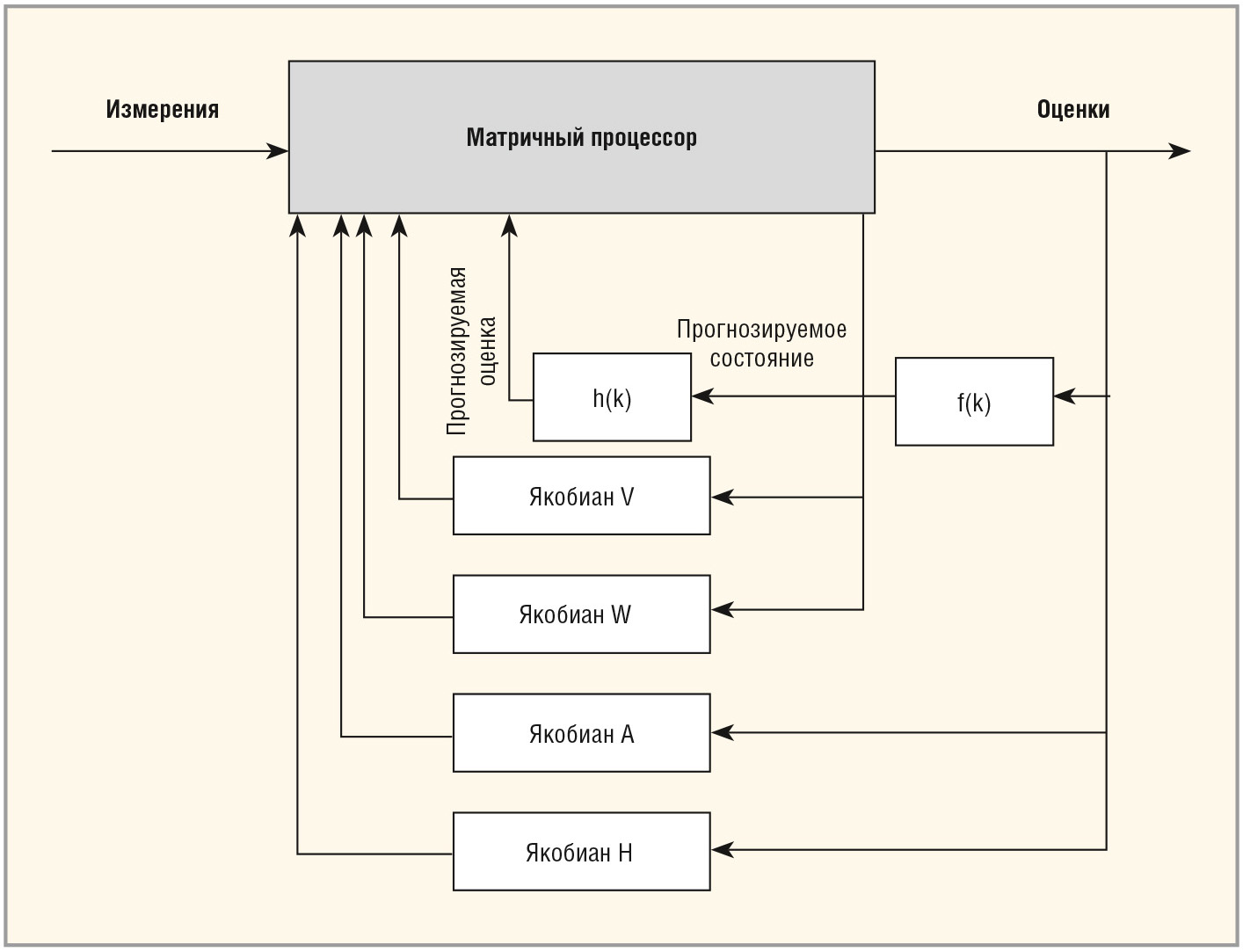
Реализация РФК может быть осуществлена на основе аппаратных средств или программного обеспечения. При этом требуется использовать существенные вычислительные мощности, что связано с выполнением нескольких матричных операций, в том числе обращения матрицы, целочисленных арифметических операций (операций в формате с фиксированной запятой).

Конвейерная обработка и параллельные вычисления программируемых логических интегральных схем (ПЛИС) часто позволяют проектам достигать высокой скорости обработки сигналов при низком энергопотреблении – быстрее, чем усовершенствованная машина RISC (ARM), обработчик цифровых сигналов (DSP) или специализированная интегральная схема (ASIC). Кроме того, интеграция в ПЛИС основных логических блоков со встроенными микропроцессорами и периферийными устройствами делает проект на ПЛИС более гибким и адаптируемым, существенно уменьшая время на проектирование системы.

Значительная часть адаптивного алгоритма РФК может быть реализована на ПЛИС с параллельной аппаратной обработкой и обработкой данных в реальном времени. Алгоритм фильтра состоит из нелинейной модели неизменной части системы.

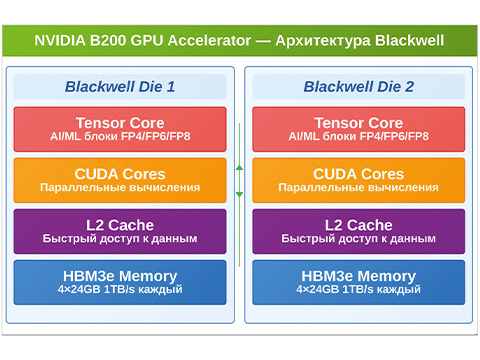
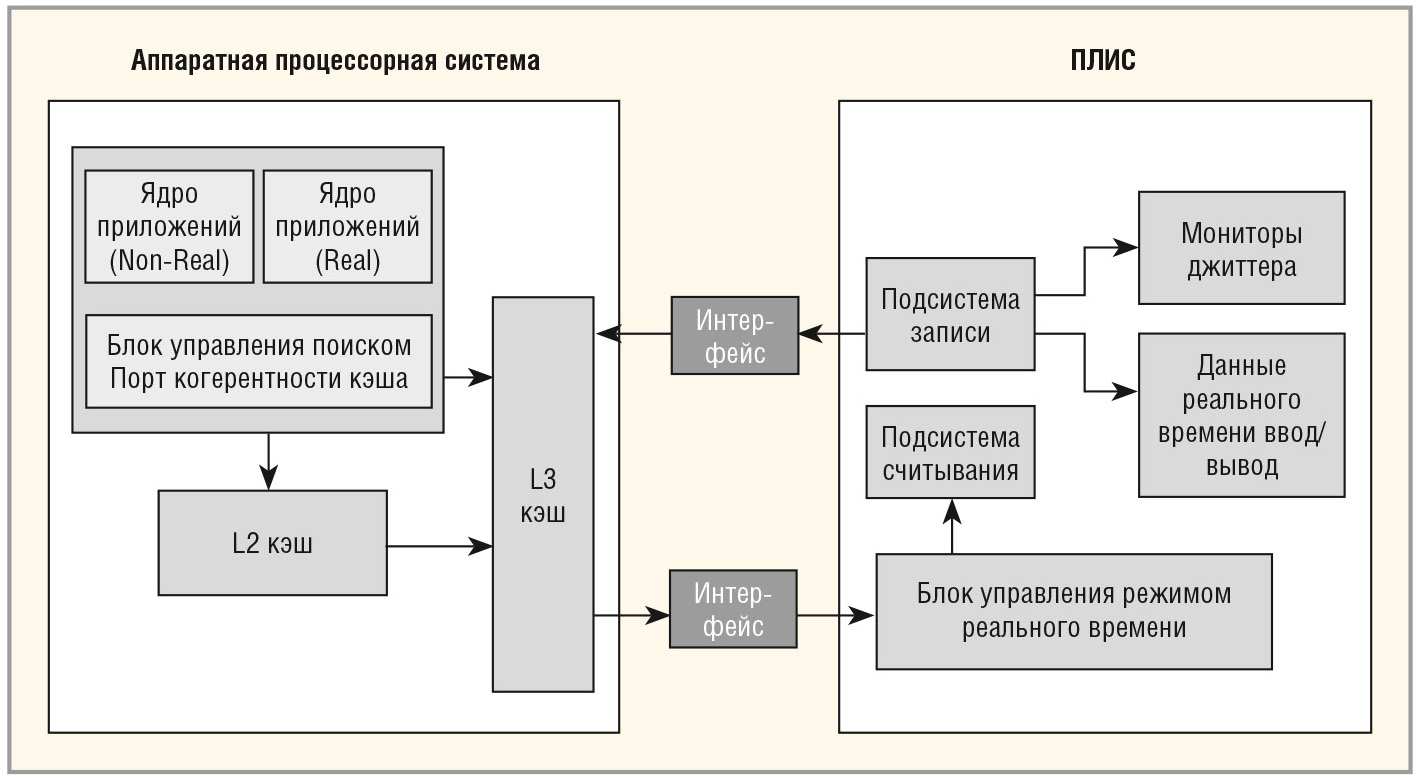
Расширенный фильтр Калмана (см. рис. 4) может быть реализован аппаратно в приложении матричного процессора и ПЛИС производства Altera [8] на основе изготовленного по 28-нм технологии встроенного двухъядерного процессора ARM Cortex-A9 и ПЛИС Cyclone V или Arria V (см. рис. 5). Матричные операции РФК реализуются в проекте на ПЛИС с использованием MATLAB для логики фильтра.

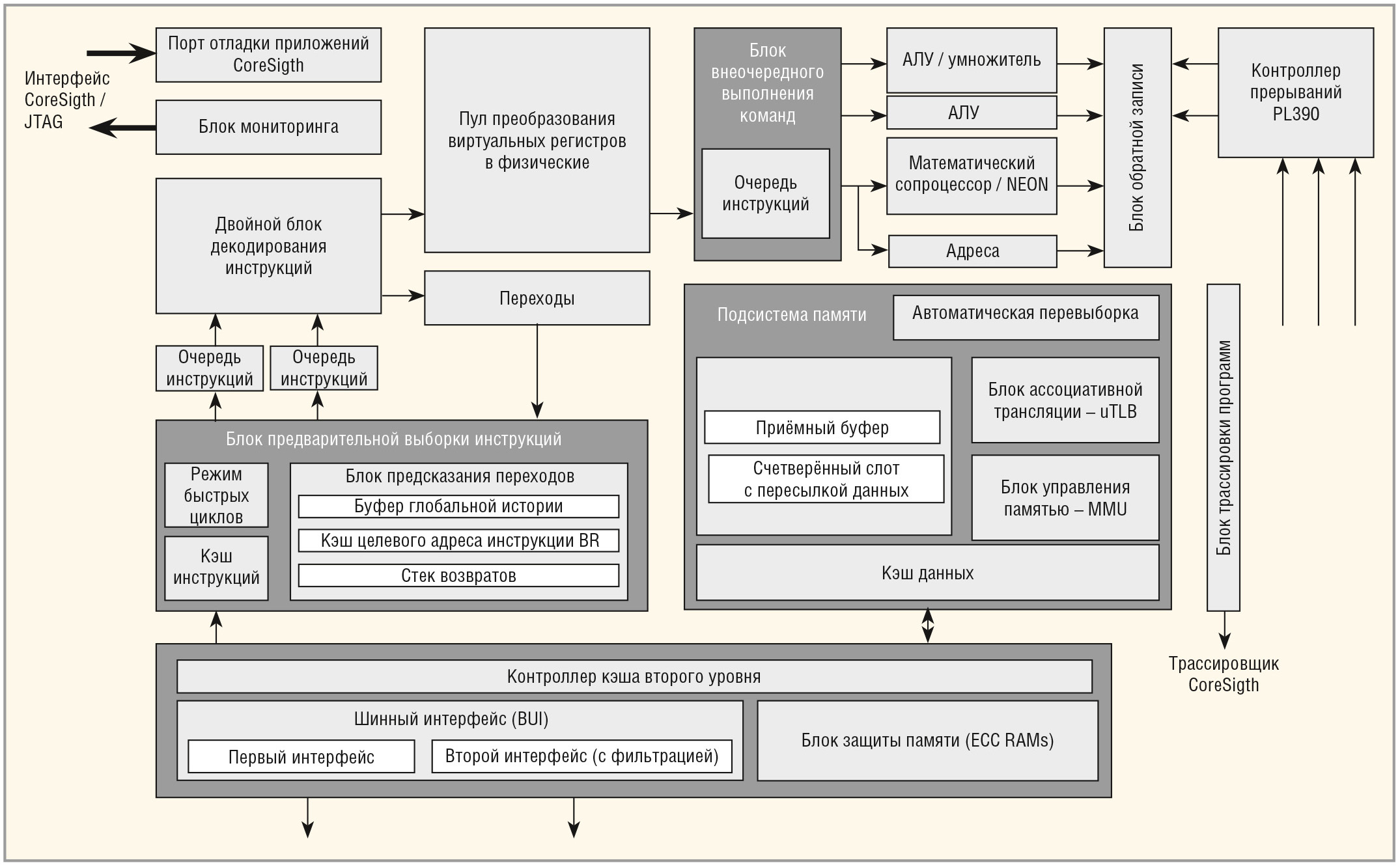
Двухъядерный процессор ARM Сor-tex-A9 позволяет поднять пиковую производительность при одновременной простоте технических решений и возможности контроля потребляемой мощности, как на уровне процессора, так и на уровне системы в целом. Процессор Cortex-A9 (см. рис. 6) обладает возможностью оптимизации производительности приложений, как по скорости выполнения, так и по потребляемой мощности. Он также поддерживается широким спектром отладочных плат и систем разработки прототипов, как в ПЛИС, так и в виде программных средств.

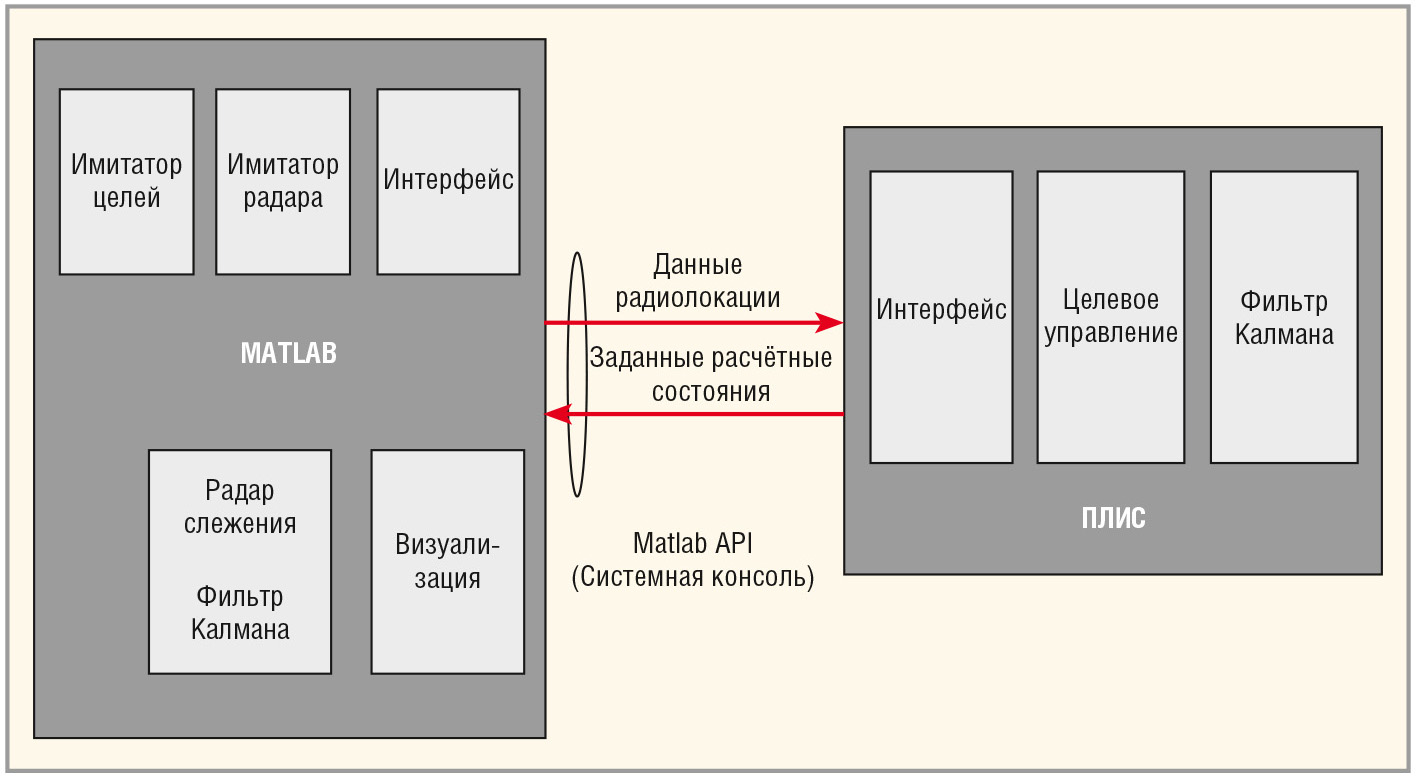
Используя гибридную архитектуру ПЛИС, например, для радиолокационной системы (см. рис. 7), РФК может быть реализован в приложении матричного процессора на базе ядер Cortex-A9 и ПЛИС Cyclone V производства Altera. Основная часть фильт-ра, преимущественно матричные операции различного размера, в целях максимальной производительности реализуется в ПЛИС с использованием HDL-описания структуры фильтра на языке Verilog для его функциональной верификации.

Таким образом, реализация расширенного (нелинейного) фильтра Калмана в целях адаптивной цифровой фильтрации может с успехом осуществляться на основе матричного процессора и ПЛИС.

Литература

1. Уидроу Б., Стирнз С. Адаптивная обработка сигналов. Пер. с англ. 1989. М. Радио и связь. 440 с.
2. Коуэн К. Ф. Н. Адаптивные фильтры. Пер. с англ. Под ред. Коуэна К. Ф. Н. и Гранта П. М. 1988. М. Мир. 392 с.
3. Glentis G.O., Berberidis K., Theodoridis S. Efficient Least Squares Adaptive Algorithms for FIR Transversal Filtering. IEEE Signal Processing Magazine. 1999. V. 16. №4. 13–41 р.
4. Haykin S. Adaptive Filter Theory, 4th edition. Prentice Hall. 2002. 936 p.
5. Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. 2001. СПб. Питер. 448 c.
6. Джиган В.И. Адаптивная фильтрация сигналов: теория и алгоритмы. 2013. М. Техносфера. 528 с.
7. Сергиенко А.Б. Алгоритмы адаптивной фильтрации: особенности реализации в MATLAB/Exponenta Pro: математика приложениях. 2003. №1. 18–28 с.
8. Documentation portal Altera Corporation. www.altera.com/literature.

Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!