Введение

Теория цифровой обработки сигналов и, в частности, цифровых фильтров (ЦФ), основанная на базе со­временной вычислительной техники и достижений классической математики, содержит обширный список литературы. Однако, несмотря на полученные впечатляющие результаты, нельзя сказать, что развитие этой теории завершено. Свидетельством этого является существование большого количества методов анализа и синтеза ЦФ [1–3]. Поэтому задача создания более простых методов при проектировании и эффективных при использовании ЦФ остаётся актуальной и в настоящее время.

Цифровые фильтры могут быть отнесены, говоря в общем, к категории чисто математических систем. Поэтому одни ЦФ имеют в качестве прототипов аналоговые фильтры, другие – не имеют. В общей теории систем для описания физических (и математических) процессов используются различные виды уравнений: интегро-дифференциальные, интегральные, дифференциальные – в обыкновенных и частных производных и ал­гебраические. В некоторых случаях существует непосредственная взаимосвязь между решениями, получаемыми из разных видов этих уравнений. Например, в публикации Вольтерра [2] имеется замечание о том, что решения интегро-дифференциальных уравнений могут быть получены из фундаментальных решений некоторых связанных с ними обыкновенных дифференциальных уравнений. Однако при анализе и синтезе систем управления и их звеньев, а также цифровых и аналоговых фильтров, оказалось, что использование явных решений указанных выше уравнений, как нелинейных, так и линейных, является непродуктивным из-за трудности получения с помощью этих решений зависимостей, непосредственно связывающих процессы на входе и выходе систем. По этой причине для линейных уравнений были разработаны методы получения аналитических решений в виде операторной связи непосредственно между функциями, определяющими процессы на входе и выходе систем. Для этой цели были введены следующие понятия: передаточная функция, переходная и импульсная переходная функция, интеграл свёртки.

Рассмотрим наиболее простой оператор, представляющий собой математическое звено, описываемое линейным алгебраическим равенством:

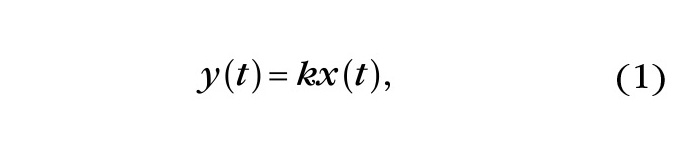
где х(t) и y(t) – функции времени, характеризующие процессы соответственно на входе и выходе звена.

Сами эти функции не обязательно должны быть линейными, но определённые ограничения, связанные с их физической реализацией и требованиями, исходящими из математических методов преобразований, имеют место. Оператор в равенстве (1) является в данном случае просто численным коэффициентом, определяющим амплитудный характер искажения входной функции, проходящей в виде сигнала через рассматриваемое звено. Другими примерами операторов могут служить операторы дифференцирования (p=d/dt) и интегрирования (1/p=∫). Совместно с алгебраическим оператором они образуют дифференциальный оператор, который, воздействуя на гармонический сигнал на входе звена, вызывает амплитудные и фазовые искажения. При этом интенсивность искажения амплитуд и фаз гармоник функционально зависит от частоты. Следует иметь в виду, что в одних случаях воздействие дифференциального оператора рассматривается как искажение сигнала, а в других – как положительное явление, позволяющее проводить необходимые преобразования сигналов. Следует также указать на особо важную роль, которую играют при анализе и синтезе систем гармонические сигналы, построенные на базе особого класса периодических тригонометрических функций – синуса и косинуса. При прохождении через линейные системы они не изменяют своей формы и обладают рядом уникальных свойств (гладкость, определяемая бесконечной дифференцируемостью, инвариантность при сдвиге, ограниченность диапазона значений, совместное представление обоих в единой комплексной экспоненте), которые позволяют им служить в качестве базовых элементов в структуре разложения периодических и непериодических функций. Эти тригонометрические функции, естественным периодом которых является полный угол (2π), могут быть периодически представлены и при любых других единицах измерения аргумента, если соблюдать кратность естественного периода и какого-либо иного, характеризуемого некоторым числом T.

Таким образом, обыкновенное дифференциальное уравнение вида

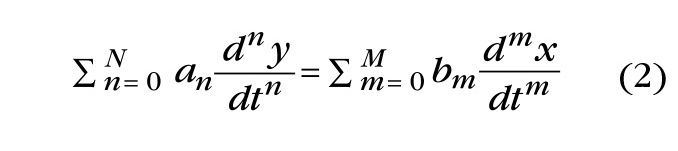
может быть представлено в следующей операторной форме:

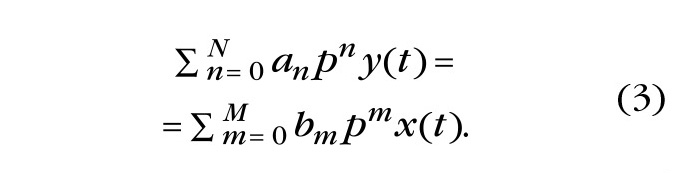
Если к суммируемым функциям уравнения (2) применить интегральное преобразование Фурье или Лапласа [4], то вместо формальных операторов p в уравнении (3), указывающих на порядок производных, появятся множители в виде степенных функций от мнимого (jω) или комплексного (s = c + jω) аргумента. С помощью этих функций легко получить два многочлена, имеющих степени N и M (N > M), которые относятся, соответственно, к левой и правой частям уравнения (2). При делении многочленов – левого на правый – получаем дробно-рациональную функцию, которую в случае преобразования Фурье принято называть частотной функцией F(jω), а в случае преобразования Лапласа – передаточной функцией W(s). Заметим, что преобразование Лапласа позволяет расширить класс функций, к которым может быть применено интегральное преобразование. Функции этого расширенного класса принято называть оригиналами по причине того, что на них накладывается математическое ограничение: они должны быть равны нулю при отрицательных значениях своих аргументов. Причину этого легко уяснить, обратив внимание на неограниченный рост экспоненты с действительным положительным показателем степени. Поэтому преобразование Лапласа в большей степени представляет интерес для изучения переходных процессов, имеющих нулевое значение до появления возмущения. Заметим, что математический смысл интегральных преобразований можно уяснить путём сопоставления их с методом замены переменной интегрирования некоторой функцией другого аргумента, который применяется в интегральном исчислении. При интегральном преобразовании осуществляется переход от исходной функции к некоторой другой (желательно более простой) с помощью подходящей дополнительной функции с двумя аргументами, вводимой под знак интеграла. При этом важно, чтобы существовало обратное преобразование. Интеграл Лапласа имеет следующий вид:

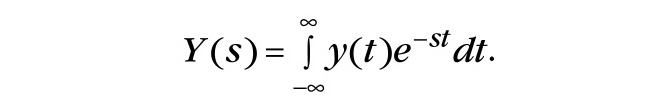
Следует заметить, что необходимо различать спектры относительных амплитуд гармоник в частотных и передаточных функциях и абсолютных величин амплитуд спектров в преобразованиях Фурье и Лапласа. Функции интегральных преобразований характеризуют спектральные плотности амплитуд гармонических составляющих воздействий на входе и соответствующих реакций на выходе систем, которые не являются реально существующими гармониками в преобразуемых функциях. Это чисто математические сущности, подобные, например, степенным или тригонометрическим функциям в соответствующих рядах. Физическая сущность возникает тогда, когда рассматриваются частотные или передаточные функции, характеризующие свойства систем. Заметим также, что решение интеграла Лапласа не представляет, говоря в общем, каких-либо существенных трудностей. Для дальнейшего изложения потребуются формулы преобразования Лапласа единичной ступенчатой функции с обычным и запаздывающим аргументами, которые имеют следующий вид:

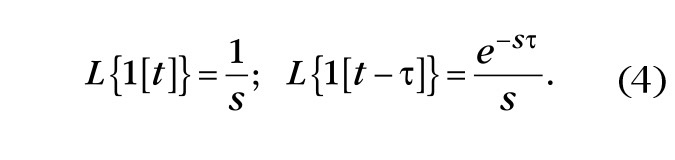
Из приведённых формул видно, что запаздыванию функции во временно¢й области соответствует умножение её изображения в частотной области на экспоненту e^–st. Отметим ещё одно свойство преобразования Лапласа. Упомянутая выше дробно-рациональная функция, получившая название передаточной функции, позволяет по известному изображению входной функции системы получить изображение выходной функции согласно выражению:

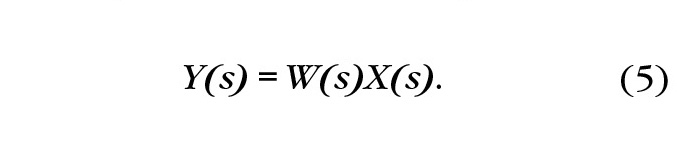
Применив в формуле (5) обратное преобразование Лапласа для функции Y(s), получим временнýю функцию (реакцию) на выходе системы.

Рассмотрим теперь другой способ решения уравнений, используемых для описания систем, который позволяет с помощью формулы интеграла свёртки получать интегральную зависимость выходной функции системы от входной функции во временно́й области. Для уяснения понятия интеграла свёртки полезно ввести в рассмотрение интегральное уравнение Вольтерры первого рода, которое имеет следующий вид:

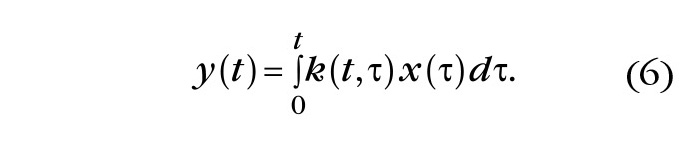
В этом уравнении искомой функцией является x(τ). Вторая функция – ядро k(t,τ), стоящая под знаком интеграла, полагается известной. Она характеризует свойства системы. Кроме того, функция в левой части равенства (6) также полагается известной. В работе Вольтерры [2] имеется замечание о том, что интегральные уравнения можно рассматривать в качестве предельного случая систем линейных обыкновенных дифференциальных уравнений. Понятно, что система таких уравнений может быть сведена к одному уравнению типа (2). В том случае, когда ядро является известной функцией запаздывающего аргумента и, кроме того, известна входная функция x(t), то из уравнения (6) выводим формулу, получившую название интеграла свёртки:

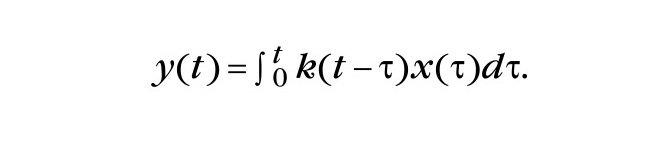
Отметим, что разностный (запаздывающий) аргумент для ядер интегральных уравнений первым ввёл в рассмот­рение, согласно работам Вольтерры [2], Н.Я. Сонин в 1880 году. Было показано, что если аргументом ядра интегрального уравнения (6) является разность (t – τ), то его решение можно получить с помощью интегрального преобразования Лапласа. В преобразованном виде решение это принимает следующий вид:

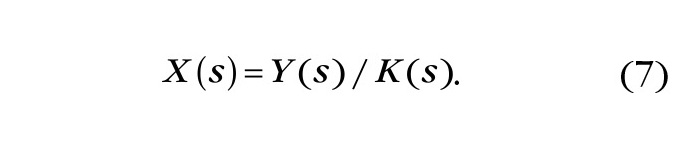
Из сопоставления формул (5) и (7) видно, что решения уравнений (2) и (6) идентичны. В дальнейшем, при детальном изучении формулы свёртки, было доказано (теорема Бореля), что преобразование Лапласа от свёртки равно произведению изображений от подынтегральных функций x(t) и k(t) при условии, что они – оригиналы. Кроме того, с помощью преобразования Лапласа были получены и другие важные результаты для теории систем типа вход–выход. Если в качестве ядра свёртки использовать переходные функции или их производные (импульсные переходные функции), то имеют место равенства, получившие название интегралов Дюамеля. Приведём одно из этих равенств, необходимое в данном случае:

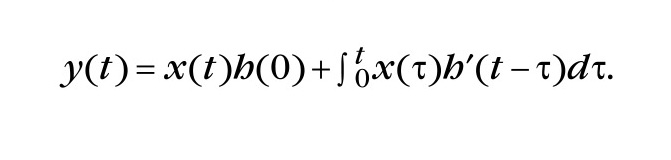
Если учесть, что h(0) = 0 и сделать подстановку h(τ)dτ=dh(τ), то формулу свёртки можно записать в следующем простом виде:

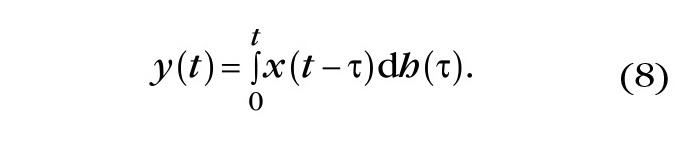
Отметим, что в подынтегральных функциях формулы (8) произведена взаимная замена аргументов на основании свойства симметрии свёртки.

Анализ структуры цифровых фильтров

Теперь, с учётом изложенных преобразований, легко сделать анализ структуры ЦФ. Очевидно, что они должны быть основаны на конечно-разностном описании систем с помощью уравнения типа (2) или формулы свёртки (8). При этом видно, что дифференциал ядра свёртки в формуле (8) будет порождать последовательность коэффициентов, равных приращениям переходной функции. Обозначая номера дискретных точек текущего непрерывного аргумента через i, номера дискретных точек запаздывающего аргумента через n и переходя с помощью численного интегрирования методом прямоугольников от интеграла свёртки к сумме линейной формы (свёрточной сумме), получаем:

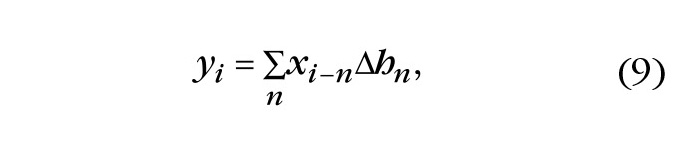
где n = 1…N.

Заметим, что индекс относится к правой границе промежутка, а число равно числу промежутков (шагов), содержащихся в интервале длительности переходного процесса h(τ). Переходные процессы, получаемые путём аналитического решения дифференциального уравнения (2), имеют бесконечную длительность. При составлении импульсной переходной функции (ИПФ) с помощью приращений переходной функции в дискретном виде будет получаться большое число коэффициентов. Однако понятно, что удаляться до бесконечности по оси абсцисс не потребуется, так как приращения будут уменьшаться, и при некоторых малых значениях их можно будет отбросить.

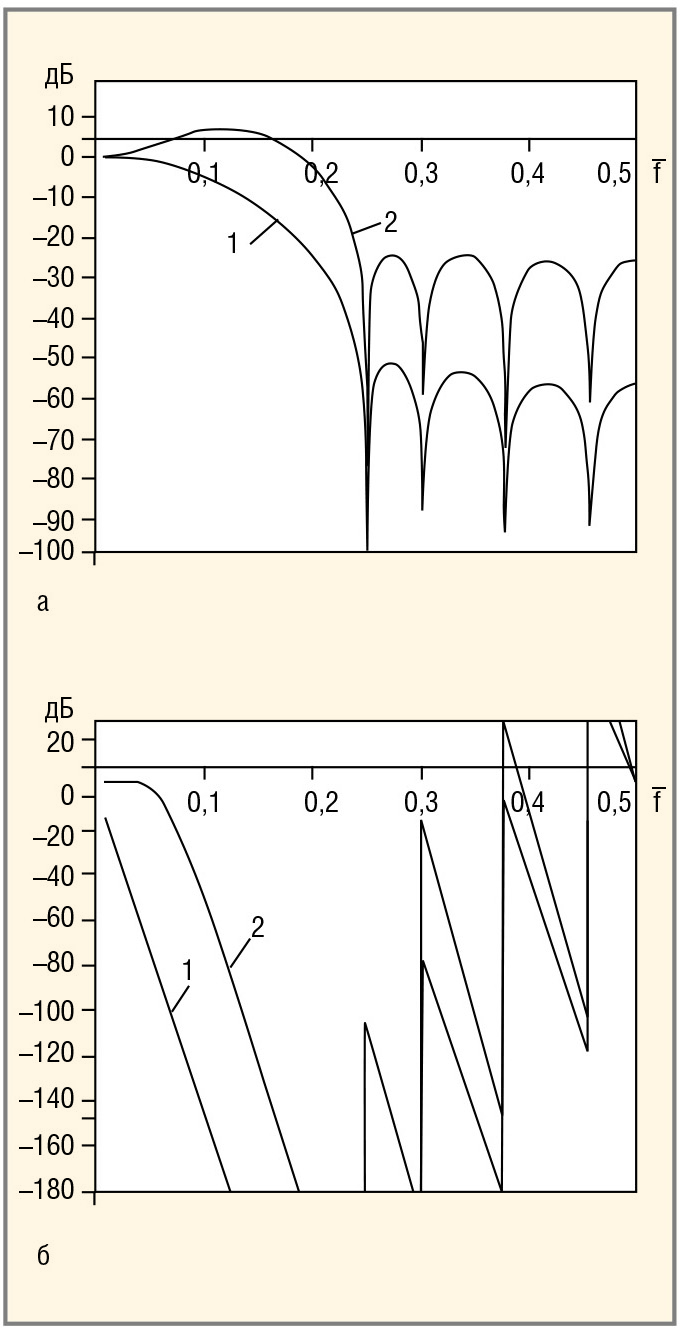
На рисунке 1а приведён пример получения коэффициентов ИПФ с помощью аналоговой переходной функции апериодического звена. Существуют два способа сокращения количества коэффициентов ИПФ. Первый из них основан на алгоритмах численного решения дифференциального уравнения (2), получаемых путём перехода к разностному уравнению. Варианты этого способа будут рассмотрены далее, а сейчас рассмотрим второй способ.

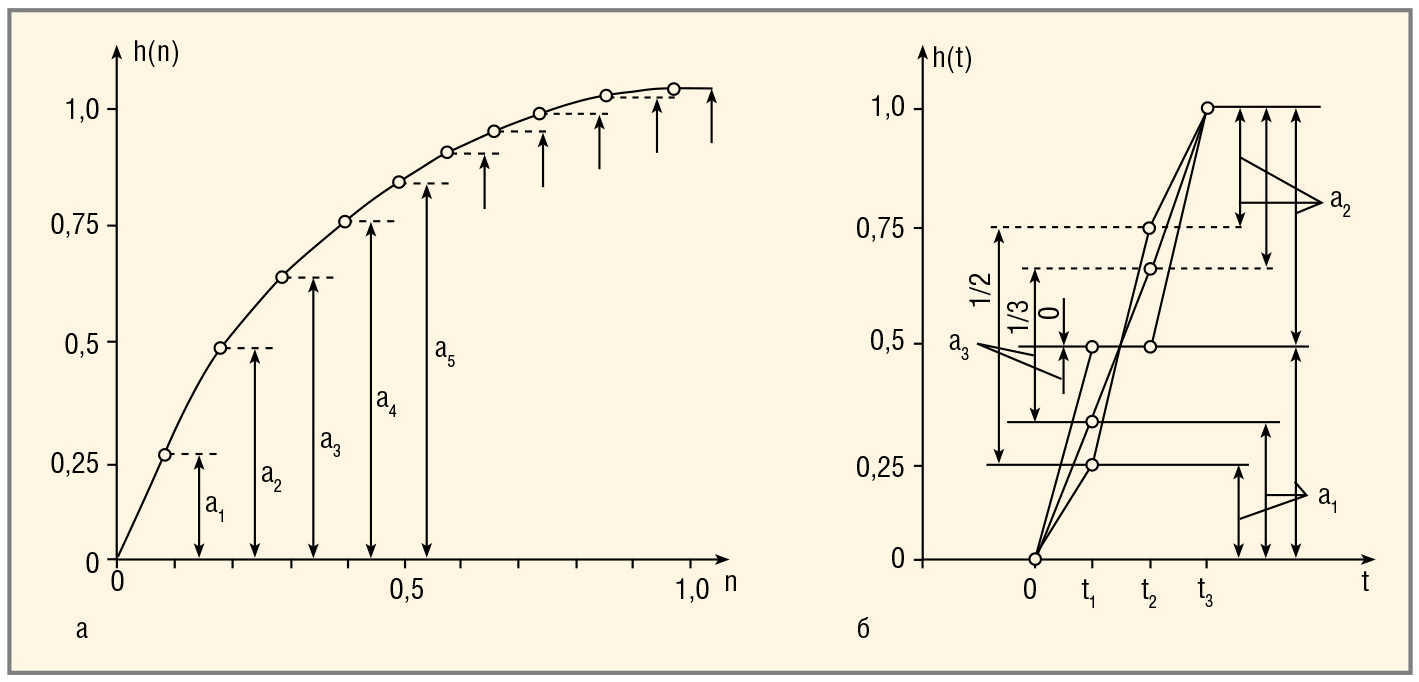
Так как ЦФ представляет собой математическую систему, переходной процесс можно искусственно сократить, сделав его в виде ломаной линии (см. рис. 1б). Одна из переходных функций представлена на рисунке в виде прямой линии, имеющей изломы только в начале и в конце переходного процесса. Она порождает ИПФ с одинаковыми значениями коэффициентов. Такой ЦФ принято называть фильтром скользящего арифметического среднего. На этом же рисунке показаны другие переходные процессы, определяющие ИПФ с разными значениями коэффициентов.

Цифровые фильтры с коэффициентами ИПФ, получаемыми путём перехода к разностному уравнению (первый способ), принято называть ЦФ с бесконечной импульсной характеристикой (БИХ), а вторым способом – с конечной импульсной характеристикой (КИХ). Далее будем различать ЦФ с чётным и нечётным числом коэффициентов, а также, что более важно, по симметричности и асимметричности значений этих коэффициентов относительно центра образованной ими последовательности.

 

Новый метод расчёта симметричных нерекурсивных ЦФ

Перейдём к описанию алгоритма предлагаемого здесь нового метода расчёта симметричных нерекурсивных ЦФ. Суть этого метода состоит в циклическом расчёте частотных характеристик ЦФ по алгоритму, составленному для каскадной формы трёхточечных ЦФ [1, 3]. Такие ЦФ использованы здесь в качестве элементарных звеньев. Существуют два вида минимально-количественных ЦФ. Один из них – чётный. Он имеет два коэффициента: {a₁, a₂}. Второй – нечётный. Он имеет три коэффициента: {a₁, a₂, a₃}. Напомним, что a_i = Δh_i = h_i – h_i–1, где i = 1…N. Минимально-количественные ЦФ важны потому, что их можно характеризовать только одним коэффициентом. Сумма всех коэффициентов ЦФ равна сумме приращений переходного процесса на единичное ступенчатое воздействие. Для двухточечных ЦФ имеем: a₁ = 1 – a₂. Для симметричных трёхточечных ЦФ имеет место равенство a₁ = a₃, поэтому они тоже однозначно определяются заданием только одного коэффициента. Например, если задать a₂, то a₁ = a₃ = (1 – a₂)/2.

Симметричные ЦФ обладают весьма важными свойствами. Например, если входная функция задана таблично, то имеется возможность исключить искажение фаз гармоник, содержащихся в её спектре. В других случаях получается линейная зависимость фазовой характеристики от частоты, аналогичная зависимости звеньев транспортного запаздывания. Величина этого запаздывания равна τ_T=Δt(N–1)/2. Отметим, что для двухточечных ЦФ существует только один вариант, при котором они могут быть симметричны, а именно: a₁ = a₂ = 0,5, из-за чего эти ЦФ используются редко. Что же касается трёхточечных ЦФ, то для них существует бесконечное множество вариантов, при которых a₁ = a₃.

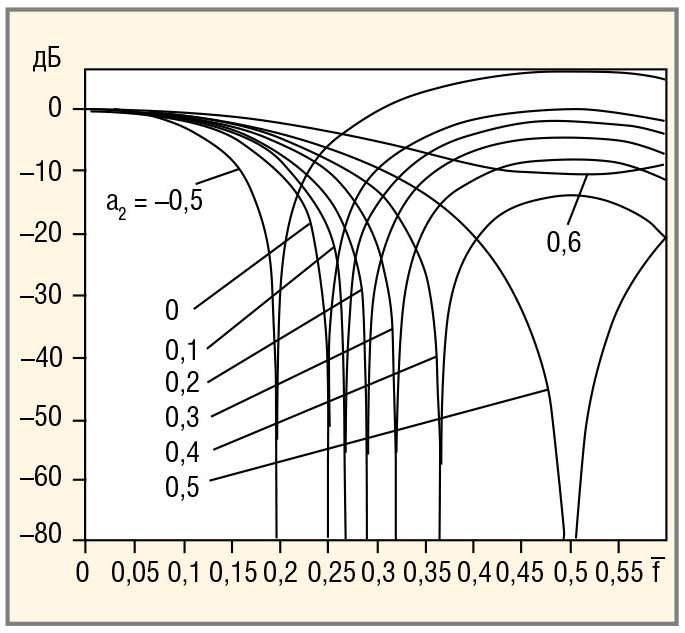
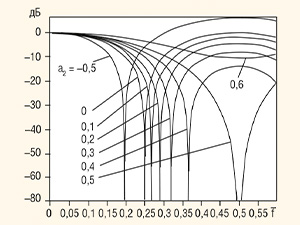
На рисунке 2 приведены логарифмические амплитудно-частотные характеристики (ЛАХ) трёхточечных симметричных ЦФ, полученные при различных значениях a₂. Острые пики ЛАХ, направленные вниз, соответствуют логарифму ординат обычных амплитудно-частотных характеристик (АЧХ) ЦФ, близких к абсциссам их нулевых значений.

Абсциссы нулей АЧХ зависят только от a₂, что видно на рисунке 2. При этом значение a₂ = 0,5 является предельным в том смысле, что при a₂ > 0,5 АЧХ вместо нуля имеет точку минимума с абсциссой, равной частоте f_max/2, где . Эта частота является границей области наложения частот. Значение ординаты ЛАХ при a₂ > 0,5 зависит от величины a₂. Гармоники, частоты которых принадлежат области наложения, дискретным способом не воспроизводятся – они как бы отсутствуют. Вместо них получаются гармоники с другими частотами, расположенными в области нижних частот (f < f_max/2), в которую они переходят по правилу симметрии относительно граничной частоты. Это правило легко уяснить, если раскрыть дискретную структуру гармоники. Заметим, что нижние частоты области наложения, диапазон значений которых равен ширине полосы заграждения ЦФ, переходят по правилу симметрии в эту полосу и там подавляются. Следовательно, в полосу пропускаемых частот ЦФ могут переходить только те гармоники из области наложения, значения частот которых превышают интервал полосы заграждения. На рисунке 2 видно, что при уменьшении a₂ ноль АЧХ трёхточечного ЦФ перемещается влево и, одновременно, происходит нежелательный подъём правой ветви ЛАХ, которая при a₂ = 0 касается оси абсцисс. Дальнейшее уменьшение a₂ в сторону отрицательных его значений приводит к усилению высоких частот полосы заграждения ЦФ. Заметим, что это обстоятельство не является препятствием для синтеза ЦФ с более широкой полосой заграждения, чем получается при a₂ = 0 (ноль АЧХ на частоте f_max/4). Левая граница полосы заграждения является величиной, задаваемой при проектировании ЦФ. Она определяется тем из входящих в каскад трёхточечным ЦФ, у которого a₂ имеет наименьшее значение по сравнению с остальными.

Выведем формулу, с помощью которой можно определить значение a₂ для заданного значения частоты. АЧХ на этой частоте должно быть равно нулю. С помощью формулы (9) запишем выражение для трёхточечного ЦФ в форме, удобной для дальнейшего анализа:

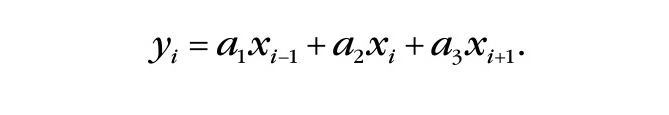
Применим к этому равенству преобразование Лапласа с учётом положительных и отрицательных (опережающих и запаздывающих) сдвигов абсцисс входной функции:

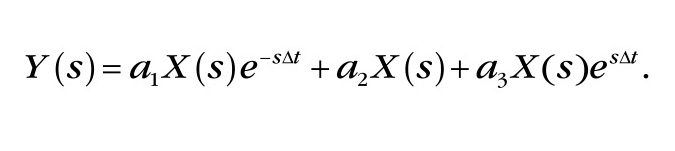
Из последнего равенства получаем передаточную функцию

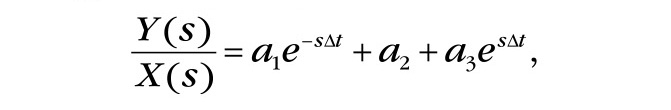
от которой переходим к частотной характеристике, полагая s = jω и используя одну из формул Эйлера для комплексных экспонент:

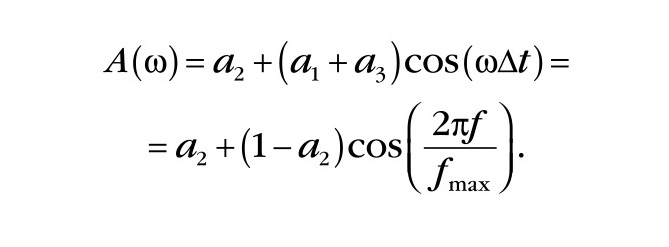
Из последнего равенства легко находим значение a₂ для случая, когда A(ω) = 0:

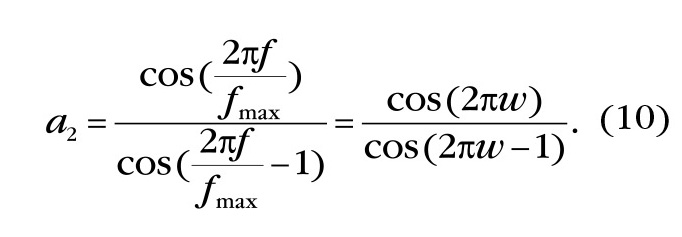
По этой формуле можно получить значение a₂ для любого значения относительной частоты f/f_max (относительную частоту обозначим через ω). Например, при ω = 0,5 (это граница области наложения частот) имеем cos (π) = –1 и поэтому a₂ = 0,5. Для другой характерной точки ω = 0,25 имеем cos(π/2) = 0 и, следовательно, a₂ = 0. С помощью формулы (10) могут быть получены значения a₂ для любых других точек ω из диапазона (0…0,5).

Упорядоченное каскадное соединение трёхточечных ЦФ

Интерес представляет непроизвольный набор точек относительных частот, в которых ординаты АЧХ равны нулю, а такое их распределение, при котором суммарная ЛАХ каскадно-соединённых трёхточечных ЦФ будет иметь в полосе заграждения последовательность гребней, максимумы которых расположены на горизонтальной прямой линии.

В качестве первого приближения к такой ЛАХ рассмотрим случай разбиения отрезка оси относительных частот в полосе заграждения ЦФ на (N – 1) частей, где N – число трёхточечных ЦФ. Отметим, что в этом случае трёхточечный ЦФ получит ноль АЧХ, совпадающий с границей наложения частот. Для увеличения степени подавления частот желательно сдвинуть его влево (внутрь полосы заграждения) так, чтобы ордината правой ветви ЛАХ этого ЦФ, абсцисса которой совпадает с границей наложения, оказалась бы на горизонтальной линии максимумов гребней. С учётом этого сдвига шаг дискретизации по частоте можно определить по формуле:

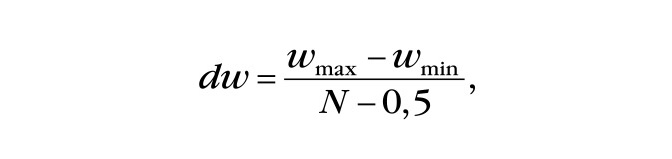
где ω_max = 0,5.

На рисунке 3а представлена ЛАХ каскада из девяти трёхточечных ЦФ, нули которой определены с помощью последовательного суммирования шагов по приведённой выше формуле: ω_i = ω_min + dω Из рисунка видно, что гребни ЛАХ расположены наклонно (отрицательный наклон).

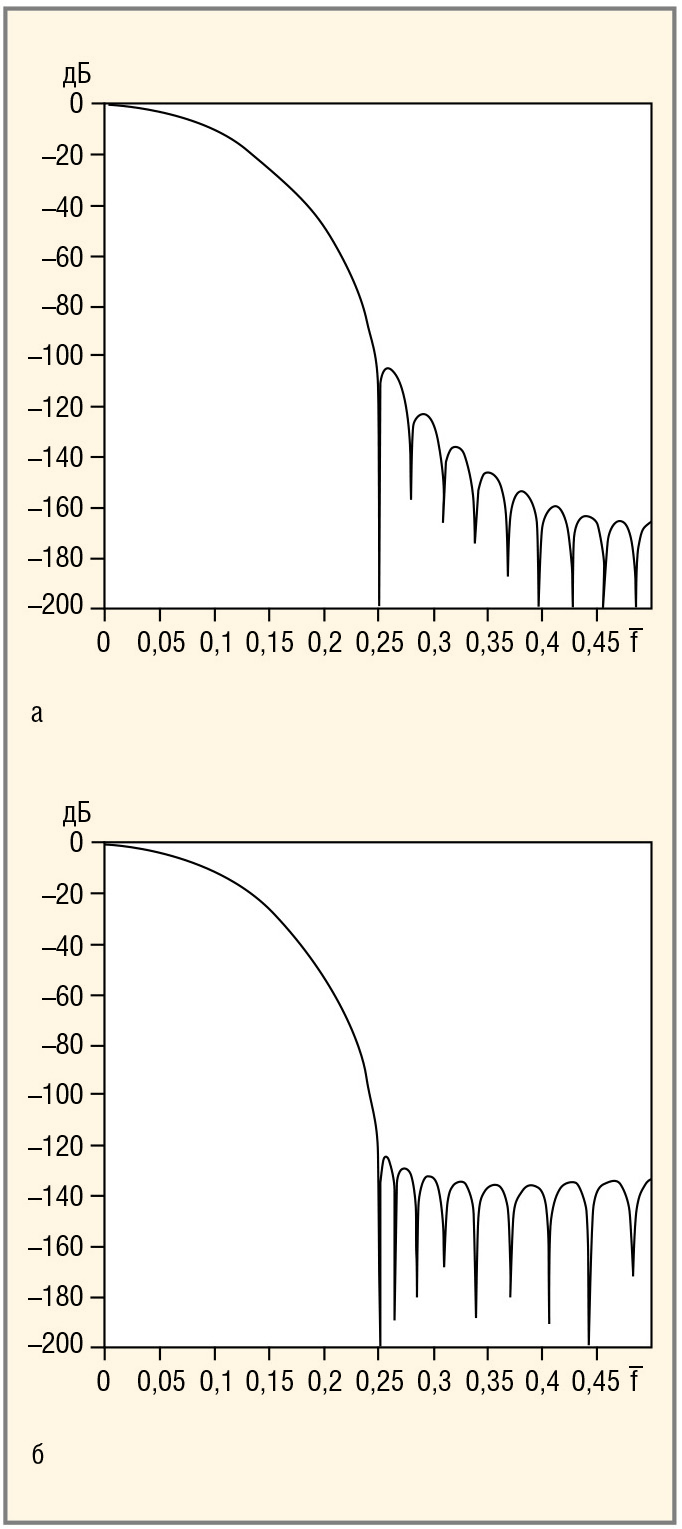
Этот «дефект» можно исправить, если воспользоваться следующей формулой разбиения оси относительных частот в полосе подавления:

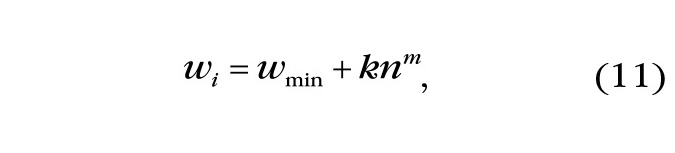
где n – порядковый номер трёхточечных ЦФ, а k – коэффициент, который вычисляется по формуле: k=(0,5-ω_min)/(N–0,5)^m. ЛАХ, представленная на рисунке 3б, рассчитана тоже для девяти коэффициентов a₂, но они получены с использованием формулы (11) при m = 1,4 (ω_min = 0,25). С помощью небольшого изменения значения m можно получить ещё более точную горизонтальность расположения гребней ЛАХ. В общем случае при проектировании ЦФ значение этого коэффициента выбирается в зависимости от ширины полосы заграждения и количества каскадов.

В листинге 1 представлен фрагмент программы расчёта ЛАХ на языке С++.

При построении алгоритма этой программы используется формула частотной характеристики трёхточечного ЦФ:

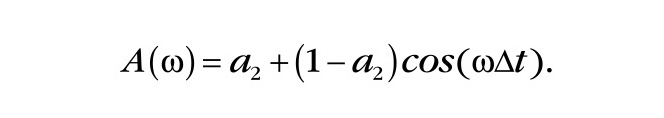
На первый взгляд, ЦФ, получаемые из трёхточечных ЦФ в каскадной форме, удобны только для расчёта частотных характеристик при проектировании, но оказываются неудобными при использовании по назначению. Поэтому возникает необходимость преобразования их к одному многоточечному ЦФ. Так как сделать это вручную, например, с помощью калькулятора, весьма трудно, а при относительно большом числе каскадов вообще невозможно, то был разработан весьма компактный алгоритм реализации процедуры сворачивания каскадной формы, фрагмент программы которой представлен в листинге 2.

Он иллюстрирует расчёт коэффициентов девятикаскадного ЦФ (для примера принято значение счётчика цикла n = 1, при котором происходит умножение пятиточечного ЦФ на трёхточечный ЦФ).

В основу алгоритма положена приведённая ниже система уравнений для вычисления коэффициентов многоточечных ЦФ. В соответствии с этой системой производится последовательное умножение получающихся результатов на очередной трёхточечный ЦФ. Результат, получающийся от умножения первых двух трёхточечных ЦФ – пятиточечный ЦФ, умножается на третий трёхточечный и так далее. Последний случай представлен в виде следующей системы равенств:

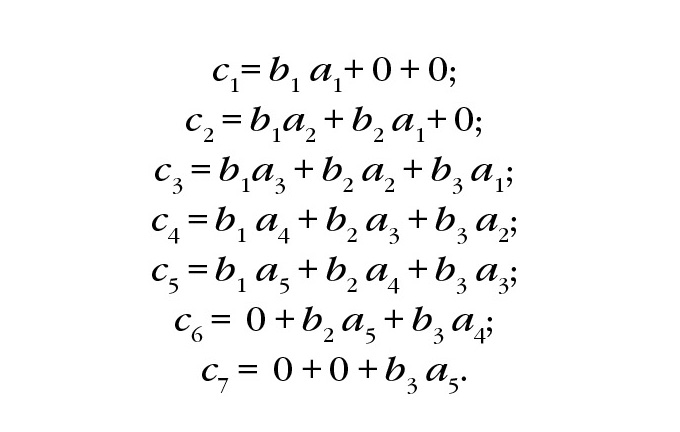
В соответствии с этой системой требуется суммировать по диагонали линейные формы, состоящие из трёх слагаемых.

После проведённых расчётов по этой программе стало видно, что при большом количестве коэффициентов многоточечных ЦФ требуется весьма высокая точность задания их значений, что можно получить только при большом числе разрядов в регистрах ЭВМ, иначе сумма всех коэффициентов будет существенно отличаться от единицы. Кроме того, возникает необходимость дополнять фильтруемую функцию нулевыми значениями за пределами начала и конца области её определения. По­этому возникла необходимость снова обратиться к каскадной форме представления ЦФ с целью разработки алгоритма и программы, свободных от указанных недостатков, но таких, чтобы в них не требовалось вводить дополнительных массивов памяти, равных массиву фильтруемой функции. Такой алгоритм оказался весьма простым; фрагмент его программы представлен в листинге 3.

Он иллюстрирует программу фильтрации табличной функции с помощью каскада из N трёхточечных ЦФ.

Порядок проектирования цифровых фильтров

При проектировании ЦФ вначале формулируются требования к желаемым характеристикам ЦФ, которыми он должен обладать. В этих требованиях указывают границу полосы пропускания частот, ширину переходной зоны, примыкающей к границе полосы задержания частот, и неравномерность частотной характеристики в пределах полос пропускания и задержания частот. Как видно на рисунках 3а и 3б, переходные зоны рассматриваемых ЦФ занимают значительную часть полосы пропускания частот. Для уменьшения этой зоны можно воспользоваться последовательно включаемыми корректирующими ЦФ, которые могут быть получены с помощью дифференцирующих звеньев двух следующих видов:

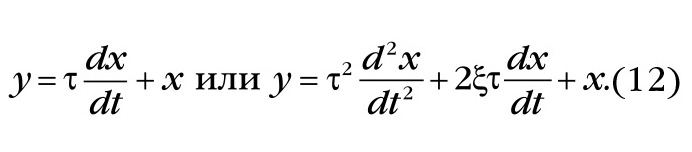
Для перехода от аналоговой формы к дискретной и получения из формулы (12) коэффициентов корректирующих ЦФ воспользуемся аппроксимацией производных входной функции с помощью конечных разностей между её отсчётами:

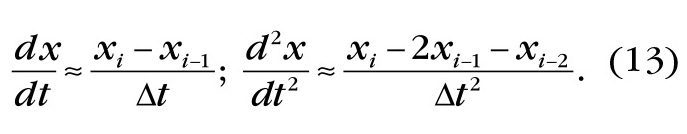
С помощью подстановки формул (13) в уравнение (12) и простых преобразований легко получить коэффициенты корректирующих ЦФ и записать формулы этих двух ЦФ в следующем виде:

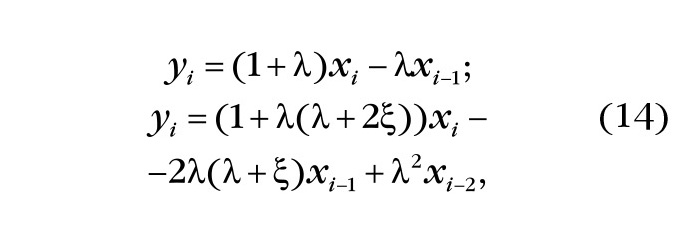
где λ=τ/Δt.

Очевидно, что корректирующие ЦФ не обладают симметрией. По­этому результирующие ЦФ также станут асимметричными. Но отсутствие симметрии нельзя в данном случае считать недостатком, так как получаем желательное уменьшение фазового сдвига.

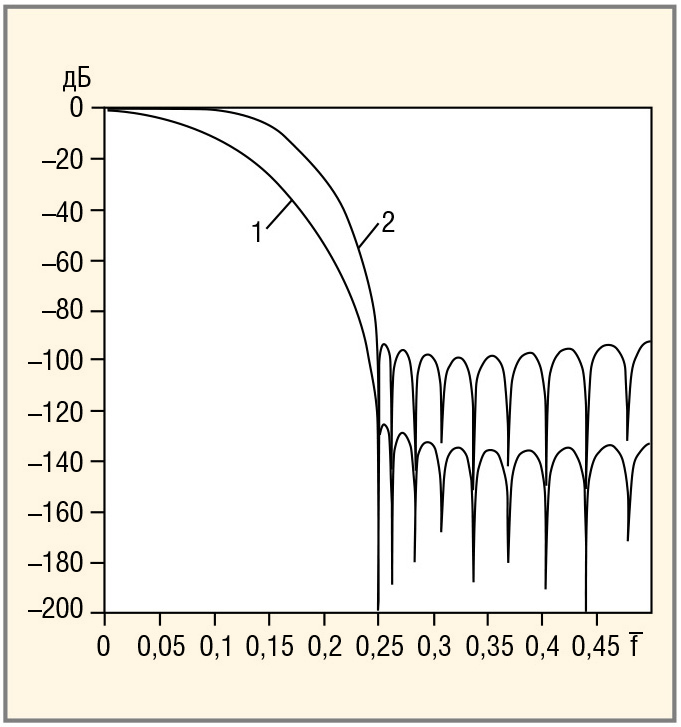
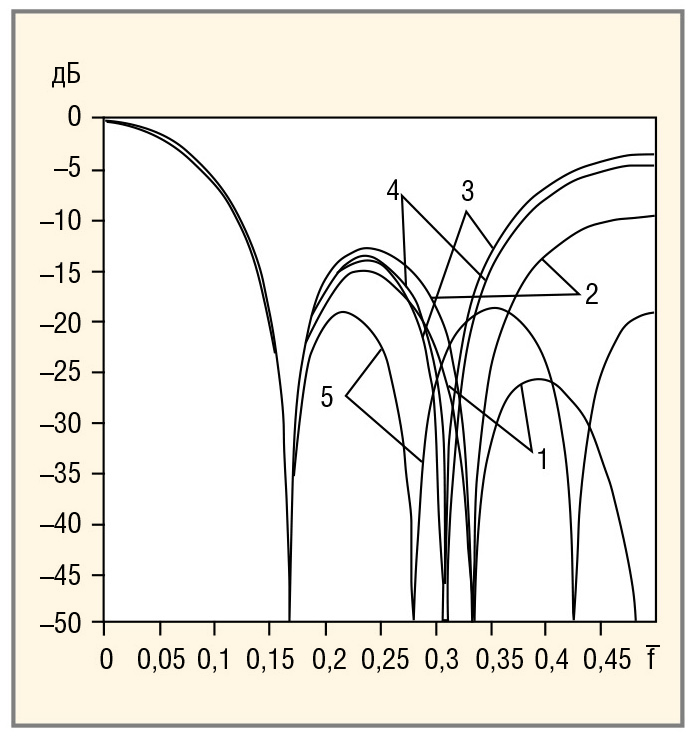
На рисунке 4 показана ЛАХ девятикаскадного ЦФ (кривая 1) и ЛАХ, которая получена путём дополнения последовательным соединением двух ЦФ типа (14) к этому девятикаскадному ЦФ (кривая 2). Видно, что в переходной зоне кривая 2 имеет большую по сравнению с кривой 1 крутизну.

Формулы (13) используются также при построении на основе уравнения (2) рекурсивных ЦФ. В этом случае уравнение (2) второго порядка примет вид:

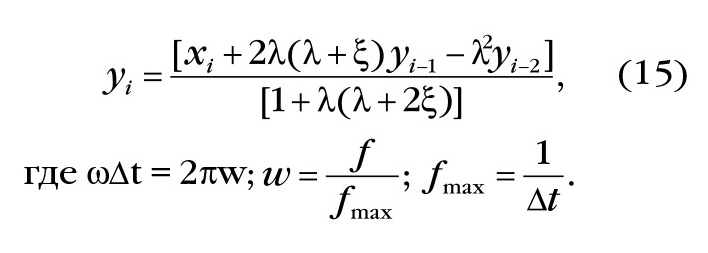
где ωΔt = 2πω; ω=f/f_max; f_max=1/Δt

Для таблично заданных функций на входе ЦФ часто оказывается удобно использовать формулы расчёта коэффициентов ЦФ, выведенные при использовании не только запаздывающих, но и опережающих (по отношению к текущему) дискретных значений функции. Для этого вместо (13) используют формулы (16) и (17):

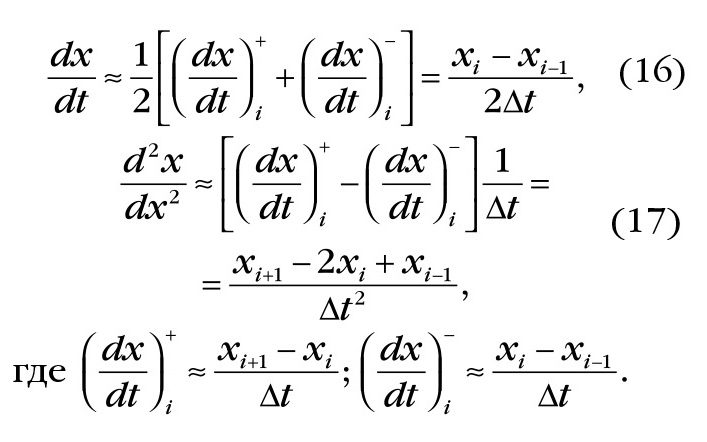
После необходимых преобразований уравнения (12) с помощью формул (15) и (16) получаем формулу (18) для ЦФ:

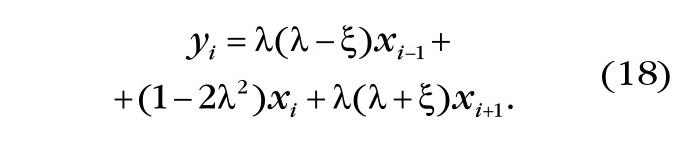
Для получения амплитудно-фазовой характеристики (АФХ) применительно к последней формуле ЦФ используют следующие простые выражения:

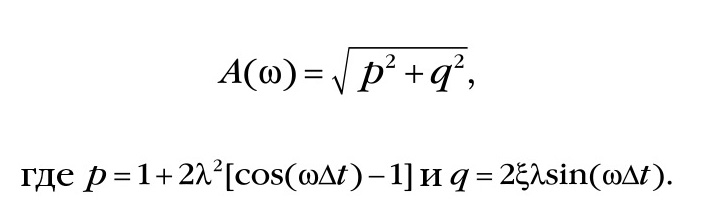
С помощью дифференцирующих ЦФ (14, 18), дополняемых к основному нерекурсивному ЦФ, можно получить в результате ЦФ, в котором отсутствует в некотором диапазоне частот сдвиг фаз гармоник. На рисунке 5 видно, что дальнейшее расширение диапазона частот, в котором отсутствует сдвиг фаз, связано с допустимостью некоторого усиления частот в полосе пропускания.

Применение ЦФ для анализа и коррекции методов численного интегрирования функций

Интересно рассмотреть ещё одну сферу применения ЦФ, связанную с анализом и коррекцией методов численного интегрирования различных (в том числе табличных) функций.

Формулы четырёх методов численного интегрирования функций – трапеций, Симпсона, Ньютона-Котеса, Уэддля и метод, обеспечивающий равномерность подавления частот в полосе заграждения (см. рис. 6, кривые 1, 2, 3, 4, 5 соответственно), преобразованные к виду ЦФ, выглядят так:

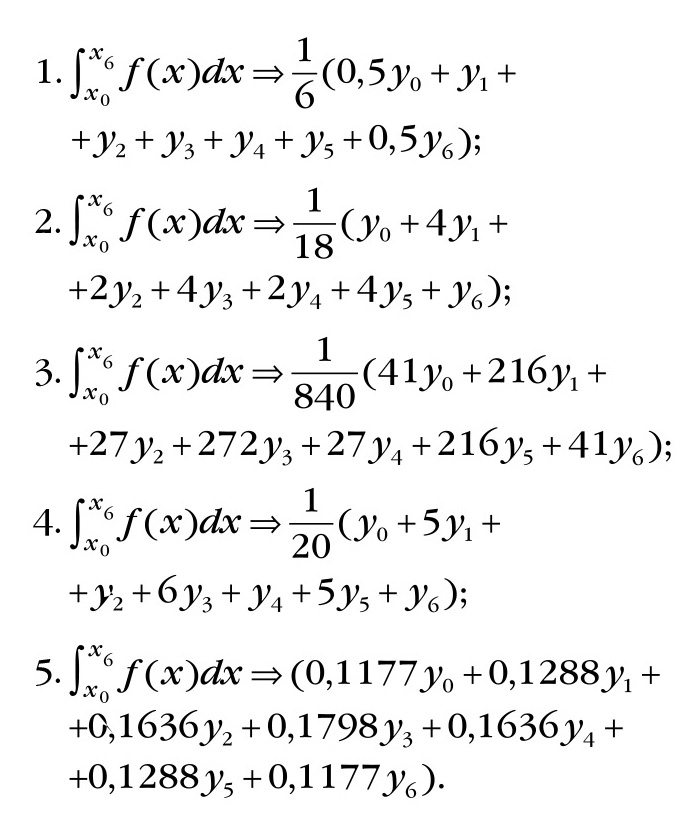
Построение методов численного интегрирования основано на аппроксимации подынтегральной функции полиномом некоторой степени, которая соответствует процессу сглаживания этой функции. ЦФ нижних частот тоже решает задачу сглаживания. Если произвести деление каждого из коэффициентов слагаемых правой части формул интегрирования на множители, стоящие перед скобками, и на сумму этих коэффициентов, то для каждого из методов получим новые коэффициенты, определяющие симметричные ЦФ.

На рисунке 6 представлены ЛАХ этих ЦФ. Видно, что только кривая 5 имеет три нуля АФХ в полосе заграждения частот. Третий ноль АФХ метода трапеций расположен на границе наложения частот. АФХ всех остальных методов вместо третьего нуля имеют минимумы, которые расположены на этой же границе (a₂ этих трёхточечных ЦФ больше 0,5). Первые нули всех АФХ – ближайшие к полосе пропускания частот – расположены на одной и той же частоте. Вторые нули АФХ оказались разделёнными на три группы. Наименьшую частоту второго нуля имеет ЦФ с равномерным подавлением частот. Рядом (правее) расположены нули АФХ методов Ньютона-Котеса и Уэддля, а ещё правее – методов Симпсона и трапеций.

Вывод

Сравнивая ЛАХ метода трапеций и метода, определяемого кривой 5, имеющих наибольшую степень подавления частот, с ЛАХ остальных методов, и используя соответствующую оценку точности в книге [4], можно прийти к выводу, что точность метода численного интегрирования определяется не степенью подавления частот. Однако оценки в источнике [4] сделаны с использованием весьма гладкой функции. Поэтому можно предположить, что при численном интегрировании быстро отклоняющихся аналитических или зашумлённых табличных функций более предпочтительными могут оказаться методы, имеющие большую степень подавления частот.

Кроме того, естественно предположить, что для подынтегральных функций, в спектре которых высокие частоты имеют существенное значение, большая точность будет получена при применении методов, имеющих более короткие интервалы интегрирования. Трансформация методов с целью перехода к коротким интервалам интегрирования наиболее легко осуществляется в методах Симпсона и трапеций, а также в методе с равномерным подавлением частот. Отметим также, что метод с равномерным подавлением частот может быть использован в роли ЦФ с узкой полосой и высокой степенью подавления частот для предварительного сглаживания интегрируемой функции, а для последующего численного интегрирования предпочтение можно отдать методу Симпсона.

Литература

1. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов. М. Связь. 1979.
2. Вольтерра В. Теория функционалов, интегральных и интегро-дифференциальных уравнений. М. Наука. 1982.
3. Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. Цифровая обработка сигналов. Справочник. М. Радио и связь. 1985.
4. Андре Анго. Математика для электро- и радиоинженеров. М. Наука. 1967.

Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!