Введение
После этапа моделирования и верификации проекта цифровой системы (схемы) наступает решающий этап проектирования – синтез логических схем в выбранной целевой технологической библиотеке. Для реализации схемы на программируемых логических интегральных схемах (ПЛИС) применяются различные пакеты программ: XST в системе проектирования ISE (Xilinx), Sinplify (Synopsys), LeonardoSpectrum [1] (Mentor Graphics).

Cинтезатор LeonardoSpectrum используется, в том числе, и для проектирования заказных СБИС. Пользователь может выполнить синтез в собственной технологической библиотеке, подготовив описания элементов целевой библиотеки, либо осуществлять управление процессом синтеза, выбирать критерии и режимы оптимизации схемы и устанавливать технологические ограничения, например требование к задержке. Программа может работать как в ОС Linux, так и в ОС Windows. На настоящий момент сменилось большое число её версий.
Для пользователей LeonardoSpectrum актуальным является вопрос о том, насколько повышается качество (уменьшается площадь, повышается быстродействие) получаемых логических схем со сменой версий программы. С этой целью в статье проанализирован опыт работы с различными версиями синтезатора LeonardoSpectrum и приведены результаты экспериментов практических примеров.
Примеры и эксперименты
Все примеры представлены в виде функциональных либо алгоритмических описаний на языке VHDL. Первую группу составляют функциональные описания комбинационной логики, соответствующие представлениям логических функций в виде систем ДНФ (двухуровневые И/ИЛИ представления) и в виде многоуровневых представлений в базисе И, ИЛИ, НЕ. Данные примеры взяты из источника [2].
Другую группу примеров составляют алгоритмические описания проектов цифровых систем, взятые из практики проектирования либо из Интернета [3] (примеры dec_8b10b, enc_8b10b). Во всех экспериментах была использована одна и та же библиотека проектирования отечественных КМОП СБИС [4], содержащая 35 элементов типа 2И-НЕ, 3И-НЕ, 2-ИЛИ-НЕ, 3-ИЛИ-НЕ (и других) и три типа триггеров.
Эксперимент 1 проводился с целью выбора критерия оптимизации (Area, Delay) и режима трудоёмкости оптимизации (Optimize effort), при которых синтез приводил к получению схем, меньших по площади и задержке. Устанавливаемый в программе параметр режима «Optimize effort» может принимать значения remap, quick, standard [5].
Смысл этих значений следующий:
- remap выполняет локальную оптимизацию и технологическое отображение в целевую библиотеку;
- quick (режим по умолчанию) выполняет одну итерацию оптимизации на основе быстрых алгоритмов и применяется на начальном этапе проектирования;
- standard выполняет несколько итераций оптимизации и технологического отображения на основе различных методов, при этом получаемые результаты, как правило, лучше, чем в режиме quick.
Синтезатором можно управлять как с помощью графического интерфейса, так и с помощью TCL-скриптов. В листинге приведён скрипт (сценарий), используемый при синтезе в эксперименте 1, строка комментариев начинается с символа #. При проведении эксперимента 1 в скрипте вместо параметра area команды optimize использовался параметр delay, а вместо значения standard параметра effort использовались также значения remap либо quick.
По результатам сравнения синтезированных проектов схем версии программы LeonardoSpectrum можно условно поделить на три группы – L2003, L2006 и L2011, дающие примерно одинаковые результаты синтеза. Основанием для такого деления являются существенные различия в площади и задержке получаемых логических схем (см. табл. 1).
Результаты первого эксперимента по сравнению трёх базовых версий L2003, L2006, L2011 приведены в таблице 2, где знаком «*» отмечены лучшие результаты – параметры площади (в условных единицах) и задержки (в наносекундах) отдельно для каждой из версий. Жирным шрифтом выделены лучшие решения совместно по трём версиям синтезатора. В столбце «Критерий оптимизации» приведён критерий Area или Delay, в столбце «Трудоёмкость оптимизации» указано значение этого параметра, при котором получена схема меньшей площади либо с меньшей задержкой.
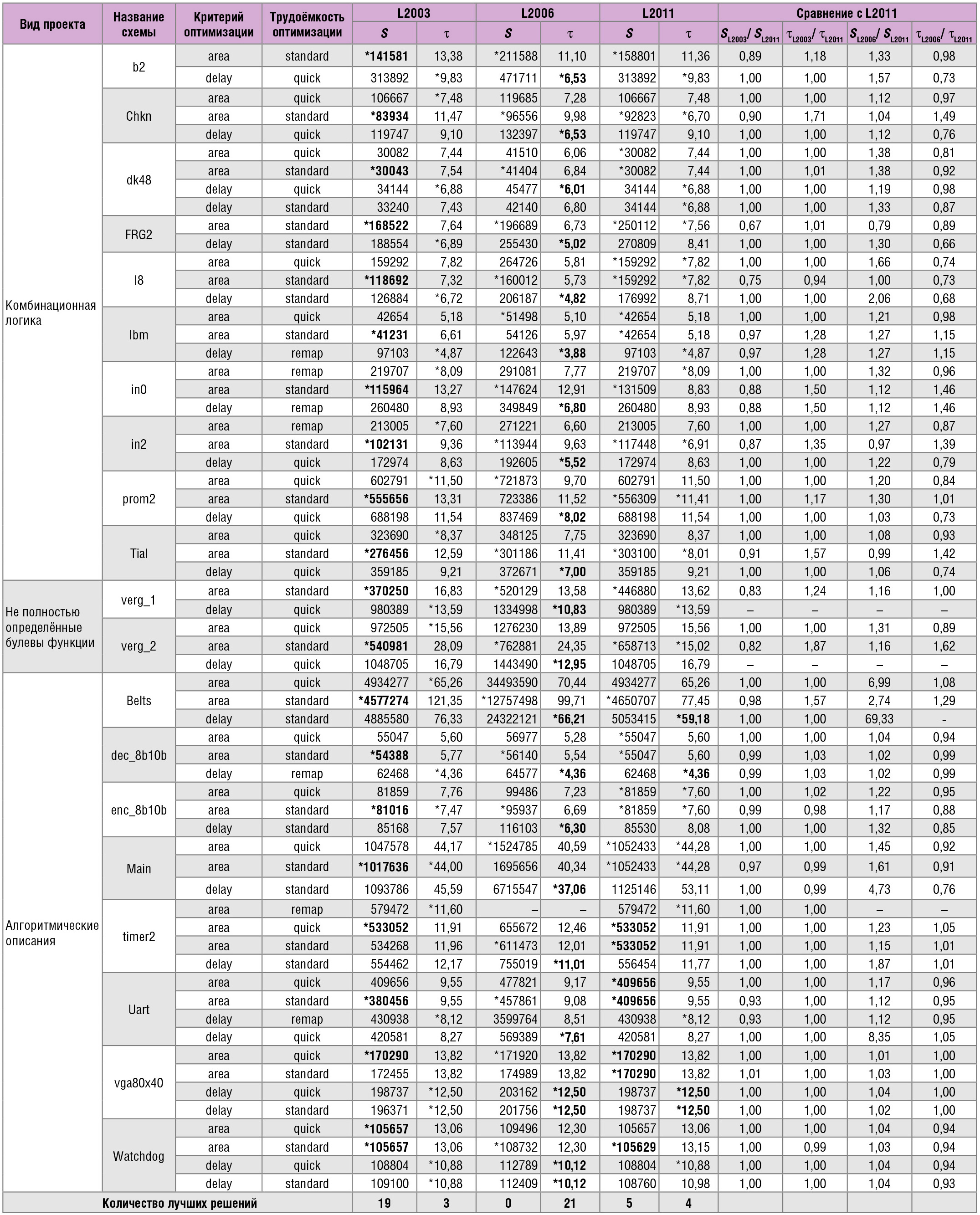
Проанализировав таблицу 2, можно сделать следующие выводы. Для версии L2006 выбор критерия оптимизации Area приводил к схеме меньшей площади, а выбор критерия Delay – к схеме с меньшей задержкой. Например, для первого примера b2 выбор режима <Area, Standard> позволил реализовать схему с площадью SL2006 = 211588 и задержкой τL2006 = 11,10 (см. первую строку таблицы 2). В режиме <Delay, Quick> результат уже другой: SL2006 = 471711 и τL2006 = 6,53 (см. вторую строку таблицы 2). Звёздочкой в первой и второй строках отмечены меньшие значения площади и задержки. Для этого примера выбор режимов <Delay, Standard>, <Delay, Remap> и др. приводит к схемам с большей задержкой. Однако лучшее (по площади) решение для примера b2 обеспечила версия L2003, поэтому значение SL2003 = 141581 отмечено звёздочкой и выделено жирным шрифтом для трёх версий. Наименьшее значение задержки для данной схемы обеспечила версия L2006, поэтому значение τL2006 = 6,53 выделено жирным шрифтом для трёх версий.
Для версий программы L2003, L2006 и L2011 критерий оптимизации Auto приводил к тем же результатам, что критерий Area, поэтому критерий Auto далее не упоминается.
Таким образом, версия L2003 позволяет получать схемы наименьшей площади при тех же режимах синтеза, что в версиях L2006 и L2011. Версия L2006 реализует схемы с наименьшей задержкой. Сравнения версий LeonardoSpectrum приведены на диаграммах: площади схем показаны на рисунке 1, задержки – на рисунке 2.
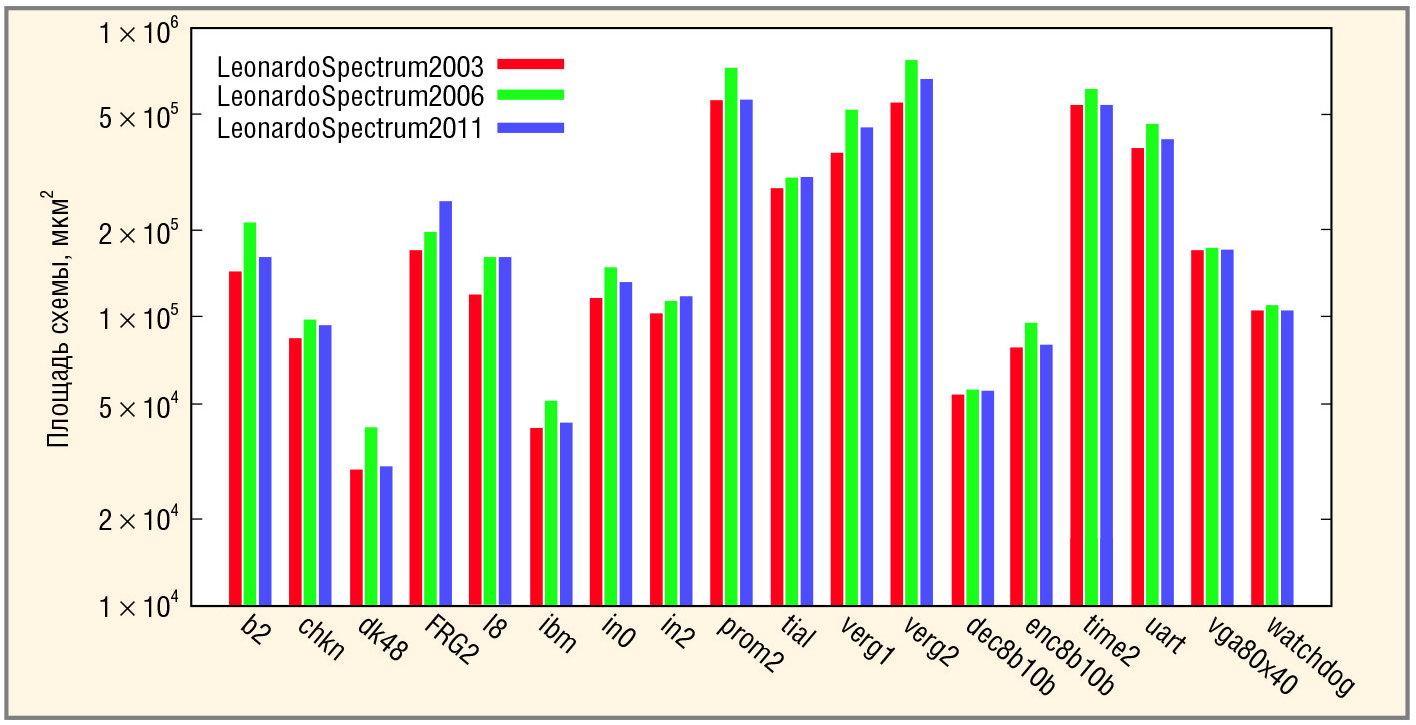
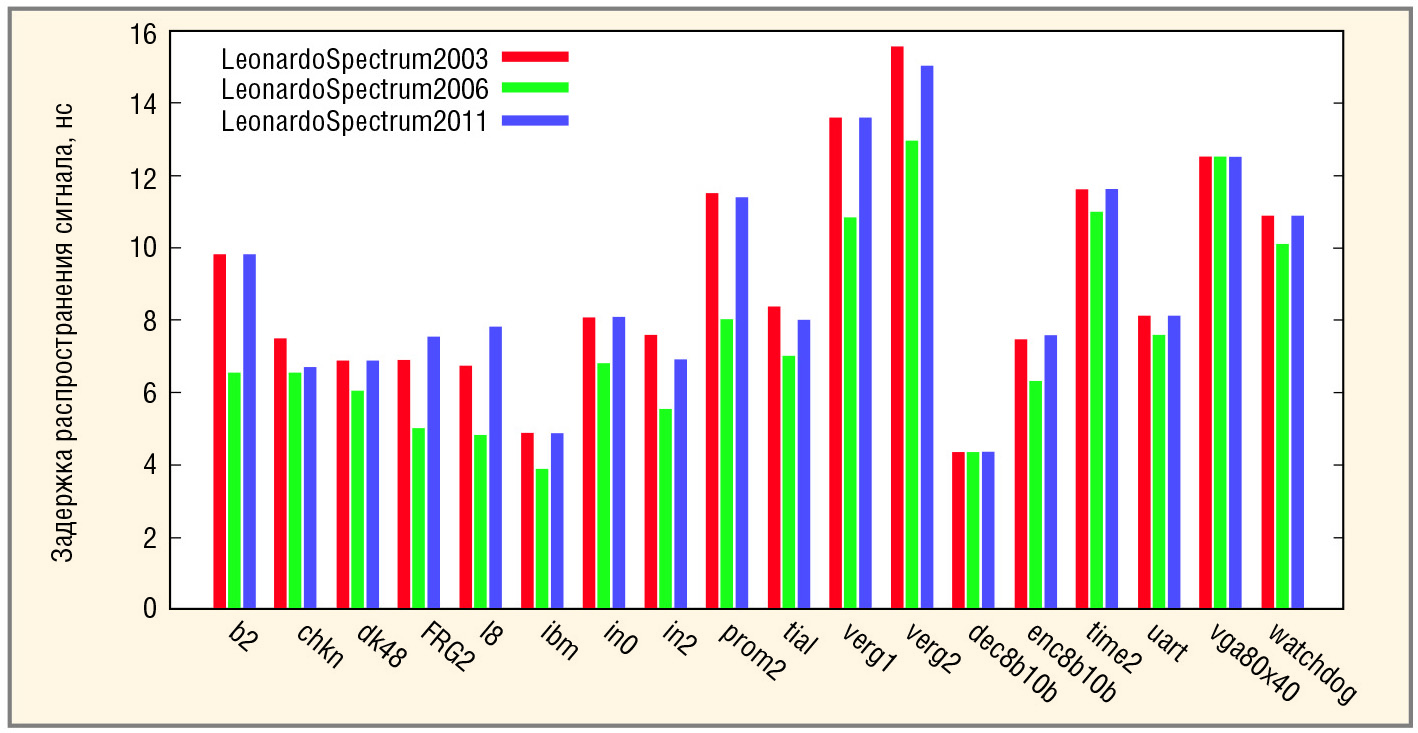
Видно, что версия L2011 позволяет получать компромиссные схемы. Если же требуется реализовать схему с меньшей задержкой, то следует воспользоваться версией L2006, понимая при этом, что проигрыш по площади может быть весьма значительным.
Вернёмся к первому примеру b2 (см. табл. 2). Здесь версия L2006 позволяет уменьшить задержку до τL2006 = 6,53 нс и получить площадь SL2006 = 471711, версия L2011 позволяет уменьшить площадь до SL2011 = 158801 и получить задержку τL2011 = 11,36 нс.
Эксперимент 2 проводился с целью изучения эффективности повторного синтеза для уменьшения задержки схемы. Для этого в скрипт (см. листинг) перед командой optimize добавлена команда set input2output 7.73, устанавливающая требуемое значение задержки (т.е. 7,73 нс). Каждый раз оно устанавливалось на 10% меньше достигнутого, и синтез выполнялся снова. Однако на втором либо третьем проходе, как правило, уменьшение задержки не происходило, а увеличивалась площадь схемы.
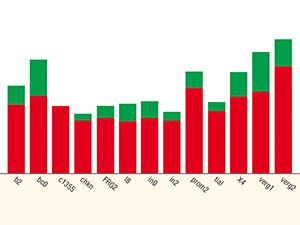
Пользователь может устанавливать требуемое значение задержки, но программа часто синтезирует схему, задержка которой лишь приближена к желаемому значению. Для примера b2 площадь SL2011 = 313892, а задержка схемы составляет τL2011 = 9,83 нс. Требование уменьшения задержки до τ = 6,16 нс привело к синтезу схемы с площадью SL2011 = 414399 и задержкой τL2011 = 7,70 нс. Таким образом, уменьшение задержки схемы на 27% увеличило её площадь на 25%. На рисунке 3 показана диаграмма уменьшения задержек схем в эксперименте 2 для версии L2011 (зелёным цветом отмечено относительное уменьшение задержки).
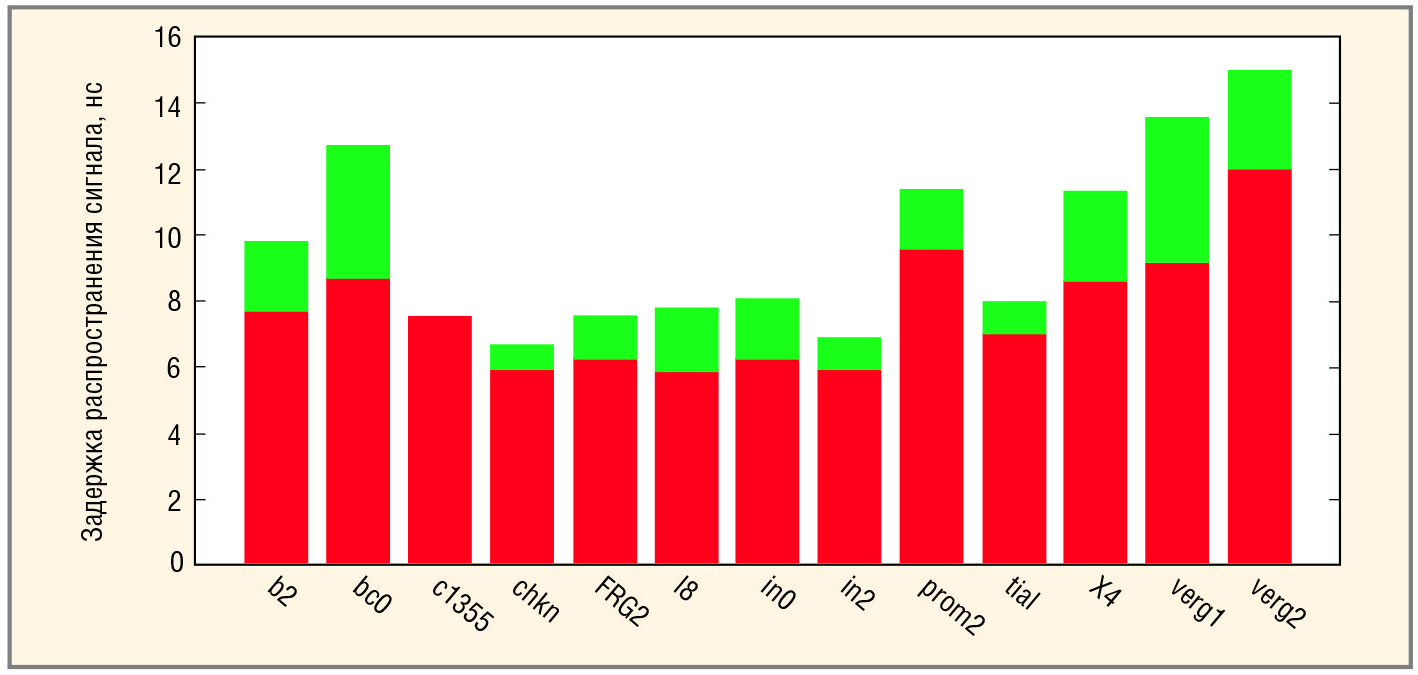
Таким образом, после последовательного выполнения двух требований уменьшения задержки получаемой схемы на 10%, задержка исходной схемы снижалась примерно на 18%, при этом минимальное уменьшение задержки составляло 2%, а максимальное – 40%.
Следует отметить, что требование получения схемы с малой задержкой при проектировании в целевой библиотеке заказных СБИС часто вообще не может быть выполнено – схемные реализации с требуемыми характеристиками задержек просто не существуют, поэтому никакие ухищрения и варьирование параметров синтеза не помогают.
Эксперимент 3 был посвящён сравнению двух форм представления систем логических функций: дизъюнктивных нормальных форм (ДНФ) и бинарных диаграмм решений (Binary Decision Diagram, BDD) [6]. На потоке из 62 практических примеров было установлено, что наиболее эффективной формой представления систем функций при синтезе схем из библиотечных элементов являются логические уравнения, соответствующие представлениям систем функций в виде BDD.
Диаграммы решений строятся на основе разложения Шеннона. Разложением Шеннона полностью определённой булевой (логической) функции f (x1,..., xn) по переменной xi называется представление f (x1,..., xn) в виде:
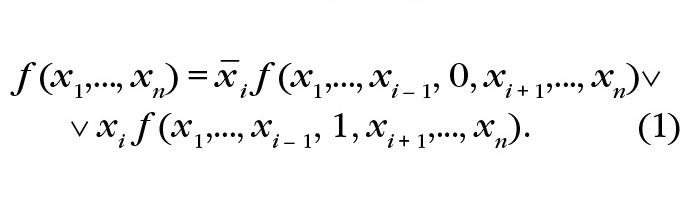
Функции f (x1,..., xi – 1, 0, xi + 1,..., xn) и f (x1,..., xi – 1, 1, xi + 1,..., xn) в (1) являются коэффициентами разложения, они получаются из функции f (x1,..., xn) подстановкой вместо переменной xi константы 0 или 1, соответственно. Диаграмма задаёт в виде графа последовательность разложений Шеннона исходной функции и получаемых коэффициентов разложения. Минимизация сложности BDD основана на том, что в процессе разложения системы функций могут появляться одинаковые коэффициенты разложения не только у одной, но и у нескольких (либо даже у всех) функций, входящих в систему. Выделение одинаковых подфункций (коэффициентов разложения) приводит к сокращению аппаратной сложности и, соответственно, площади схемы. Минимизация BDD осуществлялась с помощью программы TIE_BDD [7].
Приведём пример многоуровневого разложения, соответствующего BDD. Обозначим через <x1, x2, x3, x4, x5, x6> первую из n! перестановок переменных, по которой проведём разложение Шеннона для системы ДНФ функций:
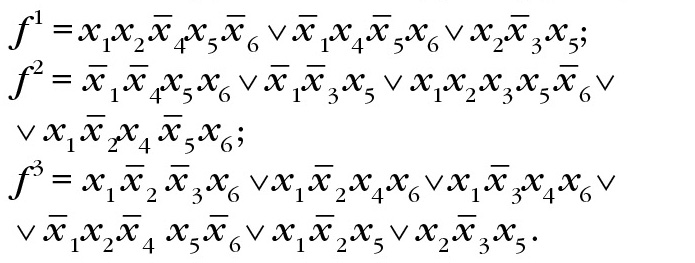
Построенные для данной системы функций коэффициенты разложения Шеннона дают следующее многоуровневое представление системы функций:
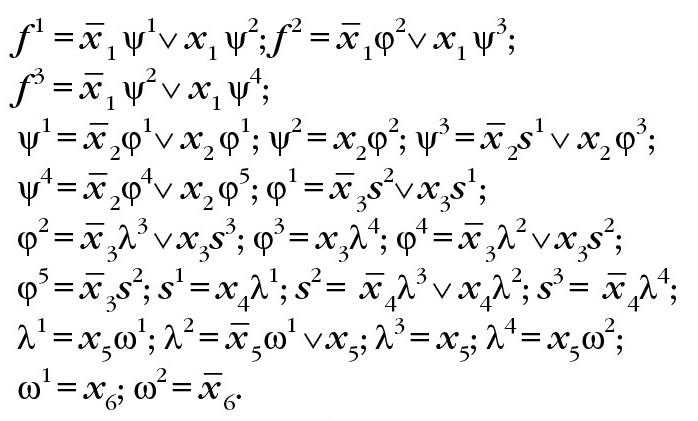
Основной проблемой при построении многоуровневых представлений меньшей сложности является выбор перестановки переменных, которая приводит к возможно меньшему числу логических выражений приведённого выше вида. В экспериментах программа TIE_BDD строила BDD по 5000 случайно выбираемым перестановкам переменных и выбирала из рассмотренных вариантов диаграммы наименьшей сложности.
Эксперименты на практических примерах [2] комбинационных схем показали, что в подавляющем большинстве случаев (41 пример из 62) использование многоуровневых представлений вместо ДНФ позволяло синтезировать в версии L2011 схемы меньшей площади, чем по исходным описаниям функций, соответствующих ДНФ. Напомним, что при синтезе функциональные описания комбинационных схем в виде ДНФ и в виде разложений Шеннона были представлены на языке VHDL. Некоторая информация об алгоритмах оптимизации, применяемых синтезатором LeonardoSpectrum, содержится в [5, с. 122]. Таким образом, судя по результатам эксперимента 3, комбинационные схемы в библиотечном базисе лучше синтезировать по минимизированным BDD, а не по минимизированным системам ДНФ, представляющим логические функции.
Возможность уменьшения площади комбинационных схем имеется и при повторном синтезе описания, полученного с помощью команды unmap. Такие эксперименты с повторным синтезом, выполнением команды unmap и сменой целевых библиотек синтеза описаны в [8]. Стили кодирования (Encoding Style) не имеют значения для комбинационной логики, однако для схем с триггерами они позволяют варьировать параметры площади и быстродействия. С другими управляющими параметрами синтеза LeonardoSpectrum можно ознакомиться в [1].
Выводы
На испытанном потоке проектов схем наилучшие решения по площади давала версия L2003, по задержке – версия L2006. Новые версии программы L2011 ориентированы на уменьшение площади схем, при этом задержки, естественно, увеличиваются. В версиях L2003 и L2006 установка критерия оптимизации «Delay» приводила к схемам с минимальной задержкой, однако для более поздних версий L2011 установка критерия «Delay» практически не влияла на получение схемы с меньшей задержкой; минимум задержки приходился на другие режимы, в основном, <Area, Standard>.
При общем совершенствовании программы LeonardoSpectrum в старых версиях синтезатора можно реализовать лучшие решения. Поэтому в ответственных случаях целесообразно выполнять синтез как в новых, так и в старых версиях программы, и выбирать лучшие решения по тому или иному критерию.
Литература
- Бибило П.Н. Системы проектирования интегральных схем на основе языка VHDL. StateCAD, ModelSim, LeonardoSpectrum. СОЛОН-Пресс. 2005.
- http://www1.cs.columbia.edu/~cs4861/sis/espresso-examples/ex.
- http://opencores.org/project,8b10b_encdec,overview.
- Бибило П.Н., Кириенко Н.А. Оценка энергопотребления логических КМОП-схем по их переключательной активности. Микроэлектроника. № 1. 2012. С. 65–77.
- LeonardoSpectrum User’s Manual, Software Release 2011a. May 2011.
- Кнут Д.Э. Искусство программирования. Том 4. А. Комбинаторные алгоритмы. Часть 1. ИД Вильямс. 2013.
- Бибило П.Н., Леончик П.В. Алгоритм построения диаграммы двоичного выбора для системы полностью определённых булевых функций. Управляющие системы и машины. № 6. 2009. С. 42–49.
- Бибило П.Н., Романов В.И. Логическое проектирование дискретных устройств с использованием продукционно-фреймовой модели представления знаний. Ленанд. 2014.
Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!