Основы измерения коэффициента шума в радиочастотном и микроволновом диапазонах. Часть 1

Современным радиоприёмным сис­темам зачастую приходится работать с очень слабыми сигналами. При этом слабые сигналы маскируются шумами, вносимыми компонентами системы. Способность системы обрабатывать сигналы низкого уровня характеризуется такими параметрами, как чувствительность, коэффициент битовых ошибок (BER) и коэффициент шума. Коэффициент шума – особенный параметр, поскольку он применим не только к системе в целом, но и к её компонентам: предусилителю, смесителю, усилителю ПЧ. Регулируя коэффициент шума и коэффициент передачи компонентов системы, разработчик тем самым регулирует коэффициент шума всей системы. Если коэффициент шума известен, то, зная ширину полосы, легко оценить чувствительность системы. Коэффициент шума часто выступает ключевым параметром, отличающим одну систему от другой, один усилитель от другого, один транзистор от другого. Поскольку характеристика «коэффициент шума» играет столь важную роль, измерять её с высокой точностью и надёжностью необходимо как поставщикам изделий, так и заказчикам.

Для получения высокоточных и понятных результатов измерения без выполнения сложных ручных процедур существуют приборы для измерения коэффициента шума с простым пользовательским интерфейсом. Их использование не требует глубоких знаний в области теории шума. Однако некоторая базовая подготовка будет полезной, поскольку позволит правильно интерпретировать результаты и составить целостную картину действия шумов в радиочастотных и микроволновых системах.

Значение шума в системах связи

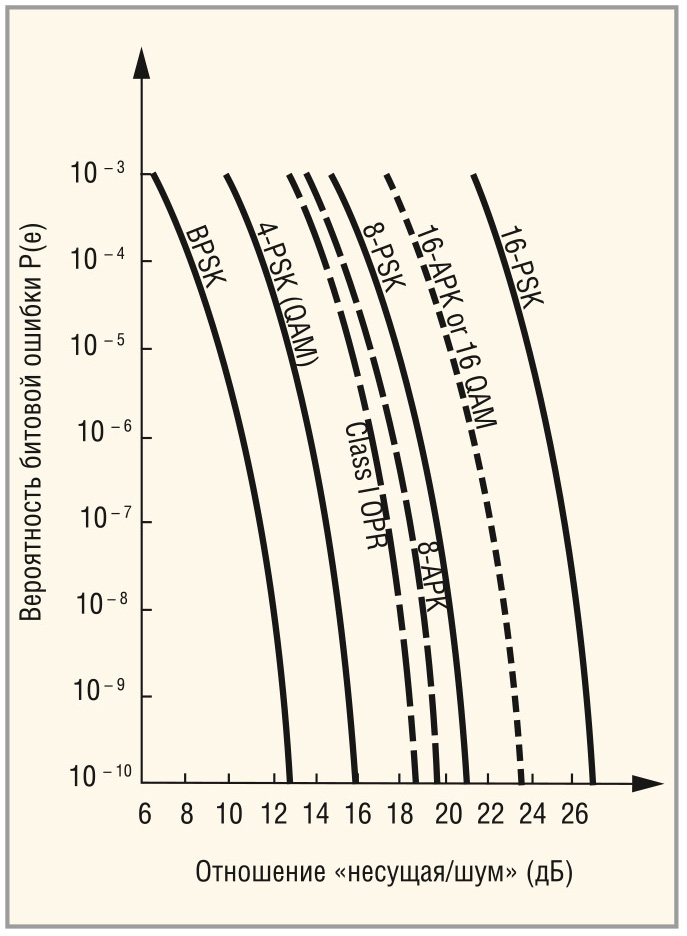
В системах связи отношение сигнал/шум (S/N) на выходе приёмной системы является очень важным параметром. С трудностями прослушивания и распознавания радиосигналов в присутствии шумов многие знакомы не понаслышке. Однако способность к распознаванию аудиоинформации сложно оценить количественно, поскольку она во многом зависит от человеческого фактора – знания языка, степени усталости, натренированности, опыта, а также от содержания сообщения. Коэффициент шума и чувствительность, напротив, могут получить объективную количественную оценку. Эти два параметра тесно связаны. Для цифровых систем связи в качестве количественной меры надёжности часто используется коэффициент битовых ошибок (BER) или вероятность появления битовой ошибки P(e). Коэффициент битовых ошибок связан с коэффициентом шума нелинейно. Так, при постепенном уменьшении отношения сигнал/шум значение BER резко возрастает вблизи уровня шума, где последовательность единиц и нулей начинает сбиваться. Коэффициент шума характеризует степень работоспособности системы, тогда как BER показывает, является ли система действующей. На рисунке 1 показана зависимость вероятности ошибки от отношения несущая/шум (которое может интерпретироваться как отношение сигнал/шум) для нескольких видов цифровой модуляции. Видно, что при изменении отношения сигнал/шум всего на несколько децибел BER изменяется на несколько порядков.

Отношение сигнал/шум на выходе устройства зависит от отношения сигнал/шум на входе и коэффициента шума данного устройства. При этом в наземных системах отношение сигнал/шум на входе зависит от мощности передатчика, коэффициента усиления передающей антенны, коэффициента передачи атмосферы, температуры атмосферы, коэффициента усиления приёмной антенны и коэффициента шума приёмника. Снижение коэффициента шума приёмника оказывает такое же влияние на отношение сигнал/шум на выходе, как и улучшение любого другого параметра.

Источники шума

Измеряемый шум является результатом спонтанных изменений в обычных процессах, протекающих в электрическом оборудовании.

Тепловой шум рождается в результате колебаний электронной и дырочной проводимости из-за конечной температуры. Спектр некоторых колебаний лежит в измеряемой полосе частот, и эти колебания вносят шум в полезные сигналы. Спектр теплового шума в полосах радиочастотного и микроволнового диапазонов приблизительно одинаков. Мощность теплового шума при согласованной нагрузке равна kTB ×Вт, где k – постоянная Больц­мана (1,38 × 10^–23 Дж/К), T – температура в кельвинах, B – шумовая полоса системы.

Дробовый шум порождается дискретной природой протекающего тока. Другие случайные явления, связанные с дискретной природой материи, также вызывают шум, подобный дробовому. Примерами таких явлений могут быть генерация и рекомбинация пар дырка/электрон в полупроводниках (G-R шум) и разделение эмиттерного тока между базой и коллектором в транзисторах (шум декомпозиции). Характеристики этих шумов подобны характеристикам тепловых шумов, их частотный спектр в основном постоянен и спектральная плотность мощности шумов по всем радиочастотным и микроволновым диапазонам одинакова.

В электрических устройствах случайные шумы имеют множество причин. При определении характеристик шума обычно ссылаются на комбинацию различных причин, влияющих на компонент. Комбинированный эффект зачастую рассматривается так, как если бы он был вызван тепловым шумом. Когда говорят, что устройство имеет определённую шумовую температуру, это не означает, что такова физическая температура компонентов. Просто мощность шума эквивалентна мощности теплового источника шума. Хотя шумовая температура прямо не связана с физической температурой, такая зависимость может существовать. Иногда можно достичь очень низкого коэффициента шума, охладив устройство ниже температуры окружающей среды.

В данной статье не рассматривается влияние человеческого фактора, хотя при приёме слабых сигналов оно может быть значительным. Проблемы шумов, вызываемых системами зажигания, искровыми разрядами, нежелательным приёмом побочных сигналов, а также электромагнитными возмущениями в атмосфере, обычно решаются техническими средствами – изменением местоположения устройства, фильтрацией и надлежащим экранированием.

Понятие коэффициента шума

Наиболее обоснованное определение коэффициента шума вошло в употреб­ление в 1940 г. с подачи Гарольда Фрииса, который определил коэффициент шума цепи (F) как отношение показателя сигнал/шум на входе к показателю сигнал/шум на выходе.

Таким образом, коэффициент шу­ма цепи отражает степень ухудше­ния отношения сигнал/шум при прохождении сигнала через цепь. Идеальный усилитель усиливал бы шум на входе вместе с сигналом, поддерживая равные значения пока­зателей сигнал/шум на входе и на выходе (источником шума на входе часто является тепловой шум, обус­ловленный температурой земной по­верхности или потерями в системе). Однако реальный усилитель вносит некоторый дополнительный шум от собственных компонентов и ухудшает отношение сигнал/шум. Цепь с низким коэффициентом шума себя оправдывает.

Понятие коэффициента шума применимо только к цепям (по крайней мере, с одним входным и одним выходным портом), где происходит обработка сигнала. В данной статье рассматриваются в основном двухпортовые цепи. Смесители, как правило, являются трёхпортовыми устройствами. Однако они обычно рассматриваются как двухпортовые с гетеродином, подключённым к третьему порту.

Коэффициент шума не зависит от коэффициента передачи. Когда шум накладывается на сигнал, то в дальнейшем усилению подвергаются как сигнал, так и шум. Следовательно, отношение сигнал/шум не меняется.

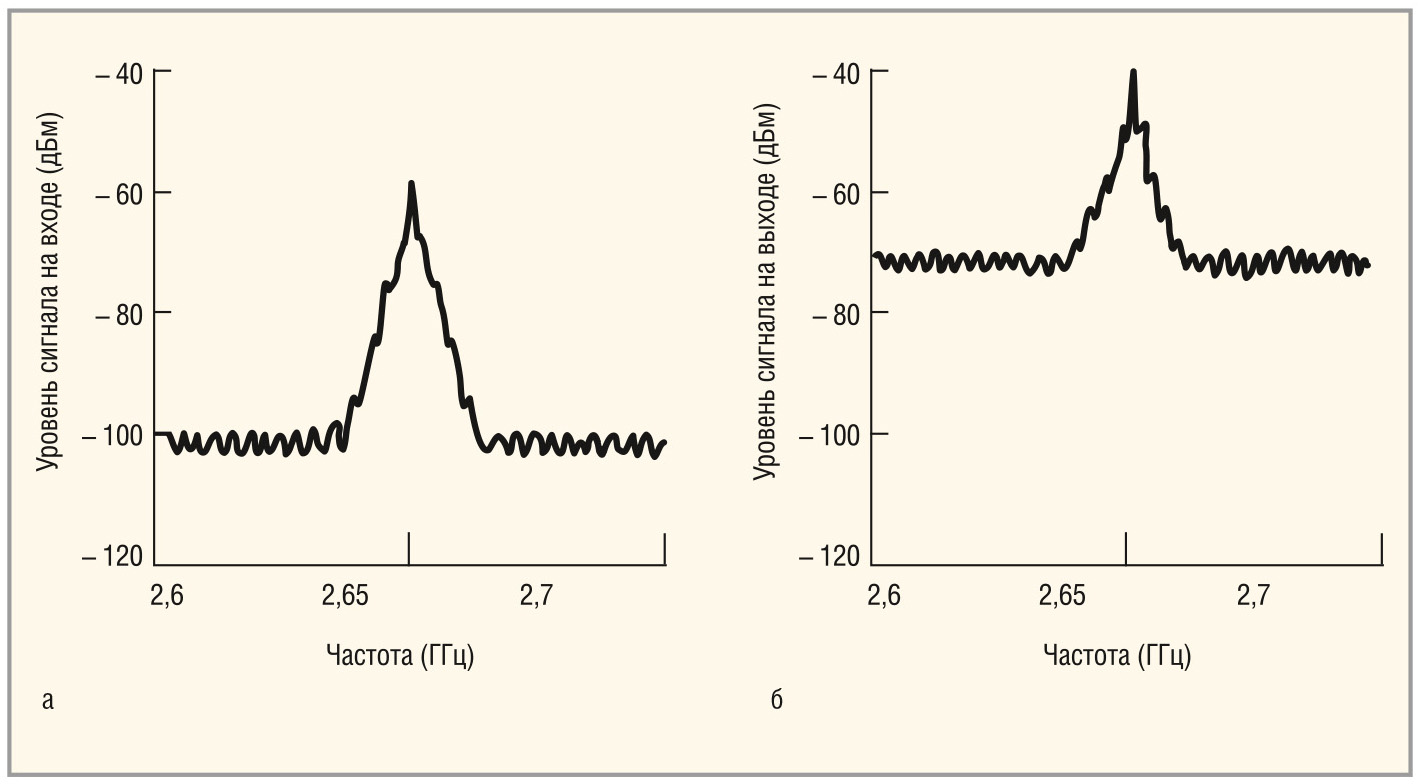
На рисунке 2 показан пример сигналов на входе и на выходе усилителя. Входной сигнал (см. рис. 2а) на 40 дБ превышает шумовой порог. Коэффициент передачи усилителя повысил уровень сигнала на 20 дБ (см. рис. 2б). Уровень входного шума также увеличился на 20 дБ, но при этом добавился собственный шум усилителя. Выходной сигнал стал только на 30 дБ выше шумового порога. Ухудшение отношения сигнал/шум на 10 дБ означает, что усилитель имеет коэффициент шума 10 дБ.

Обратите внимание: если бы уровень сигнала на входе был на 5 дБ ниже (то есть на 35 дБ выше шумового порога), на выходе он тоже оказался бы на 5 дБ ниже (на 25 дБ выше шумового порога), и коэффициент шума по-прежнему составлял бы 10 дБ. Таким образом, коэффициент шума не зависит от уровня входного сигнала.

Рассмотрим более тонкий эффект. Ухудшение отношения сигнал/шум в цепи зависит от температуры источника, который возбуждает цепь. Это можно доказать путём вычисления коэффициента шума F, где S_i и N_i – уровни сигнала и шума на входе тестируемого устройства; S_о и N_о – уровни сигнала и шума на выходе; N_а добавочный шум от устройства; G – коэффициент передачи.

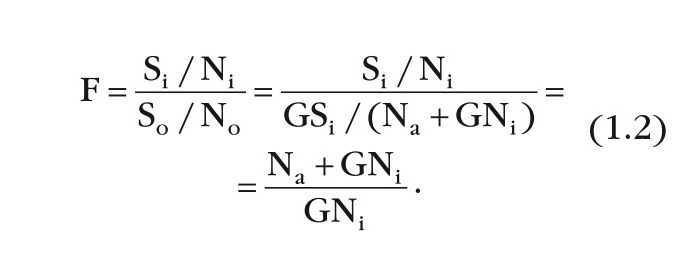
Уравнение (1.2) также может иметь вид:

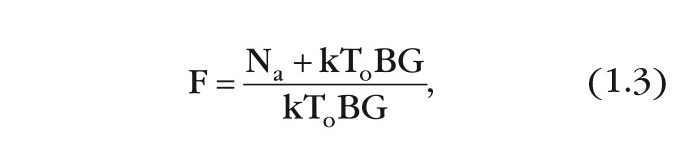
что является определением коэффициента шума, принятым IRE (предшественником IEEE).

В общем случае коэффициент шума является функцией частоты, но обычно не зависит от ширины полосы (пока полоса измерения достаточно узка, чтобы уловить вариации, происходящие при изменении частоты). Мощности шума N_а и N_i в уравнении (1.2) пропорциональны ширине полосы. Но ширина полосы в числителе равна таковой в знаменателе. Таким образом, коэффициент шума не зависит от ширины полосы.

Величину F часто называют «коэффициент шума» (Noise Figure), чаще – «шум-фактор» (Noise Factor) и иногда «коэффициент шума в линейных единицах» (Noise Figure in Linear Terms). В настоящее время термин «коэффициент шума» обычно используется для величины NF, измеряемой в децибелах, где:

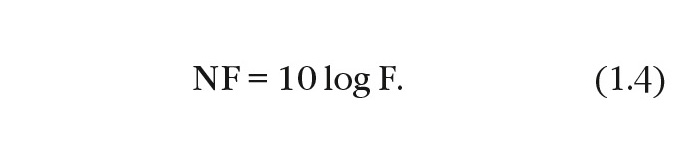
Далее в статье будет использоваться именно это обозначение.

Коэффициент шума и шумовая температура

Иногда для описания шумовых характеристик устройства вместо коэффициента шума (NF) используется «эффективная температура входного шума» T_е. Эта величина часто применяется для характеристики компонентов спутниковых приёмников. Величина Т_е соответствует температуре, которая создаёт мощность шума на выходе источника, подключённого к идеальному (бесшумовому) устройству, эквивалентную добавочному шуму N_a источника.

T_e определяется как:

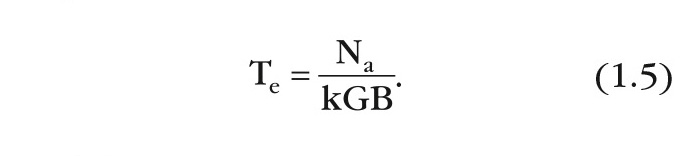
Эффективная температура входного шума связана с шум-фактором F следующим уравнением:

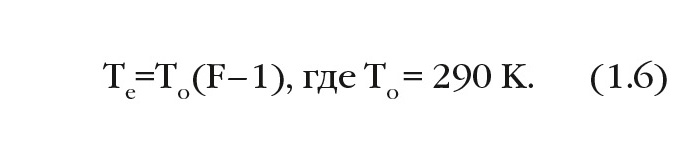
Температура входного шума в наземных СВЧ- и микроволновых системах связи обычно близка к опорной температуре 290 K – величине, используемой при вычислениях коэффициента шума, обусловленного температурой поверхности земли. В таком случае изменение коэффициента шума на 3 дБ будет приводить к изменению отношения сигнал/шум на те же 3 дБ.

Коэффициент шума многокаскадных систем

Определение коэффициента шума, рассмотренное вначале статьи, применимо как к отдельным компонентам (таким как, например, однотранзисторный усилитель), так и к готовым системам (например, приёмникам). Общий коэффициент шума системы можно вычислить, зная коэффициенты шума и коэффициенты передачи компонентов системы. Чтобы найти коэффициент шума каждого компонента, нужно определить шум N_a, добавляемый каждым каскадом. Коэффициент передачи тоже должен быть известен.

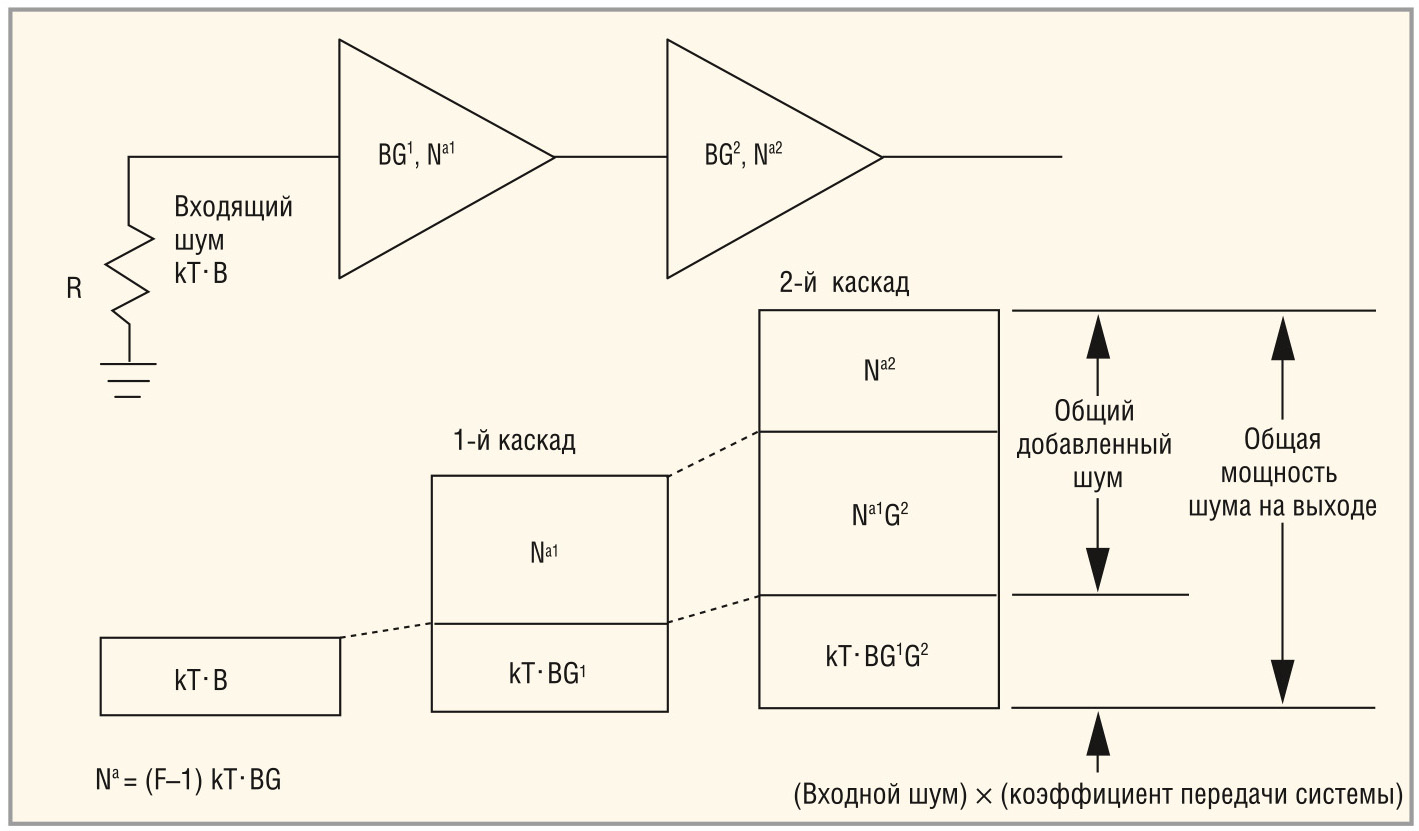
Для двухкаскадной системы (см. рис. 3) шум на выходе складывается из шума источника kT_oB, умноженного на общий коэффициент передачи системы G₁G₂, выходного шума первого усилителя N_a1, усиленного вторым каскадом G₂, и выходного шума второго усилителя N_a2. Вклады каскадов в мощность шума могут суммироваться, поскольку они не зависят друг от друга. Используя формулу (1.3) для шумовых вкладов усилителей, выходной шум можно выразить через их шум-факторы F:

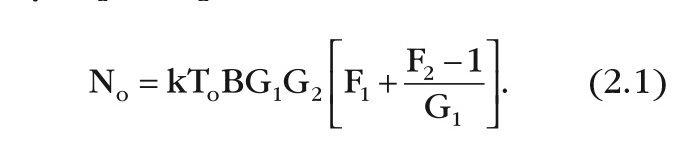
Зная шум на выходе, по формуле (1.1) можно вычислить шум-фактор систе­мы из двух усилителей. Для данного случая это и будет коэффициент шума системы.

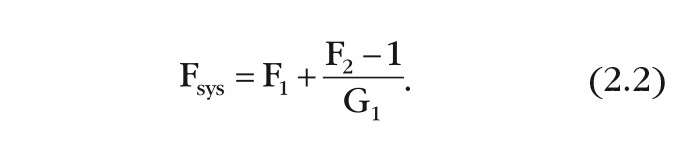
Величину [(F₂ – 1)/G₁] часто называют вкладом второго каскада. Можно заметить, что когда усиление на первом каскаде высоко, шумовой вклад второго каскада мал. Поэтому при создании приёмника так важен коэффициент передачи предусилителя. Если коэффициент передачи и общий шум-фактор системы известны, уравнение (2.2) можно переписать, чтобы найти F₁. По тому же принципу вычисляются показатели для n-каскадного устройства:

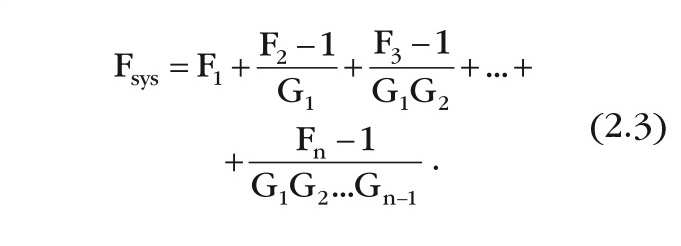
Уравнение (2.3) называют уравне­нием каскадного шума.

Коэффициент передачи и рассогласование

Коэффициент передачи устройства является важным параметром для вычисления шума. Используя в вычислениях значение входной мощности равное kT_oB, получаем номинальную мощность – максимум, который может быть достигнут на согласованной нагрузке. Если имеется большое рассогласование на входе устройства (что не редкость для малошумящих усилителей), фактическая мощность, поступающая в устройство, уменьшается. Если коэффициент передачи устройства определяется как отношение факти­ческой мощности, поступающей на нагрузку, к максимальной мощности, получаемой от источника, можно не учитывать потери рассогласования, присутствующие на входе устройства, поскольку они учитываются в коэффициенте передачи. Понимаемый таким образом коэффициент передачи называется коэффициентом передачи преобразователя (G_t). Однако при каскадном включении устройств ошибки рассогласования возрастают, если входной импеданс устройства отличается от импеданса нагрузки. В этом случае общий коэффициент передачи каскадно включённых устройств не равен произведению коэффициентов передачи отдельных каскадов.

Действительный коэффициент передачи (G_a), который часто указывается как параметр транзистора, представляет собой усиление, происходящее, когда заданная проводимость источника (Y_s) возбуждает устройство, а выход согласован с нагрузкой. Это часто используется при проектировании усилителей.

В качестве заданного или измеряемого коэффициента передачи в 50-омных системах наиболее часто используется вносимое усиление (G_i) или коэффициент прямой передачи (|S₂₁|²). Если измерительная система имеет малые коэффициенты отражения, а тестируемое устройство имеет хорошее согласование по выходу, применение уравнения для коэффициента шума каскадного включения (2.3) к реальным системам не даст большой ошибки. Если устройство имеет не очень хорошее согласование по выходу или у измерительной системы имеются существенные ошибки рассогласования, то между вычисленной характеристикой и характеристикой реальной системы появится расхождение. Например, если выходной импеданс первого каскада отличается от 50-омного импеданса источника, который используется при определении коэффициента шума второго каскада, шум, создаваемый во втором каскаде, может измениться.

Шумовые параметры

В принципе, коэффициент шума является упрощённой моделью реального шума в системе. Теоретически одиночный элемент шума присутствует в каждом каскаде. В большинстве реальных усилительных устройств, таких как транзисторы, имеются множественные шумы: тепловые, дробо­вые, шумы декомпозиции. Связь генерации этих шумов с импедансом источника может носить очень сложный характер. На результат измерения коэффициента шума влияют согласование источника шума и измерительного прибора с тестируемым устройством: источник шума создаёт импеданс на входе устройства, а устройство – на входе измерительного прибора. Фактическое значение коэффициента шума устройства, находящегося в рабочих условиях, зависит от согласованности с другими компонентами системы.

Разработка малошумящих усилителей требует компромисса между усилением каскада и его коэффициентом шума. Чтобы найти компромиссное решение, необходимо знать, как коэффициент передачи активного устройства и его коэффициент шума изменяются в зависимости от импеданса источника или его проводимости. Минимальный коэффициент шума не обязательно получается при импедансе системы (Z_o) или сопряжённом согласованном импедансе, при которых достигается максимальное усиление. Для полного понимания влияния рассогласования в системе необходимо знать две характеристики тестируемого устройства: коэффициент шума и коэффициент передачи.

Зависимость шум-фактора от импеданса источника, определяемая согласующим устройством, описывается уравнением:

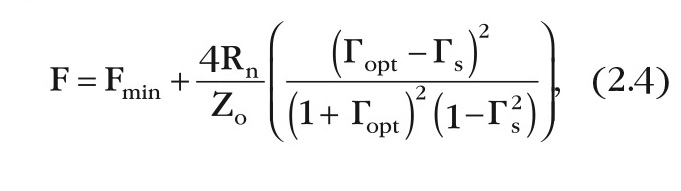
где Г – коэффициент отражения источника, имеющий результатом шум-фактор F, F_min – минимальный шум-фактор устройства, который имеет место когда Г = Г_opt, R_n – шумовое сопротивление (чувствительность коэффициента шума к изменению проводимости источника).

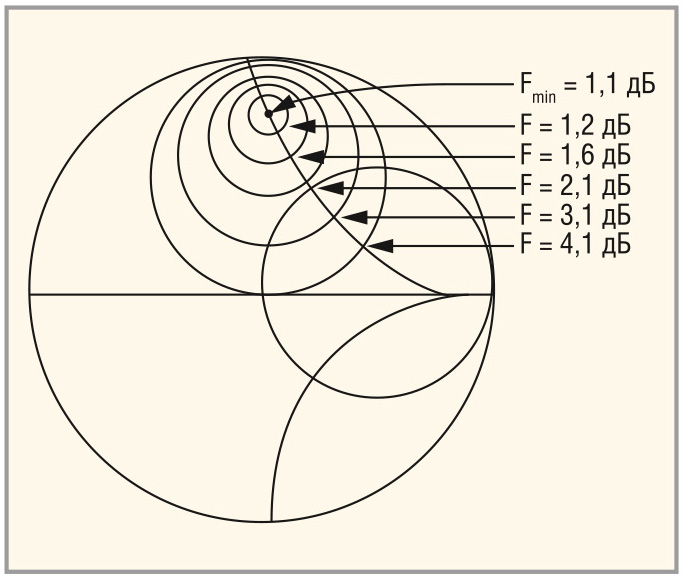
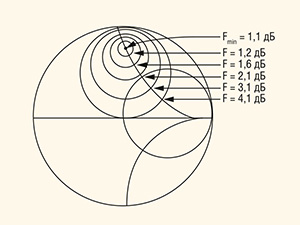
Об F_min, R_n и Г_opt часто говорят как о «шумовых параметрах», вместе они составляют понятие «шумовая характеристика» (Noise Characterization). На диаграмме Смита (см. рис. 4) коэффициент отражения источника (Г) для фиксированных значений шум-фактора изображается в виде круговых диаграмм шума (Noise Circles). Это удобный формат для отображения сложной зависимости между импедансом источника и коэффициентом шума.

Влияние ширины полосы

Несмотря на то, что ширина полосы частот является важным парамет­ром многих систем и используется в вычислениях фактического отношения сигнал/шум для демодулированных сигналов, коэффициент шума не зависит от ширины полосы устройства. При измерении шумов устройства принимается допущение о равномерности его амплитудно-частотной характеристики в пределах полосы измерения. Это означает, что ширина полосы измерения шума должна быть меньше ширины полосы устройства. Невыполнение этого условия приводит к ошибке измерения. Современные анализаторы коэффициента шума серии NFA компании Keysight имеют изменяемые полосы частот, что упрощает измерение узкополосных устройств, а также позволяет выполнять измерения на основе анализа спектра. Анализатор спектра серии PSA со специализированной программой измерения коэффициента шума имеет полосу пропускания, которая может быть уменьшена до 1 Гц.

Продолжение следует.

Литература

1. 10 Hints for Making Successful Noise Figure Measurements, Application Note 1341, lite­rature number 5980-0288E.
2. Noise Figure Measurement Accuracy, Appli­cation Note 57-1, literature number 5952-8255.
3. Noise Figure Measurement Accuracy, Appli­cation Note 57-2, literature number 5952-3706.
4. Calculate the Uncertainty of NF easurements Software and web-based tool available at: www.keysight.com/find/nfu
5. User guides for Keysight noise figure products available at: www.keysight.com/find/nf
6. Component Test web site: www.keysight.com/find/component_test
7. Spectrum analysis web sites: www.keysight.com/find/psa_personalities; www.keysight.com/find/esa_solutions

Если вам понравился материал, кликните значок - вы поможете нам узнать, каким статьям и новостям следует отдавать предпочтение. Если вы хотите обсудить материал - не стесняйтесь оставлять свои комментарии : возможно, они будут полезны другим нашим читателям!